实验测量

原子核由中子和质子构成。每个中子和质子都有自己的质量。但由于强相互作用与库伦相互作用的存在，一个原子核的质量不完全等于每个中子和质子的质量和。

比如氦原子的质量M( ( H e 2 4 ) {\displaystyle (He_{2}^{4})} )＝4.002603原子质量单位（u）,氢原子的质量M( ( H 1 1 ) {\displaystyle (H_{1}^{1})} )＝1.007825u,中子的质量M(n）＝1.008665u

氦核（ ( H e 2 4 ) {\displaystyle (He_{2}^{4})} ）的质量与组成它的2质子（即2个氢原子）与2个中子质量和不同：

2×M( ( H 1 1 ) {\displaystyle (H_{1}^{1})} )＋2×M（n）＝2×1.007825u＋2×1.008665u＝4.032980u

M（ ( H e 2 4 ) {\displaystyle (He_{2}^{4})} ）= 4.002603u

其差值为：

△M＝4.032980u－4.002603u＝0.030377u

当二个中子和二个质子组成一个氦核时，要损失△M＝0.030377u的质量。通过爱因斯坦的质能方程，可以算出由两个中子和两个质子形成一个氦核所释放的能量：ΔE＝ΔM ⋅ ⋅ --> {\displaystyle \cdot } c 2 {\displaystyle {c^{2}}} ＝28.30兆电子伏特。

原理

核结合能主要由强相互作用引起。其中包括体积能、表面能、库伦排斥能、对称能和对能等组成。

液滴模型

由于原子核的结构与水滴的结构十分相近，可将原子核近似看做密度十分巨大的液滴来处理，这就是原子核的液滴模型 。

结合能与比结合能

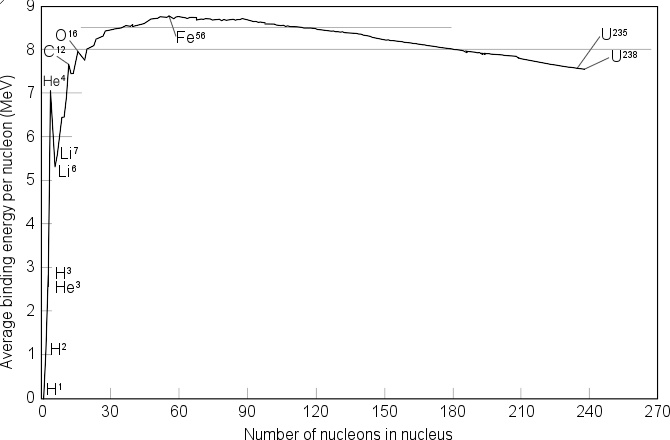
很显然，组成原子的核子越多，它的结合能就越高。因此，我们不妨将原子核的结合能与核子数之比定义为一个新的物理量—— 比结合能 （又称 平均结合能 ）。比结合能越大，原子核中的核子结合得越牢固，原子核越稳定。精密的物理检测表明对于质量数偏低的原子，核子比结合能随着质量数的增大而增大，而在镁和铁之间达到最大，之后便随着质量数的增大而减小。因此可以得出，当重原子裂变成两个或多个原子时，生成原子的结合能总和会大于原来重原子所具有的结合能，此间的差值便会以热能的形式释放出来，这便是核裂变反应。反之，当几个轻原子结合，合成原子的结合能大于原本所有原子结合能之和，这便是核聚变反应放出能量的来源。

应用

核能因为其巨大的能量具有强大的应用潜力但同时如果应用不当，落入反和平人士手中，其高强度能量却有可能变成全人类的灾难。核能一直备受抵制却不可替代。 核能的应用主要集中在以下几种形式：

核电站

医疗（放射性治疗）

小型核能动力装置

核武器

参见

国际原子能机构（IAEA）

核动力

核裂变

核聚变

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。