基础概念

定义

确定有限状态自动机 A {\displaystyle {\mathcal {A}}} 是由

一个非空有限的状态集合 Q {\displaystyle Q}

一个输入字母表 Σ Σ --> {\displaystyle \Sigma } （非空有限的字符集合）

一个转移函数 δ δ --> : Q × × --> Σ Σ --> → → --> Q {\displaystyle \delta :Q\times \Sigma \rightarrow Q} （例如： δ δ --> ( q , σ σ --> ) = p , ( p , q ∈ ∈ --> Q , σ σ --> ∈ ∈ --> Σ Σ --> ) {\displaystyle \delta \left(q,\sigma \right)=p,\left(p,q\in Q,\sigma \in \Sigma \right)} ）

一个开始状态 s ∈ ∈ --> Q {\displaystyle s\in Q}

一个接受状态的集合 F ⊆ ⊆ --> Q {\displaystyle F\subseteq Q}

所组成的5-元组。因此一个DFA可以写成这样的形式： A = ( Q , Σ Σ --> , δ δ --> , s , F ) {\displaystyle {\mathcal {A}}=\left(Q,\Sigma ,\delta ,s,F\right)} 。

工作方式（非正式的语义）

确定有限状态自动机从起始状态开始，一个字符接一个字符地读入一个字符串 w ∈ ∈ --> Σ Σ --> ∗ ∗ --> {\displaystyle w\in \Sigma ^{*}} （这里的 ∗ ∗ --> {\displaystyle {}^{*}} 指示Kleene星号算子。），并根据给定的转移函数一步一步地转移至下一个状态。在读完该字符串后，如果该自动机停在一个属于F的接受状态，那么它就接受该字符串，反之则拒绝该字符串。

扩展转移函数

为了在保证严谨的前提下，方便地叙述关于DFA的内容，我们定义如下扩展的转移函数：

δ δ --> ∗ ∗ --> ( q , w ) {\displaystyle \delta ^{*}\left(q,w\right)} 是自动机从状态q顺序读入字符串w后达到的状态

扩展转移函数递归的定义为：

工作方式（正式的语义）

对于一个确定有限状态自动机 A = ( Q , Σ Σ --> , δ δ --> , s , F ) {\displaystyle {\mathcal {A}}=\left(Q,\Sigma ,\delta ,s,F\right)} ，如果 δ δ --> ∗ ∗ --> ( s , w ) ∈ ∈ --> F {\displaystyle \delta ^{*}\left(s,w\right)\in F} ，我们就说该自动机接受字符串w，反之则表明该自动机拒绝字符串w。

被一个确定有限自动机接受的语言（或者叫“被识别的语言”）定义为： L ( A ) = { w ∈ ∈ --> Σ Σ --> ∗ ∗ --> | A {\displaystyle {\mathcal {L}}({\mathcal {A}})=\{w\in \Sigma ^{*}|{\mathcal {A}}~} 接受字符串 w } {\displaystyle ~w\}} ，也就是由所有被接受的字符串组成的集合。

DFA与有向图

除了数学上的严谨表述，通常为了讨论方便，也使用状态图直观地表示DFA。不难发现，对于一个给定的DFA，存在唯一一个对应的有向图（但是严格意义上一个有向图不能确定出唯一一个DFA）。有向图的每个结点对应一个状态，每条有向边对应一种转移。习惯上将结点画成两个圈表示接受状态，一个圈表示拒绝状态。用一条没有起点的边指向起始状态。

除了在表述上方便以外，在研究某些问题（如“给定的DFA的语言是否为无穷集合”）时，状态图也提供了有效的解法。

利弊

DFA是一种实际的计算模型，因为有平凡的线性时间、恒定空间的在线算法模拟在输入流上的DFA。给定两个DFA有有效算法找到识别它们所识别语言的并集、交集和补集的DFA。还有有效算法确定一个DFA是否接受任何给定字符串，一个DFA是否接受所有字符串，两个DFA是否识别同样的语言，和对特定正则语言找到状态数目最小的DFA（最小DFA）。

在另一方面，DFA在可识别的语言上有严格的限制—很多简单的语言，包括需要多于恒定空间来解决的任何问题，不能被DFA识别。经典的DFA不能识别的简单语言的例子是括号语言，就是由正确配对的括号组成的语言，比如 (()())。由形如 a b 的字符串组成的语言，就是有限数目个a，随后是相等数目个b。可以证明没有DFA有足够状态来识别这种语言（通俗地说，因为需要至少2n个状态，而n是不恒定的）。

其它

能被确定有限状态自动机识别的语言是正则语言。

确定有限状态自动机是非确定有限状态自动机的一种极限形式。

确定有限状态自动机在计算能力上等价于非确定有限状态自动机。

没有接受状态列表并没有指定开始状态的确定有限状态机叫做转移系统或半自动机。

例子

下面是一个确定有限状态自动机的例子。

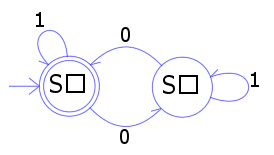
A {\displaystyle {\mathcal {A}}} 的状态图

确定有限状态自动机 A = ( Q , Σ Σ --> , δ δ --> , s , F ) {\displaystyle {\mathcal {A}}=\left(Q,\Sigma ,\delta ,s,F\right)}

Q = { S 1 , S 2 } {\displaystyle Q=\{S_{1},S_{2}\}}

Σ Σ --> = { 0 , 1 } {\displaystyle \Sigma =\{0,1\}}

s = S 1 {\displaystyle s=S_{1}}

F = { S 1 } {\displaystyle F=\{S_{1}\}}

δ δ --> {\displaystyle \delta } 由下面的状态转移表定义：

对应的转移函数为：

状态 S 1 {\displaystyle S_{1}} 表示在输入的字符串中有偶数个0，而 S 2 {\displaystyle S_{2}} 表示有奇数个0。在输入中1不改变自动机的状态。当读完输入的字符串的时候，状态将显示输入的字符串是否包含偶数个0。

A {\displaystyle {\mathcal {A}}} 能识别的的语言是 L ( A ) = { w | # # --> 0 ( w ) ≡ ≡ --> 0 ( m o d 2 ) } {\displaystyle {\mathcal {L}}({\mathcal {A}})=\{w|\#_{0}(w)\equiv 0~(mod~2)\}} 。用正则表达式表示为： ( 1 ∗ ∗ --> ( 01 ∗ ∗ --> 0 ) ∗ ∗ --> ) ∗ ∗ --> {\displaystyle (1^{*}(01^{*}0)^{*})^{*}} 。

封闭性及一些运算

封闭性

确定有限状态自动机的交，并，差，补，连接，替换，同态，逆同态等运算是封闭的，也就是说确定有限状态自动机通过这些运算产生的新的自动机也是确定有限状态自动机。

补运算

A = ( Q , Σ Σ --> , δ δ --> , s , F ) {\displaystyle {\mathcal {A}}=(Q,\Sigma ,\delta ,s,F)} 是一个DFA，那么由补运算产生的新DFA定义为： A ¯ ¯ --> = ( Q , Σ Σ --> , δ δ --> , s , Q − − --> F ) {\displaystyle {\bar {\mathcal {A}}}=(Q,\Sigma ,\delta ,s,Q-F)} 。显然只要将 A {\displaystyle {\mathcal {A}}} 中接受的状态设为不接受的状态，同时把不接受的状态设为接受的状态就得到 A ¯ ¯ --> {\displaystyle {\bar {\mathcal {A}}}} 。补运算的复杂度是： O ( | Q | ) {\displaystyle O(\left|Q\right|)} 。

交运算和并运算

有两个DFA， A 1 = ( Q 1 , Σ Σ --> , δ δ --> 1 , s 1 , F 1 ) {\displaystyle {\mathcal {A}}_{1}=(Q_{1},\Sigma ,\delta _{1},s_{1},F_{1})} 和 A 2 = ( Q 2 , Σ Σ --> , δ δ --> 2 , s 2 , F 2 ) {\displaystyle {\mathcal {A}}_{2}=(Q_{2},\Sigma ,\delta _{2},s_{2},F_{2})} ，那么由这两个DFA创造出来的新的自动机定义为： B = ( Q 1 × × --> Q 2 , Σ Σ --> , δ δ --> B , ( s 1 , s 2 ) , M ) {\displaystyle {\mathcal {B}}=(Q_{1}\times Q_{2},\Sigma ,\delta _{\mathcal {B}},(s_{1},s_{2}),M)} 。其中 M ⊆ ⊆ --> Q 1 × × --> Q 2 {\displaystyle M\subseteq Q_{1}\times Q_{2}} ， ( s 1 , s 2 ) {\displaystyle \left(s_{1},s_{2}\right)} 为 B {\displaystyle {\mathcal {B}}} 的开始状态， δ δ --> B {\displaystyle \delta _{\mathcal {B}}} 为 B {\displaystyle {\mathcal {B}}} 的转移函数，且作如下定义： ∀ ∀ --> q 1 ∈ ∈ --> Q 1 , q 2 ∈ ∈ --> Q 2 , σ σ --> ∈ ∈ --> Σ Σ --> : δ δ --> B ( ( q 1 , q 2 ) , σ σ --> ) = ( δ δ --> 1 ( q 1 , σ σ --> ) , δ δ --> 2 ( q 2 , σ σ --> ) ) {\displaystyle \forall q_{1}\in Q_{1},~q_{2}\in Q_{2},~\sigma \in \Sigma :\delta _{\mathcal {B}}((q_{1},q_{2}),\sigma )=(\delta _{1}(q_{1},\sigma ),\delta _{2}(q_{2},\sigma ))} 。

当 M = F 1 × × --> F 2 {\displaystyle M=F_{1}\times F_{2}} 时，由上述方法得到的 B {\displaystyle {\mathcal {B}}} 就是DFA A 1 {\displaystyle {\mathcal {A}}_{1}} 和 A 2 {\displaystyle {\mathcal {A}}_{2}} 的交运算，记作： B = A 1 ∩ ∩ --> A 2 {\displaystyle {\mathcal {B}}={\mathcal {A}}_{1}\cap {\mathcal {A}}_{2}} 。也就是说对于读入的字符串w，当且仅当 A 1 {\displaystyle {\mathcal {A}}_{1}} 和 A 2 {\displaystyle {\mathcal {A}}_{2}} 同时接受w的时候 B {\displaystyle {\mathcal {B}}} 接受w。

当 M = Q 1 × × --> F 2 ⋃ ⋃ --> F 1 × × --> Q 2 {\displaystyle M=Q_{1}\times F_{2}\bigcup F_{1}\times Q_{2}} 时，由上述方法得到的 B {\displaystyle {\mathcal {B}}} 就是DFA A 1 {\displaystyle {\mathcal {A}}_{1}} 和 A 2 {\displaystyle {\mathcal {A}}_{2}} 的并运算，记作： B = A 1 ∪ ∪ --> A 2 {\displaystyle {\mathcal {B}}={\mathcal {A}}_{1}\cup {\mathcal {A}}_{2}} 。也就是说对于读入的字符串w，只要 A 1 {\displaystyle {\mathcal {A}}_{1}} 或 A 2 {\displaystyle {\mathcal {A}}_{2}} 中至少有一个接受w， B {\displaystyle {\mathcal {B}}} 就接受w。

交运算和并运算的复杂度都是 O ( | Q 1 | | Q 2 | | Σ Σ --> | ) {\displaystyle O(\left|Q_{1}\right|\left|Q_{2}\right|\left|\Sigma \right|)} 。

同态和逆同态运算

一个同态函数 h : Σ Σ --> ∗ ∗ --> → → --> Γ Γ --> ∗ ∗ --> {\displaystyle h:\Sigma ^{*}\rightarrow \Gamma ^{*}} 可以递归的定义为：

h ( ϵ ϵ --> ) = ϵ ϵ --> {\displaystyle ~h(\epsilon )=\epsilon }

h ( u σ σ --> ) = h ( u ) h ( σ σ --> ) {\displaystyle ~h(u\sigma )=h(u)h(\sigma )}

于是则有 h ( u v ) = h ( u ) h ( v ) {\displaystyle ~h(uv)=h(u)h(v)} 。（以上所述中 ϵ ϵ --> {\displaystyle ~\epsilon } 为空字符， u , v ∈ ∈ --> Σ Σ --> ∗ ∗ --> , σ σ --> ∈ ∈ --> Σ Σ --> {\displaystyle ~u,v\in \Sigma ^{*},\sigma \in \Sigma } ）

L ⊆ ⊆ --> Σ Σ --> ∗ ∗ --> : h ( L ) := { h ( w ) | w ∈ ∈ --> L } {\displaystyle {\mathcal {L}}\subseteq \Sigma ^{*}:h({\mathcal {L}}):=\{h(w)~|~w\in {\mathcal {L}}\}} ：对于接受语言L的DFA，只要将其中代表 δ δ --> ( q , σ σ --> ) {\displaystyle ~\delta (q,\sigma )} 的边替换成一个序列 h ( σ σ --> ) {\displaystyle ~h(\sigma )} 并在其中加入不属于原DFA状态的新状态，就产生了接受语言h(L)的DFA。

L ⊆ ⊆ --> Γ Γ --> ∗ ∗ --> : h − − --> 1 ( L ) := { w | h ( w ) ∈ ∈ --> L } {\displaystyle {\mathcal {L}}\subseteq \Gamma ^{*}:h^{-1}({\mathcal {L}}):=\{w~|~h(w)\in {\mathcal {L}}\}} ：定义一个 Q , Σ Σ --> , s , F {\displaystyle ~Q,\Sigma ,s,F} 都不变的新DFA，并定义新的转移函数为 δ δ --> ′ ( q , σ σ --> ) := δ δ --> ∗ ∗ --> ( q , h ( σ σ --> ) ) {\displaystyle ~\delta "(q,\sigma ):=\delta ^{*}(q,h(\sigma ))} ，则 ( Q , Σ Σ --> , δ δ --> ′ , s , F ) {\displaystyle ~(Q,\Sigma ,\delta ",s,F)} 就是逆同态运算产生的新DFA。

此外替换运算和逆同态运算的方法近似。

最小自动机

等价类自动机

对于一个正则语言，接受该语言的等价类自动机是一个 ( Q , Σ Σ --> , δ δ --> , s , F ) {\displaystyle ~(Q,\Sigma ,\delta ,s,F)} 的5-元组。其定义如下：

Q是等价关系~ L 的等价类的集合： [ x ] , x ∈ ∈ --> Σ Σ --> ∗ ∗ --> {\displaystyle [x],x\in \Sigma ^{*}} 的集合

s = [ ϵ ϵ --> ] {\displaystyle ~s=[\epsilon ]}

F = { [ x ] | x ∈ ∈ --> L } {\displaystyle F=\{[x]~|~x\in L\}}

δ δ --> ( [ x ] , σ σ --> ) = [ x σ σ --> ] {\displaystyle ~\delta ([x],\sigma )=[x\sigma ]}

~ L 被称为Nerode关系，是Myhill-Nerode定理的基础。简单的来说就是对于任意 x , y , z ∈ ∈ --> Σ Σ --> ∗ ∗ --> {\displaystyle ~x,y,z\in \Sigma ^{*}} ，如果 x z ∈ ∈ --> L ⇔ ⇔ --> y z ∈ ∈ --> L {\displaystyle xz\in L\Leftrightarrow yz\in L} ，那么x~ L y。

唯一性

对于任意给定的确定有限状态自动机都能找到一个与之计算能力等价的最小确定有限状态自动机，简称最小自动机。该最小自动机中状态的数量等于能识别相同语言的等价类自动机中等价关系的数量，我们可以称最小自动机和等价类自动机“实际上”是相等的，也就是同构。非正式的说法是：对于最小自动机上的任意状态都可以通过一个同构函数变换成等价类自动机上的一个状态。

能识别一个正则语言的等价类自动机是唯一的，因此能识别该语言的最小自动机也是唯一的。

算法

定义一个非等价关系： N := { ( p , q ) | p , q ∈ ∈ --> Q , ∃ ∃ --> w ∈ ∈ --> Σ Σ --> ∗ ∗ --> : δ δ --> ∗ ∗ --> ( p , w ) ∈ ∈ --> F ↔ ↔ --> δ δ --> ∗ ∗ --> ( q , w ) ∉ ∉ --> F } {\displaystyle N:=\{(p,q)~|~p,q\in Q,\exists w\in \Sigma ^{*}:\delta ^{*}(p,w)\in F\leftrightarrow \delta ^{*}(q,w)\notin F\}} ，如下步骤可以得到这个集合N：

如果 p ∈ ∈ --> F , q ∉ ∉ --> F {\displaystyle p\in F,~q\notin F} ，就给所有的状态对(p,q)和(q,p)打上标记

重复步骤3，直到所标记的状态对没有变化为止

对于未标记的状态对(p,q)和σ，如果 ( δ δ --> ( p , σ σ --> ) , δ δ --> ( q , σ σ --> ) ) {\displaystyle ~(\delta (p,\sigma ),\delta (q,\sigma ))} 被标记过了就把(p,q)也标记上

以上所有标记了的状态对的集合就是非等价关系N

以下是由一个任意DFA转换到一个最小DFA的步骤：

把所有不能从开始状态达到的状态删除

通过上述标记算法计算非等价关系N

一步一步将不属于N的状态对中的两个状态合成一个状态

这样就得到了接受相同语言的最小自动机。复杂度为 O ( | Q | 2 | Σ Σ --> | ) {\displaystyle O(\left|Q\right|^{2}\left|\Sigma \right|)} 。

引用

Michael Sipser, Introduction to the Theory of Computation . PWS, Boston. 1997. ISBN 0-534-94728-X. Section 1.1: Finite Automata, pp.31–47. Subsection "Decidable Problems Concerning Regular Languages" of section 4.1: Decidable Languages, pp.152–155.4.4 DFA can accept only regular language

参见

无环确定有限状态自动机

非确定有限状态自动机

图灵机

读只右移图灵机

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。