定义

对于不同的流场，雷诺数可以有很多表达方式。这些表达方式一般都包括流体性质（密度、黏度）再加上流体速度和一个特征长度或者特征尺寸。这个尺寸一般是根据习惯定义的。比如说半径和直径对于球型和圆形并没有本质不同，但是习惯上只用其中一个。对于管内流动和在流场中的球体，通常使用直径作为特征尺寸。对于表面流动，通常使用长度。

管内流场

对于在管内的流动，雷诺数定义为：

式中：

V {\displaystyle {\mathbf {\mathrm {V} }}} 是平均流速（国际单位：m/s）

D {\displaystyle {D}} 管直径（一般为特征长度）(m)

μ μ --> {\displaystyle {\mu }} 流体动力黏度（Pa·s或N·s/m²）

ν ν --> {\displaystyle {\nu }} 运动黏度（ ν ν --> = μ μ --> / {\displaystyle \nu =\mu /} ρ ）(m²/s)

ρ ρ --> {\displaystyle {\rho }} 流体密度（kg/m³）

Q {\displaystyle {Q}} 体积流量（m³/s）

A {\displaystyle {A}} 横截面积（m²）

假如雷诺数的体积流速固定，则雷诺数与密度（ρ）、速度的开方（ u {\displaystyle {\sqrt {u}}} ）成正比；与管径（Ｄ）和黏度（ｕ）成反比

假如雷诺数的质量流速（即是可以稳定流动）固定，则雷诺数与管径（Ｄ）、黏度（ｕ）成反比；与√速度（ u {\displaystyle {\sqrt {u}}} ）成正比；与密度（ρ）无关

平板流

对于在两个宽板(板宽远大于两板之间距离)之间的流动,特征长度为两倍的两板之间距离。

流体中的物体

对于流体中的物体的雷诺数,经常用 Re p 表示。用雷诺数可以研究物体周围的流动情况，是否有漩涡分离，还可以研究沉降速度。

流体中的球

对于在流体中的球，特征长度就是这个球的直径，特征速度是这个球相对于远处流体的速度，密度和黏度都是流体的性质。在这种情况下，层流只存在于Re=10或者以下。 在小雷诺数情况下，力和运动速度的关系遵从斯托克斯定律。

搅拌槽

对于一个圆柱形的搅拌槽，中间有一个旋转的桨或者涡轮，特征长度是这个旋转物体的直径。速度是ND,N是转速(周/秒)。雷诺数表达为:

当Re>10,000时，这个系统为完全湍流状态。

过渡流雷诺数

对于流过平板的边界层，实验可以确认，当流过一定长度后,层流变得不稳定形成湍流。对于不同的尺度和不同的流体，这种不稳定性都会发生。一般来说，当 R e x ≈ ≈ --> 5 × × --> 10 5 {\displaystyle \mathrm {Re} _{x}\approx 5\times 10^{5}} , 这里x是从平板的前边缘开始的距离,流速是自由层以外的自由流场速度。

一般管道流雷诺数＜2100为层流(又可称作黏滞流动、线流)状态，大于4000为湍流(又可称作紊流、扰流)状态，2100～4000为过渡流状态。

层流：流体沿着管轴以平行方向流动，因为流体很平稳，所以可看作层层相叠，各层间不互相干扰。流体在管内速度分布为抛物体的形状，面向切面的则是抛物线分布。因为是个别有其方向和速率流动，所以流动摩擦损失较小。

湍流：此则是管内流体流动状态为各分子互相激烈碰撞，非直线流动而是漩涡状，流动摩擦损失较大。

管道中的摩擦阻力

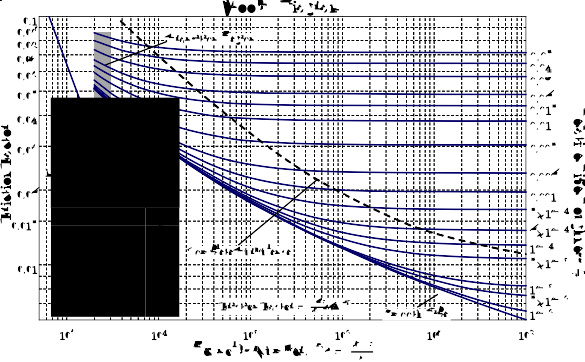
 穆迪图说明达西摩擦因子 f 和雷诺数和相对粗糙度的关系

在管道中完全成形（fully developed）流体的压降可以用穆迪图来说明，穆迪图绘制出在不同相对粗糙度下，达西摩擦因子 f 和雷诺数 R e {\displaystyle {\mathrm {Re} }} 及相对粗糙度 ϵ ϵ --> / D {\displaystyle \epsilon /D} 的关系，图中随着雷诺数的增加，管流由层流变为过渡流及湍流，管流的特性和流体为层流、过渡流或湍流有明显关系。

流动相似性

两个流动如果相似的话，他们必须有相同的几何形状和相同的雷诺数和欧拉数。当在模型和真实的流动之间比较两个流体中相应的一点，如下关系式成立：

带m下标的表示模型里的量，其他的表示实际流动里的量。 这样工程师们就可以用缩小尺寸的水槽或者风洞来进行试验，与数值模拟的模型比对数据分析，节约试验成本和时间。实际应用中也许会需要其他的无量纲量与模型一致，比如说马赫数，福禄数。

雷诺数的一般值

精子~ 1×10

大脑中的血液流 ～1×10

主动脉中的血流~ 1×10

湍流临界值 ~ 2.3×10 -5.0×10 (对于管内流)到10 (边界层)

棒球（职业棒球投手投掷）~2×10

游泳（人）~4×10

蓝鲸~ 3×10

大型邮轮~ 5×10

雷诺数的推导

雷诺数可以从无量纲的非可压纳维－斯托克斯方程推导得来:

上式中每一项的单位都是加速度乘以密度。无量纲化上式，需要把方程变成一个独立于物理单位的方程。我们可以把上式乘以系数:

这里的字母跟在雷诺数定义中使用的是一样的。我们设:

无量纲的纳维-斯托克斯方程可以写为:

这里: μ μ --> ρ ρ --> D V = 1 R e . {\displaystyle {\frac {\mu }{\rho DV}}={\frac {1}{\mathit {Re}}}.}

最后,为了阅读方便把撇去掉:

这就是为什么在数学上所有的具有相同雷诺数的流场是相似的。

参见

磁雷诺数

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。