历史

在新的实验技巧发现出许多粒子后，开发分类方案便成了一个及时的问题，因为不可能这么多粒子全都是基本粒子。这些发现使得沃尔夫冈·泡利惊呼：“要是早知道会这样，我就从事植物学研究算了”，而恩里科·费米则对学生利昂·莱德曼说：“年轻人呀，如果我能记住所有粒子的名字，那么我就是植物学家了。”这些新的实验方案为实验物理学家们赢得了诺贝尔奖，当中包括在这些许多开发前端的路易斯·阿尔瓦雷茨。用较少的构成物来把强子构建成束缚态就可以把手上的“动物园”妥当编组。之前的几个提案，例如恩里科·费米和杨振宁的（1949年），还有坂田昌一的 坂田模型 （ 英语 ： Sakata model ） （1956年），都能够让人满意地将介子分类，但却无法应付重子，因此并不能解释所有实验数据。

由默里·盖尔曼和西岛和彦所提出的盖尔曼-西岛关系，使得盖尔曼发明了八重道的分类，当中还包括了 尤瓦勒·内埃曼 （ 英语 ： Yuval Ne"eman ） 于1961年的独立重要贡献。强子分为SU(3)表示多重态、八重态和十重态，由于强相互作用的关系，所以各态中的强子质量大致相同。 盖尔曼-大久保质量公式 （ 英语 ： Gell-Mann–Okubo mass formula ） 将强子多重态中各粒子细小的质量差异定量，由SU(3)的明显对称性破缺所控制。

十重态中自旋为 ⁄ 2 Ω − 重子是该分组的重要预测。在布鲁克黑文国家实验室发现了它之后，盖尔曼于1969年因八重道的研究而获颁诺贝尔物理学奖。

盖尔曼和独立的乔治·茨威格最终在1964年辨识出八重道所隐藏的。他们假定了基本费米子构成物的存在，它当时尚未被观测到，可能以后都不会看到它的自由形态，而它用一种既经济又紧密的方式优雅地了编写了八重道的基础，使强子分类变得更加简单。当时强子的质量差异被视为是组夸克质量的结果。

人类在此之后还花了十年才对这些夸克意想不到的性质——和物理现实（见夸克）——更加地了解。它们违反直觉地永远不能被分开观测（夸克禁闭），但它们一直与其他夸克结合来形成整套强子，然后向外界提供大量关于被囚夸克本身的信息。相反地，夸克在量子色动力学中扮演着定义的角色，量子色动力学是负责完全描述强相互作用的理论；而八重道现在则被理解成由最轻的三种夸克味对称结构的结果。

介子

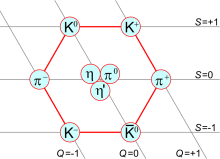
  图二：自旋为0的伪标量介子所形成的九重态。

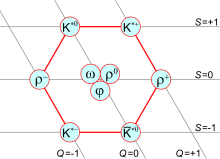
  图三：自旋为1的介子所形成的九重态。

八重道分类的是以以下的事实来命名。如果取三种夸克，那么夸克所处的 基本表示 （ 英语 ： Fundamental representation ） 就是SU(3)味对称的 3 （叫三重态）。而反夸克所处的则是复共轭表示 3 。这九个态（九重态）可被分离成平凡表示 1 （单态），以及伴随表示 8 （八重态）。这项分解可被写成：

图一所示的就是上述分解对介子的应用。若味对称是精确的话（限制在只有强相互作用的情况下，在概念上把弱相互作用关掉），则它们的重量应该是一样的。完整理论的物理内容包括由夸克质量差异所造成的对称破缺考量，还有把各种多重态（例如八重态和单态）混合的考量。

但是要注意的是，η与η"间的质谱分裂比夸克模型能接受的要大，而这个“η-η"难题”源自强相互作用真空态的各种特性，例如瞬子结构。

介子是重子数为零的强子。若夸克－反夸克对的角动量态为 L ，自旋为 S ，则

∣ ∣ --> L − − --> S ∣ ∣ -->⩽ ⩽ --> J ⩽ ⩽ --> L + S {\displaystyle \mid L-S\mid \leqslant J\leqslant L+S} ，其中 S =0或1，

P = ( − − --> 1 ) L + 1 {\displaystyle P=(-1)^{L+1}} ，其中指数中的1是来自夸克－反夸克对的 内在宇称 （ 英语 ： Intrinsic parity ） 。

无味介子的 C = ( − − --> 1 ) L + S {\displaystyle C=(-1)^{L+S}} ，有味介子的 C 则不一定。

对同位旋 I =1或0的态而言，可定义一个叫 G宇称 （ 英语 ： G-parity ） 的 乘法量子数 （ 英语 ： Multiplicative quantum number ） G = ( − − --> 1 ) I + L + S {\displaystyle G=(-1)^{I+L+S}} 。

若 P = ( − − --> 1 ) J {\displaystyle P=(-1)^{J}} ，于是S=1，因此 P C = 1 {\displaystyle PC=1} 。拥有这称组合的量子态叫自然宇称态，其他组合的量子态则叫奇异量子态（例如 J P C = 0 − − --> − − --> {\displaystyle J^{PC}=0^{--}} 态）。

重子

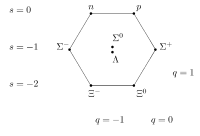
  图四：自旋为 ⁄ 2 的重子所形成的八重态。

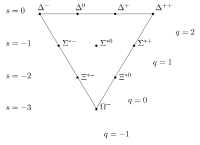
  图五：自旋为 ⁄ 2 的重子所形成的十重态。

由于夸克是费米子，所以根据自旋统计定理在任二夸克的交换下波函数必为反对称。反对称的波函数可经由把所有色设为完全反对称（见下文）但味、自旋及空间皆对称的情况下得出。三种味时的味分解如下：

第一项是味对称（以S表示）的十重态，第二及第三项都是味混合（以M表示）的八重态，最后的是反对称（以A表示）的单态。态的空间和自旋部分有混合，因此得出轨道角动量需立即处理。

有些时候改用夸克基态空间来思考会更有用，三种味各两种自旋，总数为六态。这种近似对称叫SU(6)自旋－味对称。按照此群的分解如下：

56种自旋－味的对称组合可在SU(3)味对称下分解为：

其中上标为重子的自旋 S 。由于这些态的自旋和味皆对称，因此它们在空间上也应该对称——这个条件能透过把轨道角动量 L 定为0来轻易满足。它们都是基态重子。

第二项 S = ⁄ 2 的重子八重态共有两种核子（ p + 、 n 0 ）、三种Σ粒子（ Σ + 、 Σ 0 、 Σ − ）、两种Ξ粒子（ Ξ 0 , Ξ − ），以及Λ粒子（ Λ 0 ）。而第一项 S = ⁄ 2 的重子十重态共有四种Δ粒子（ Δ ++ 、 Δ + 、 Δ 0 、 Δ − ）、三种Σ粒子（ Σ ∗+ , Σ ∗0 , Σ ∗− ）、两种Ξ粒子（ Ξ ∗0 , Ξ ∗− ），以及Ω粒子（ Ω − ）。

这个模型成功解决的问题还包括重子的混合、多重态内或之间的质谱分裂，以及磁矩。

色荷的发现

色量子数是强相互作用特有的量子数，它们与弱电相互作用完全没有关系。在了解到自旋S为 ⁄ 2 的[[Δ粒子|Δ }}需要三个自旋相同的上夸克和零轨道角动量之后，色荷的发现就成了夸克模型分类的结果。这是因为它的波函数不可能是不对称的（这是由于泡利不相容原理之故），除非还有隐藏的量子数。 奥斯卡·格林伯格 （ 英语 ： Oscar W. Greenberg ） 于1964年注意到这个问题，并提出夸克应该是 仲费米子 （ 英语 ： Parastatistics ） 。

韩武荣和南部阳一郎在六个月之后提出另一替代方案，若存在三个夸克三重态就能解决这个问题，但是由于这样色和味不存在对易关系，因此两者会缠绕在一起 。

完全与其他荷对易并且带强相互作用荷的色荷现代概念是由 威廉·巴丁 （ 英语 ： William A. Bardeen ） 、哈拉尔德·弗里奇和默里·盖尔曼于1973年构思出来 。

夸克模型以外的态

虽然夸克模型可由量子色动力学理论中推导出来，但是强子的结构却比模型所能容许的要复杂得多。所有强子的完全量子力学波函数必须包括虚夸克对和虚胶子对，同时亦要容许多种混合。可能有强子位处夸克模型之外。这样的粒子包括胶球（只含有价胶子）、混合粒子（含有价胶子和夸克）和“奇异强子”（包括四夸克态和五夸克态）。

延伸阅读

S. Eidelman et al. Particle Data Group.Review of Particle Physics (PDF) . Physics Letters B. 2004, 592 : 1. arXiv:astro-ph/0406663 .Bibcode:2004PhLB..592....1P. doi:10.1016/j.physletb.2004.06.001 .

Lichtenberg, D B. Unitary Symmetry and Elementary Particles. Academic Press. 1970. ISBN 978-1483242729.

J.J.J. Kokkedee. The quark model. W. A. Benjamin. 1969. ASIN B001RAVDIA .

另见

次原子粒子

强子、介子、重子和夸克

奇异强子：奇异重子

量子色动力学和味 (粒子物理学)

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。