原理

关于这部分的详细内容，请参见主条目：衍射。

通常所讲的衍射光栅是基于夫琅禾费多缝衍射效应工作的。描述光栅结构与光的入射角和衍射角之间关系的公式叫“光栅方程”。

波在传播时，波阵面上的每个点都可以被认为是一个单独的次波源；这些次波源再发出球面次波，则以后某一时刻的波阵面，就是该时刻这些球面次波的包络面（惠更斯原理）。

一个理想的衍射光栅可以认为由一组等间距的无限长无限窄狭缝组成，狭缝之间的间距为d，称为光栅常数。当波长为λ的平面波垂直入射于光栅时，每条狭缝上的点都扮演了次波源的角色；从这些次波源发出的光线沿所有方向传播（即球面波）。由于狭缝为无限长，可以只考虑与狭缝垂直的平面上的情况，即把狭缝简化为该平面上的一排点。则在该平面上沿某一特定方向的光场是由从每条狭缝出射的光相干叠加而成的。在发生干涉时，由于从每条狭缝出射的光的在干涉点的相位都不同，它们之间会部分或全部抵消。然而，当从相邻两条狭缝出射的光线到达干涉点的光程差是光的波长的整数倍时，两束光线相位相同，就会发生干涉加强现象。以公式来描述，当衍射角θm满足关系dsinθm/λ=|m|时发生干涉加强现象，这里d为狭缝间距，即光栅常数，m是一个整数，取值为0，±1，±2，……。这种干涉加强点称为衍射极大。因此，衍射光将在衍射角为θm时取得极大，即：

上式即为光栅方程。当平面波以入射角θi入射时，光栅方程写为

衍射光栅强度分布

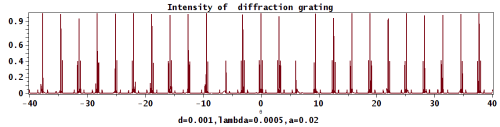
衍射光栅的强度分布（电脑模拟）

衍射光栅 电脑模拟

衍射光栅的强度分布是衍射因子和干涉因子的乘积：

P=D(θ θ -->)∗ ∗ -->I(θ θ -->){\displaystyle P=D(\theta )*I(\theta )}

其中 D 是 衍射因子

D=sin⁡ ⁡ -->(π π -->∗ ∗ -->d∗ ∗ -->sin⁡ ⁡ -->(θ θ -->)/λ λ -->)2∗ ∗ -->λ λ -->2(π π -->2∗ ∗ -->d2∗ ∗ -->sin⁡ ⁡ -->(θ θ -->)2){\displaystyle D={\frac {\sin(\pi *d*\sin(\theta )/\lambda )^{2}*\lambda ^{2}}{(\pi ^{2}*d^{2}*\sin(\theta )^{2})}}}

I 是干涉因子：

I=sin⁡ ⁡ -->(π π -->∗ ∗ -->a∗ ∗ -->sin⁡ ⁡ -->(θ θ -->)∗ ∗ -->N/λ λ -->)2(N2∗ ∗ -->sin⁡ ⁡ -->(π π -->∗ ∗ -->a∗ ∗ -->sin⁡ ⁡ -->(θ θ -->)/λ λ -->)2){\displaystyle I={\frac {\sin(\pi *a*\sin(\theta )*N/\lambda )^{2}}{(N^{2}*\sin(\pi *a*\sin(\theta )/\lambda )^{2})}}}

资料来源

www.celomc.com

Adapted from a public domain entry in Federal Standard 1037C

National Optical Astronomy Observatories entry regarding volume phase holography gratings

Hutley, Michael, Diffraction Gratings (Techniques of Physics), Academic Press (1982)[1]

Loewen, Erwin & Evgeny Popov, Diffraction Gratings and Applications, CRC; 1 edition (1997)[2]

Palmer, Christopher, Diffraction Grating Handbook, 6th edition, Newport Corporation (2005)[3]

Greenslade, Thomas B., "Wire Diffraction Gratings," The Physics Teacher, February 2004. Volume 42 Issue 2, pp. 76-77[4]

Abrahams, Peter, Early Instruments of Astronomical Spectroscopy[5]

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。