使用在图像初步创建（通常使用网格骨架构建，建模（3Dmodeling））之后，就要进行渲染了。渲染将会在上面添加位图纹理或者程序纹理、照明、凸凹纹理映射以及相对于其它物体的位置。得到的结果就是消费者或者观察者所能看到的完整图像。对于电影动画来说，需要渲染几幅或几帧图像，并且将这些图像在动画制作程序中将它们连结在一起。大多数的三维图像编辑程序都能够完成这项工作。特性渲染的图像有许多显著的特性，渲染研究的领域，也主要集中在寻找：高效模拟这些特性的方法。有些特性只与特定的算法有关，有些却与多个算法相关。浓淡处理—表面颜色与亮度随光照的变化纹理映射—在表面生成细节的方法凸凹纹理映射—在表面模拟小凸凹的方法距离模糊—光照穿过不清澈的大气时的模糊阴影—阻挡光照的效果柔和阴影—模拟光的衍射下的阴影反射—镜子或者非常光滑的反射透明—固体明显允许光线穿过半透明—光线通过固体高度散射折射—与透明相关的光线弯曲...

Reyes架构的设计目标Reyes架构的设计遵从以下目标：模型复杂性和多样性：为了产生复杂和样式丰富的图像，渲染系统的用户必须能通过分形或粒子系统等，经由编写程序生成大量复杂的几何结构。复杂着色：场景的复杂度通常由光线和物体表面的相互作用产生。通常，在计算机图形学里，这是通过使用纹理来表现的，纹理可以是一组像素，用于描述表面位移（置换）、透明度或反射率等。Reyes允许用户用计算机程序来描述表面结构和光学互作用，而不是简单的数据查询表，并和可编程着色器结合。算法的一个重要目标是减少处理器从存储器中读取纹理的时间。避免光线追踪：Reyes架构提出的时候，计算机的处理能力和存储量都很有限，意味着使用光线追踪需要耗费几万小时才能渲染完一个图像，Reyes算法避免使用光线追踪，因此渲染快的多，并且图像也非常逼真。速度：（单个计算机）一年能渲染完成一部每秒24帧的两小时影片，即平均每帧只需要渲染3分...

历史扫描线渲染技术的首次公开发表是1967年Wylie、Romney、Evans以及Erdahl完成的。其它一些扫描线渲染的方法分别是由Bouknight于1969年以及Newell、Newell与Sancha于1972年开发的。许多这方面的早期研究工作都是由犹他大学的IvanSutherland图形研究组以及位于犹他州盐湖城的Evans&Sutherland公司完成的。参见扫描线像素Rasterscan

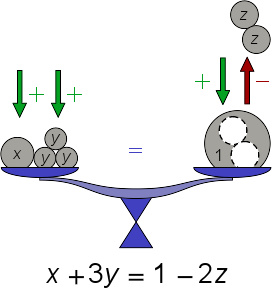
“方程”一词的来历方程一词出现在中国早期的数学专著《九章算术》中，其“卷第八”即名“方程”。卷第八（一）为：翻成白话即为：现在这里有上等黍3捆、中等黍2捆、下等黍1捆，打出的黍共有39斗；有上等黍2捆、中等黍3捆、下等黍1捆，打出的黍共有34斗；有上等黍1捆、中等黍2捆、下等黍3捆，打出的黍共有26斗。问1捆上等黍、1捆中等黍、1捆下等黍各能打出多少斗黍？其“方程术”用阿拉伯数字表示即为：123232311263439{\displaystyle{\begin{array}{*{20}c}1&2&3\\2&3&2\\3&1&1\\{26}&{34}&{39}\\\end{array}}}《九章算术》采用直除法即以一行首项系数乘另一行再对减消元来解方程。若设可打出黍的斗数分别为1捆上等黍x{\displaystylex\,}斗、1捆中等黍y{\displaystyley\,}斗、1捆下等黍z...

公式齐奥尔科夫斯基火箭方程的核心内容是：基于动量守恒原理，任何一个装置，通过一个消耗自身质量的反方向推进系统，可以在原有运行速度上，产生并获得加速度。其认为，任何一次飞行器轨道变化（速度变化）或者多次轨道变化都遵循如下公式:ΔΔ-->v=veln⁡⁡-->m0m1{\displaystyle\Deltav\=v_{e}\ln{\frac{m_{0}}{m_{1}}}}其还可以写成如下方式：m1=m0e−−-->ΔΔ-->v/ve{\displaystylem_{1}=m_{0}e^{-\Deltav\/v_{e}}}或者m0=m1eΔΔ-->v/ve{\displaystylem_{0}=m_{1}e^{\Deltav\/v_{e}}}或者1−−-->m1m0=1−−-->e−−-->ΔΔ-->v/ve{\displaystyle1-{\frac{m_{1}}{m_{0}}}=1-e^{-...