词源学

英文术语“lepton”源自希腊语“ λεπτόν ”（ leptón ），是“ λεπτός ”（ leptós ）的中性，含意为"小、薄"。 里昂·洛森斐（Léon Rosenfeld）于1948年最先为英文术语“lepton”命名。

这命名不正确地假定所有轻子的质量都很小。在洛森斐命名那时，学术界只知道有电子与μ子两种轻子。它们的质量的确很小，电子的质量为 0.511MeV ， μ子的质量为 105.7 MeV ， 比质子的质量 938.3 MeV 轻很多 。可是，在1970年代中期发现的τ子，它的质量是 1,777 MeV ，几乎是质子的两倍。

历史

马丁·佩尔与他的实验团队发现τ子。

最先被辨识的轻子是电子，英国物理学者约瑟夫·汤姆孙与实验团队于1897年发现电子。 1930年，沃尔夫冈·泡利大胆假设电中微子存在，这是为了解释β衰变的能量缺失问题，挽救能量守恒定律；泡利认为，所有最初与最终观察到的粒子的能量差，都被一种尚未探测到的粒子带走了，这粒子具有电中性，不会留下轨迹，所以很难探测到。 三年后，恩里科·费米给出理论，成功描述β衰变，强力支持泡利的假设。费米将这粒子命名为“中微子”，意思为“微小的中子”。在那时期，电中微子被称为中微子，因为尚未发现其它世代的中微子。1956年，克莱德·科温与弗雷德里克·莱因斯共同完成 科温-莱因斯中微子实验 （ 英语 ： Cowan–Reines neutrino experiment ） 首先直接观察到中微子的存在。

在电子被发现大约40年之后，卡尔·安德森于1936年发现了μ子。由于它的质量，μ子最初被归类为介子，而不是轻子。 渐渐地，学者发觉μ子的性质更接近电子，只是质量比较大，而且μ子不会感受到强相对作用，不具有介子的性质。1947年，才有学者开始提议一群粒子被归类为轻子的概念。 后来，μ子被重新归类，μ子、电子与电中微子一起被归类为轻子。1962年利昂·莱德曼、梅尔文·施瓦茨与杰克·施泰因贝格尔做实验直接探测到μ中微子，证实不只一种中微子存在。

马丁·佩尔与他的实验团队于1975年完成实验首先探测到τ子。 如同电子与μ子，物理学者认为它应该也有伴随的中微子，这是因为他们观察到类似β衰变的缺失能量问题。费米实验室的直接观察τ中微子实验（Direct Observation of the NU Tau，DONUT ）团队于2000年探测到τ中微子参与作用的证据。

虽然现有数据符合三个世代的轻子，有些粒子物理学者仍在寻找第四代带电轻子。这种带电轻子的质量下限为 100.8GeV ， 伴随它的中微子最少应该带有质量 45.0GeV 。

性质

自旋与手征性

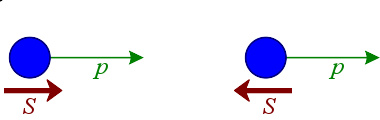
右手螺旋性（ P {\displaystyle \mathbf {P} } 、 S {\displaystyle \mathbf {S} } 同向）与左手螺旋性（ P {\displaystyle \mathbf {P} } 、 S {\displaystyle \mathbf {S} } 反向）。

轻子是自旋 ⁄ 2 粒子，只能处于两种自旋态：上旋或下旋。自旋统计定理将它们按照自旋归类为费米子，遵守泡利不相容原理，因此任何两个全同的轻子不能同时占有相同的量子态。

手征性与螺旋性（helicity）是与自旋紧密相关的两种性质，螺旋性跟粒子的自旋与动量之间的相对方向有关；假若是同向，则粒子具有右手螺旋性，否则粒子具有左手螺旋性。对于不带质量粒子，这相对方向与参考系无关，可是，对于带质量粒子，由于可以借着洛伦兹变换来改换参考系，从不同的参考系观察，粒子动量不同，因此翻改螺旋性，可以从右手螺旋性翻改为左手螺旋性，或从左手螺旋性翻改为右手螺旋性。手征性是通过庞加莱群（Poincaré group）的变换来定义的性质。对于不带质量粒子，手征性与螺旋性一致；对于带质量粒子，手征性与螺旋性有别。

在很多量子场论里，例如量子电动力学与量子色动力学，并没有对左手与右手费米子作任何区分，可是，在标准模型的弱相互作用理论里，按照手征性区分的左手与右手费米子被非对称地处理，只有左手费米子参与弱相互作用，右手中微子不存在。这是宇称违反的典型例子。

电磁相互作用

轻子-光子相互作用。

轻子的电荷 Q {\displaystyle Q} 决定了它所产生的电磁场，也决定了它怎样响应外电磁场。轻子的每个世代的组员都有一个带电轻子 Q = − − --> 1 {\displaystyle Q=-1} 与一个中性轻子 Q = 0 {\displaystyle Q=0} ，例如，第一代轻子为电子 e − 与电中微子 ν e 。

使用量子场论的语言，带电轻子所涉及的电磁相互作用表达为这轻子与电磁场的量子（光子）彼此之间的相互作用。右图是电子-光子相互作用的费曼图。

由于轻子具有自旋，带电轻子会产生磁场，磁偶极矩 μ μ --> {\displaystyle \mu } 为

其中， m {\displaystyle m} 是轻子的质量， g {\displaystyle g} 是轻子的g-因数（g-factor）。

一阶近似量子力学预测，对于所有轻子，g-因数为2；可是高阶量子效应，因为费曼图里的虚粒子圈对于这数字给出修正。这些修正，称为反常磁偶极矩（anomalous magnetic dipole moment），对于量子场论模型的细节非常敏感，因此是准确检验标准模型的好机会。对于电子测量其反常磁偶极矩所得到的实验数值符合理论结果至8个有效数字。

弱相互作用

在标准模型里，轻子可以按照手征性分为左手轻子与右手轻子；左手轻子的弱同位旋T为 ⁄ 2 ，左手带电轻子与左手中微子的弱同位旋投影（弱同位旋的第三分量）T 3 分别为- ⁄ 2 、+ ⁄ 2 ，弱相互作用是由它们组成二重态（doublet state） ( ν e L , e − L ) 共同实现；右手带电轻子的弱同位旋T为0，形成单态，不参与弱相互作用；右手中微子并不存在。

希格斯机制将弱同位旋SU(2)与弱超荷U(1)对称的四个规范场，重新组合成传递弱相对作用的三个带质量玻色子 （ W + 、 W − 、 Z 0 ）与传递电磁相对作用的不带质量玻色子（光子）。通过盖尔曼-西岛方程，可以从弱同位旋投影 T 3 与弱超荷 Y W 计算出电荷 Q ：

为了符合观察到的任何粒子所带有的电荷，所有左手弱同位旋二重态 ( ν e L , e − L ) 的弱超荷 Y W 必须为-1，而右手弱同位旋单态 ( e − R ) }的弱超荷 Y W 必须为-2。

质量

在标准模型里，每一个轻子原本不具有内秉质量；通过与希格斯场耦合，带电轻子获得有效质量，但中微子仍旧不带质量，这意味着不同世代的带电轻子不会相互混合，与夸克的物理行为大不相同。这结果符合当今实验数据。

但是，从实验中得知（最显著的是中微子振荡实验）， 中微子实际带有微小质量，大约小于 2eV 。 这意味着后标准模型（beyond the Standard Model）的物理现象。当今最被物理学者青睐的理论延伸是翘翘板机制，它可以解释为什么左手中微子的质量远轻于对应的带电轻子，为什么做实验尚未能观察到任何右手中微子。

轻子数

每一代轻子的成员组成一个弱同位旋二重态：

每一代弱同位旋二重态的成员都被分派一个轻子数。在标准模型里，轻子数守恒。 电子与电中微子的电子数L e 为1。μ子与μ中微子的μ子数L μ 为1。τ子与τ中微子的τ子数L τ 为1。 反轻子的轻子数为对应轻子的轻子数乘以−1。

轻子数守恒的意思就是同类氢子数的代数和保持不变，当粒子耦合时；这意味着只有同一代的轻子与反轻子才能成对产生。例如，以下过程是被允许的：

以下过程是不被允许的：

但是，中微子振荡违反单独轻子数守恒，这是后标准模型物理的确凿证据。更强的守恒定律是总轻子数守恒。中微子振荡遵守总轻子数守恒。但是， 手征反常 （ 英语 ： chiral anomaly ） 稍微违反了这守恒定律。

普适性

轻子与对应的中微子之间的相互作用与风味无关，换句话说，对于电子与电中微子之间的相互作用、μ子与μ中微子之间的相互作用、τ子与τ中微子之间的相互作用，假若将质量差别纳入考量，则这三种相互作用的效应相等。这性质称为轻子相互作用的“普适性”。所有已知实验数据与这种普适性一致 做实验测量τ子与μ子的平均寿命，或Z玻色子衰变为轻子的部分衰变宽度，可以检验这性质。在大型正负电子对撞机与史丹福直线加速器里，完成了很多这类检验普适性的实验。

对于过程μ −→e −+ν e+ν μ，μ子的衰变率 Γ Γ --> {\displaystyle \Gamma } 以方程表示为（更详尽内容，请参阅μ子衰变）

其中， K 1 {\displaystyle K_{1}} 是常数， G F {\displaystyle G_{F}} 是费米耦合常数， m μ μ --> {\displaystyle m_{\mu }} 是μ子的质量。

对于过程τ −→e −+ν e+ν τ，τ子的衰变率 Γ Γ --> {\displaystyle \Gamma } 以同样形式的方程表示为

其中， K 2 {\displaystyle K_{2}} 是常数， m τ τ --> {\displaystyle m_{\tau }} 是τ子的质量。

μ子-τ子普适性意味着 K 1 = K 2 {\displaystyle K_{1}=K_{2}} 。普适性也能够解释μ子寿命与τ子寿命之间的关系。轻子的寿命 L l {\displaystyle L_{l}} 与衰变率 Γ Γ --> {\displaystyle \Gamma } 之间的关系为

其中， B ( x → → --> y ) {\displaystyle B(x\rightarrow y)} 与 Γ Γ --> ( x → → --> y ) {\displaystyle \Gamma (x\rightarrow y)} 分别标记过程 x → → --> y {\displaystyle x\rightarr共振 y} 的分支比与共振宽度。

τ子与μ子的寿命比因此为

从实验获得的μ子分支比与τ子分支比，可以计算出寿命比为大约 1.328 × 10 ，实验测量得到的寿命比为 ~ 1.323 × 10 。两者之差异是因为 K 1 {\displaystyle K_{1}} 、 K 2 {\displaystyle K_{2}} 实际并不是常数，它们与轻子的质量有关。

另外，由于电子-μ子普适性，τ子衰变为电子的分支比(17.85%) 与衰变为μ子的分支比 (17.36%) 相同（在误差范围内）：

轻子列表

参阅

粒子列表

夸克

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。