汤姆孙散射的描述

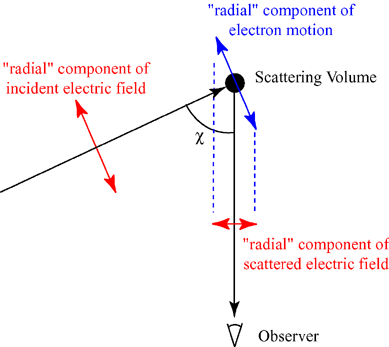
在汤姆孙散射中，入射波和观察到的散射波电场都可以分解为位于观察平面（由入射波传播方向和散射波传播方向构成的平面）内和垂直于观察平面的分量。习惯上，那些位于平面内的分量被称作“径向”，而垂直于平面的分量被称作“切向”，这都是对于观察者而言的。

右图所示的是散射在观察平面内的情形，图中显示了入射电场的径向分量是造成位于散射点的带电粒子在该方向上发生运动的原因，并且这一运动也位于观察平面内。此外还可以看出散射波的振幅正比于入射波与散射波夹角χ的余弦，而散射波的光强正比于振幅的平方，从而含有cos(χ)这一因子。而垂直于观察平面的切向分量则不会产生类似的影响。

描述散射的最佳方法是引入一个发射系数ϵ ϵ -->{\displaystyle \epsilon \,}，而ϵ ϵ -->dtdVdΩ Ω -->dλ λ -->{\displaystyle \epsilon {\rm {{d}t{\rm {{d}V{\rm {{d}\Omega {\rm {{d}\lambda \,}}}}}}}}}是在时间间隔dt内被体元dV{\displaystyle {\rm {立体角V\,}}}散射至立体角dΩ Ω -->{\displaystyle {\rm {{d}\Omega \,}}}这一方向内，且波长介于λ λ -->{\displaystyle \lambda \,}和λ λ -->+dλ λ -->{\displaystyle \lambda +{\rm {{d}\lambda \,}}}之间的入射波能量。从观察者的角度而言，汤姆孙散射存在有两个发射系数，一个是对应着径向偏振波的发射系数ϵ ϵ -->r{\displaystyle \epsilon _{r}\,}，另一个是对应着切向偏振波的发射系数ϵ ϵ -->t{\displaystyle \epsilon _{t}\,}。它们分别由下面关系给出：

其中n是位于散射点的带电粒子密度，I是入射波的通量（单位时间单位波长范围内辐射到单位面积的能量）。而σ是带电粒子的汤姆孙散射的微分截面（面积/立体角），其表达式为

其中第一个表达式的单位制是厘米-克-秒制，第二个表达式的单位制是国际单位制；q是单个粒子所带电量，m是单个粒子所带质量，ϵ ϵ -->0{\displaystyle \epsilon _{0}}是真空介电常数。

注意到这正是一个具有质量m和电荷q的点粒子的经典半径。对于电子而言，散射微分截面为

这里λ λ -->e{\displaystyle \lambda _{e}}是电子的康普顿波长。

散射波辐射出的总能量可通过对发射系数求和并对空间中所有方向积分给出：

这里σT是总散射截面。

对于电子而言，这个散射截面为

汤姆孙散射的实例

在宇宙诞生的最初几天里，宇宙中产生的光子不断地被自由电子散射，从而导致了早期宇宙的不透明性，这一散射过程即为汤姆孙散射。而宇宙微波背景辐射正是这一散射最终演化的产物，威尔金森微波各向异性探测器和普朗克卫星正在试图对它的线偏振性进行观测。

太阳辐射出的光子被日冕中的自由电子散射，从而形成了K冕，这一散射过程也是汤姆孙散射。美国国家航空航天局发射的日地关系天文台通过采用两个独立卫星对K冕进行测量，从而可以得到太阳周围自由电子密度的三维图像。

逆康普顿散射也可以看作是相对论性粒子自身参考系下的汤姆孙散射。

参见

康普顿散射，体现光的粒子性的光子－电子散射。

克莱因－仁科公式，基于量子电动力学的光子－电子散射的微分截面计算公式。

参考文献

Jackson, John D. Classical Electrodynamics 3rd. New York: Wiley. 1998. ISBN 0-471-30932-X. 

Billings, Donald E., ``A Guide to the Solar Corona, Academic Press, New York 1966.

汤姆孙散射的课程笔记之二

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。