物理量及定律

原表达形式

其中：

定理假设

使用伯努利定律必须符合以下假设，方可使用；如没完全符合以下假设，所求的解也是近似值。

定常流动（或称稳定流，Steady flow）：在流动系统中，流体在任何一点之性质不随时间改变。

不可压缩流（Incompressible flow）：密度为常数，在流体为气体适用于马赫数 M {\displaystyle M} 小于0.3的情况。

无摩擦流（Frictionsless flow）：摩擦效应可忽略，忽略黏滞性效应。

流体沿着流线流动（Flow along a streamline）：流体元素（element）沿着流线而流动，流线间彼此是不相交的。

推论过程

考虑一符合上述假设的流体，如图所示：

流体因受压力的推动而得之能量：

流体因引力做功所损失的能量：

流体所得的动能可以改写为：

根据能量守恒定律，流体因受力所得的能量＋流体因引力做功所损失的能量＝流体所得的动能。

由连续方程可知：

令 constant = Δ Δ --> V {\displaystyle {\mbox{constant}}=\Delta V\;}

从等式两边除以 Δ Δ --> t {\displaystyle \Delta t\;} 及 Δ Δ --> V {\displaystyle \Delta V\;} 可得：

或

特例：托里切利定律

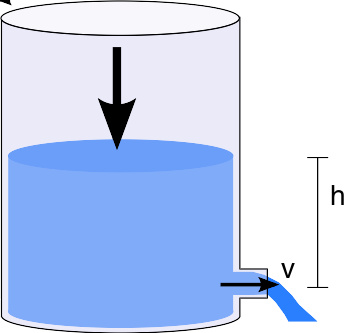
当液体因受到地心吸力的作用而流出时，其速度等于 2 g h {\displaystyle {\sqrt {2gh}}} ，其中 g {\displaystyle g} 为引力的加速度， h {\displaystyle h} 为开口的中心和液体最高面的距离。这个速度刚好等于液体从离地 h {\displaystyle h} 的地方以自由落体的方式下落时，着地前的速度（但实际上因为有空气阻力，所以实际情形一般不会以自由落体的方式下落）。

伯努利定律演示实验

简易喷枪

运作中的简易喷枪

简易喷雾器，以大吸管固定两只小吸管使之夹角略小于直角，因从吸管吹出之气体流速较快，压力较一大气压力为低，因此能够将水经由下端吸管中吸起，并于开口处加速破碎成雾滴，模型制作用喷枪以及工业用喷漆喷枪多为此种设计。

不过因为伯努利定律是假设流体沿着流线流动，探讨同一流线上二点的速度及压力变化。因此有些现象和伯努利定律无关，例如悬浮保丽龙球，将可折弯的吸管一端向上稳定吹出气体，将一直径约3公分之保丽龙球放置于气柱上，保丽龙球能够悬浮晃动于一定区域中，因为保丽龙球上方和下方的气流不是同一流线，这和伯努利定律无关，是康达效应的结果 。

可压缩流体的伯努利定律

伯努利从观察液体的行为中推导出伯努利方程，但他的方程是只能应用在不可压缩的流体，以及虽然可压缩但流速非常慢的流体（也许可以到1/3的声速）。利用基本物理原理，可以发展出类似的方程，以适用于可压缩的流体。以下有几个类似于伯努力定律，能应用在不同领域方程。它们的推导只运用了像是牛顿第二定律和热力学第一定律的基本物理定律。

可压缩流体之流体力学

对于可压缩的流体，在保守力的作用之下，所得到的守恒式为

其中:

在工程领域，在海拔比较高的地方，其压力会比地表来的小，而且流体流动的时间通常是相当的小，如同绝热系统般。在这种情形下，上述的方程即

其中：

在可压缩流体可以应用的地方，因为高度变化与其他变因相比小的很多，故gz项可以省略，所以较常用的方程为

其中:

可压缩流动的热力学

另一个适合使用在热力学的公式是

其中：

请注意 w = ϵ ϵ --> + p ρ ρ --> {\displaystyle w=\epsilon +{\frac {p}{\rho }}} ，其中 ϵ ϵ --> {\displaystyle \epsilon } 为热力学单位质量的能量，即比内能（specific internal energy）； p {\displaystyle p} 为压力； ρ ρ --> {\displaystyle \rho } 为密度。

公式右侧的常数通常被称为伯努力常数，常被写为 b {\displaystyle b} 。当在绝热非黏滞性的流动，没有能量的流进或流出时， b {\displaystyle b} 在任何曲线都是常数。

当 Ψ Ψ --> {\displaystyle \Psi } 变化可以忽略，一个非常有用的形式的方程是:

其中 w 0 {\displaystyle w_{0}} 是焓的总量。

延伸阅读

Ting, J.fluid mechanics. createspace. 2014. ISBN 978-149426094-1.

Batchelor, G.K.An Introduction to Fluid Dynamics. Cambridge University Press. 1967. ISBN 0-521-66396-2.

Clancy, L.J. Aerodynamics. Pitman Publishing, London. 1975. ISBN 0-273-01120-0.

Lamb, H.Hydrodynamics 6th. Cambridge University Press. 1993. ISBN 978-0-521-45868-9. Originally published in 1879; the 6th extended edition appeared first in 1932.

Landau, L.D.;Lifshitz, E.M.Fluid Mechanics.Course of Theoretical Physics2nd. Pergamon Press. 1987. ISBN 0-7506-2767-0.

Chanson, H.Applied Hydrodynamics: An Introduction to Ideal and Real Fluid Flows. CRC Press, Taylor & Francis Group. 2009. ISBN 978-0-415-49271-3.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。