历史

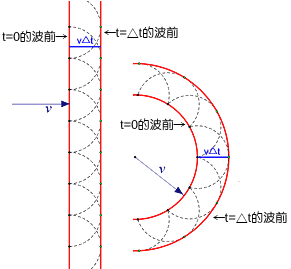
按照惠更斯原理，波的直线传播与球面传播。

1678年，惠更斯完成著作《光论》（《Traitė de la Lumiere》）。1690年这本书公开发行。在这本书中他提出“惠更斯原理”：

借着这原理，他可以给出波的直线传播与球面传播的定性解释，并且推导出反射定律与折射定律；但是他并不能解释，为什么当光波遇到边缘、孔径或狭缝时，会偏离了直线传播，即衍射效应。惠更斯假定次波只会朝前面方向传播，而不会朝后面方向传播。他并没有解释为什么会发生这种物理行为。 惠更斯原理是一种光波动说。这假说是根据1664年罗伯特·胡克的提议。胡克本人牛顿的光微粒说。两位大师争吵不休，直至胡克往生。在那时期，由于艾萨克·牛顿在其它物理领域的成功，他被公认是光本质争论的赢家。

菲涅耳在惠更斯原理的基础上假设这些次波会彼此发生干涉，因此惠更斯－菲涅耳原理是惠更斯原理与干涉原理的结晶。 用这种观点来描述波的传播，可以解释波的衍射现象。特别地，惠更斯－菲涅耳原理是建立衍射理论的基础，并指出了衍射的实质是所有次波彼此相互干涉的结果。为了符合实验结果，他又添加了一些关于次波的相位与波幅的假定。这些假定引导出的预测与许多实验观察相符合，包括泊松光斑，也对于为什么波只会朝前面方向传播，而不会朝后面方向传播这问题给出一个定量的解释。

1818年，菲涅耳将他的论文提交给法兰西学术院的评委会。评委会的会员西莫恩·泊松阅读完毕后认为，假若菲涅耳的理论成立，则将光波照射于一小块圆形挡板，其形成的阴影的中央必会有一个亮斑，因此，他推断这理论不正确。但是，评委会的另一位会员，弗朗索瓦·阿拉戈亲自动手做这实验，获得的结果与预测相符合，证实菲涅耳原理正确无误。真正最先观察到这现象的是法国-意大利天文学者吉雅科莫·马劳地（Giacomo Maraldi），但他于1723年获得的研究结果在那时代并没有得到重视。 这实验是支持光波动说的强有力的证据。这实验与托马斯·杨的双缝实验共同反驳了艾萨克·牛顿主导的光微粒说。

数学表述

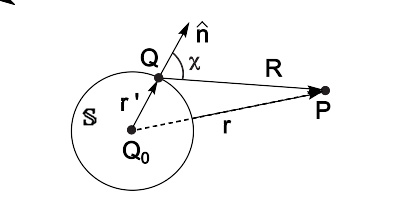
从点波源Q 0 发射出的球面波，其波前的任意一点Q可以视为次波的波源，这些次波会各自在点P贡献出波扰叠加在一起，因此形成总波扰。

如右图所示，假设点波源Q 0 发射出的球面波，其复值波幅为 ψ ψ --> 0 {\displaystyle \psi _{0}} 、波长为 λ λ --> {\displaystyle \lambda } 、波数为 k = 2 π π --> / λ λ --> {\displaystyle k=2\pi /\lambda } 。对于球面波，波扰的数值大小与距离 r ′ {\displaystyle r"} 成反比，相位随着波数 k {\displaystyle k} 与距离 r ′ {\displaystyle r"} 的乘积而改变。因此，在与点波源Q 0 相离距离为 r ′ {\displaystyle r"} 的点Q，其波扰为

应用惠根斯原理与波的叠加原理，将所有与点Q同波前的点波源，其所发射出的次波对于点P的贡献叠加在一起，可以得到在点P的总波扰。为了与做实验获得的结果相符合，菲涅耳还发觉必须将计算结果乘以常数因子 − − --> i / λ λ --> {\displaystyle -i/\lambda } 与“倾斜因子” K ( χ χ --> ) {\displaystyle K(\chi )} ；其中， χ χ --> {\displaystyle \chi } 是三角形Q 0 PQ在点Q的外角。

第一个修正意谓著次波与主波的相位差为 π π --> / 2 {\displaystyle \pi /2} ，相对于主波，次波的相位超前 π π --> / 2 {\displaystyle \pi /2} ，另外，次波与主波之间的波幅比率为 1 : λ λ --> {\displaystyle 1:\lambda } 。

对于第二个修正，菲涅耳假定，当 χ χ --> = 0 {\displaystyle \chi =0} 时，倾斜因子 K ( χ χ --> ) {\displaystyle K(\chi )} 是最大值；而当 π π --> ≤ ≤ --> χ χ --> ≤ ≤ --> π π --> / 2 {\displaystyle \pi \leq \chi \leq \pi /2} 时，倾斜因子 K ( χ χ --> ) {\displaystyle K(\chi )} 等于零。

假若不做这假定，则次波会朝着所有可能方向传播，这包括了向前传播与向后传播；但是，做实验并没有观察到向后传播的波，为了符合这实验结果，必须假定次波朝着各个方向传播的波幅不一样，对于前方传播的波幅很大，对于后方传播的波幅很微小，甚至等于零。倾斜因子的主要功能就是调整次波朝着各个方向传播的波幅。

经过修正后，从点波源Q 0 发射出的波，其波前的微小面元素 d S {\displaystyle \mathrm {d} S} 部分，对于点P贡献出的微小复值波扰 d ψ ψ --> ( r ) {\displaystyle \mathrm {d} \psi (\mathbf {r} )} 为

其中， R {\displaystyle R} 是点Q与点P之间的距离。

在点P的复值波扰为

其中， S {\displaystyle \mathbb {S} } 是积分曲面。

从基尔霍夫衍射公式，可以推导出惠更斯－菲涅耳原理。菲涅耳在惠更斯－菲涅耳原理里凭空提出的假定与修正，在这推导过程中，会自然而然地显露出来。 惠更斯－菲涅耳方程可以视为基尔霍夫衍射公式的一个近似。古斯塔夫·基尔霍夫给出了倾斜因子 K ( χ χ --> ) {\displaystyle K(\chi )} 的表达式：

注意到根据这表达式，当 χ χ --> = 0 {\displaystyle \chi =0} 时，倾斜因子 K ( χ χ --> ) {\displaystyle K(\chi )} 是最大值；而当 χ χ --> = π π --> / 2 {\displaystyle \chi =\pi /2} 时，倾斜因子 K ( χ χ --> ) {\displaystyle K(\chi )} 不等于零。

量子电动力学

惠更斯原理可以视为空间的各向同性的后果。“空间的各向同性”指的是，在空间里，对于所有方向，物理性质都一样。在各向同性空间（或各向同性介质）里足够微小的区域内产生的任何波扰，必会从那区域以径向传播。由这波扰产生的波动，又会在其它区域形成波扰，如此这般继续不断。所有波动的叠加形成了观察到的波动传播图样。

量子电动力学的关键基础之一是空间的各向同性。在这空间里，任意物体的波函数会沿着所有未被阻碍的可能路径传播。当对于所有可能路径做积分计算时，若将波函数的相位因子正比于路径距离这因素纳入考量，则波函数与波函数彼此之间的相互干涉会正确地预测出实验观察到的各种现象。

单缝衍射

图的右半部分为观察屏水平方向上的辐照度分布，辐照度曲线在 θ θ --> {\displaystyle \theta } -轴的第一个零点 θ θ --> m i n , 1 {\displaystyle \theta _{min,1}} 被称为“第一极小值”；图的左半部分为单缝衍射的示意图，狭缝处诸点光源发出的光波以角度 θ θ --> {\displaystyle \theta } 传播到达第一极小值。这里，我们认为这些光束与狭缝垂直平分线的夹角均为 θ θ --> {\displaystyle \theta } ，是基于 L {\displaystyle L} 远大于 d {\displaystyle d} 的前提。

惠更斯－菲涅耳原理最常见的应用之一，是计算平面波（通常为可见光、无线电波、X射线或电子等）照射到具有任意形状孔径的挡板的衍射行为。根据原理所述，位于孔径的每一点都是都是点波源，能够发射出向各个方向传播的球面子波。将所有从这些点波源发射出的球面波通过干涉原理进行叠加，平面波通过孔径后的在任意时刻的波前。

考虑最简单的单缝衍射情形，例如在计算出现于观察屏的衍射图样时，先将这条相对较宽的单缝分成无数更窄的狭缝，然后将它们看作是新的点波源并计算彼此的干涉。如果将单缝分成两个小狭缝，当它们的子波的光程差对应着 λ λ --> / 2 {\displaystyle \lambda /2} 时有相消干涉；如果分成三个小狭缝，则这一光程差对应 λ λ --> / 3 {\displaystyle \lambda /3} 时有相消干涉；以此类推到无数个小狭缝的情形，则位于两端的小狭缝的光程差需要恰好为 λ λ --> {\displaystyle \lambda } 时才会得到完全的相消干涉。以方程表达，假设单缝的宽度为 d {\displaystyle d} ，“第一极小值”的位置与中央轴的夹角为 θ θ --> {\displaystyle \theta } 则

一般孔径的衍射

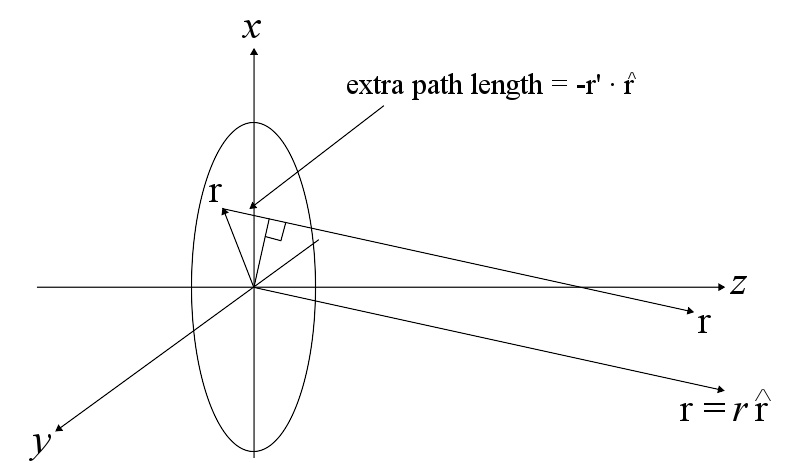
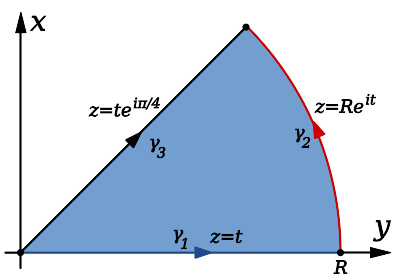
一般孔径衍射数学推导示意图。

上面讨论单缝衍射时所用的定性分析难以推广到一般形状孔径的衍射中。而基尔霍夫在惠更斯－菲涅耳原理的基础上将其数学化，认为这个原理可以用一个近似积分来表示。从一个点波源发射出的进行波在位置 r {\displaystyle \mathbf {r} } 上的振幅 ψ ψ --> {\displaystyle \psi } 可由频域下对应的波方程（亥姆霍兹方程）的解给出：

其中， δ δ --> ( r ) {\displaystyle \delta ({\mathbf {r}})} 狄拉克狄拉克δ函数。

由于在这里狄拉克δ函数仅是径向 r {\displaystyle {\mathbf {r}}} 的函数，则在球坐标系下可以将拉普拉斯算符分解为

直接代入波方程，得到的方程的解是标量的格林函数，并在球坐标系下可表为

这个解的形式是假设了描述波源的狄拉克函数位于原点。对于任意位置 r ′ ′ --> {\displaystyle {\mathbf {r}}^{\prime }} 的源点，在场点 r {\displaystyle {\mathbf {r}}} 的标量格林函数可表为

由此，对于入射到孔径上的电场 E i n c ( x , y ) {\displaystyle E_{\rm {inc}}(x,y)} ，从这一孔径发出的电场由入射场和格林函数对孔径几何分布的面积分给出：

其中孔径上的点源坐标由下式给出：

在远场极限下，光线可认为彼此平行，此时格林函数

可简化为

则在远场区（夫琅禾费区），场的表达式为

并由于

以及

从而，从一个平面孔径发出的电场在夫琅禾费区的表达式为

令

和

则一个平面孔径的夫琅禾费衍射具有傅里叶变换的形式：

这表明在衍射的远场区，电场的形式由孔径的几何分布在空间上的傅里叶变换给出。也就是说当惠更斯－菲涅耳原理应用于孔径时，它表明夫琅禾费衍射的图样是孔径形状在空间上的傅里叶变换。这一原理用另一种语言——傅里叶光学——也可以做出等价的描述。

参见

格林函数

格林定理

格林恒等式

基尔霍夫积分定理

双缝实验

费马原理

菲涅尔衍射

傅里叶光学

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。