人物生平

出生于普鲁士公国首都哥尼斯堡，是勃兰登堡- 普鲁士的一部分，哥德巴赫是牧师的儿子。他曾就读于皇家阿尔伯特大学。完成学业后，他从1710年到1724年通过欧洲长途教育航行，访问其他德国各州，英国，荷兰，意大利和法国，与许多着名的数学家会面，如莱布尼兹，莱昂哈德·欧拉和尼古拉斯一伯努利。回到哥尼斯堡，他结识了格奥尔·伯恩哈德和雅各布·赫尔曼。

他于1725 年继续在新开设的圣彼得堡科学院工作，担任数学教授和该学院的历史学家。 1728年，彼得二世成为俄罗斯沙皇时，哥德巴赫成为他的导师。 1742年，他进入俄罗斯外交部。

 哥德巴赫擅长多个语种 - 他用德语和拉丁语写日记，他的信件用德语，拉丁语，法语和意大利语写成，而官方文件则使用俄语，德语和拉丁语。

他于1764年11月20日在莫斯科逝世，享年74岁 。

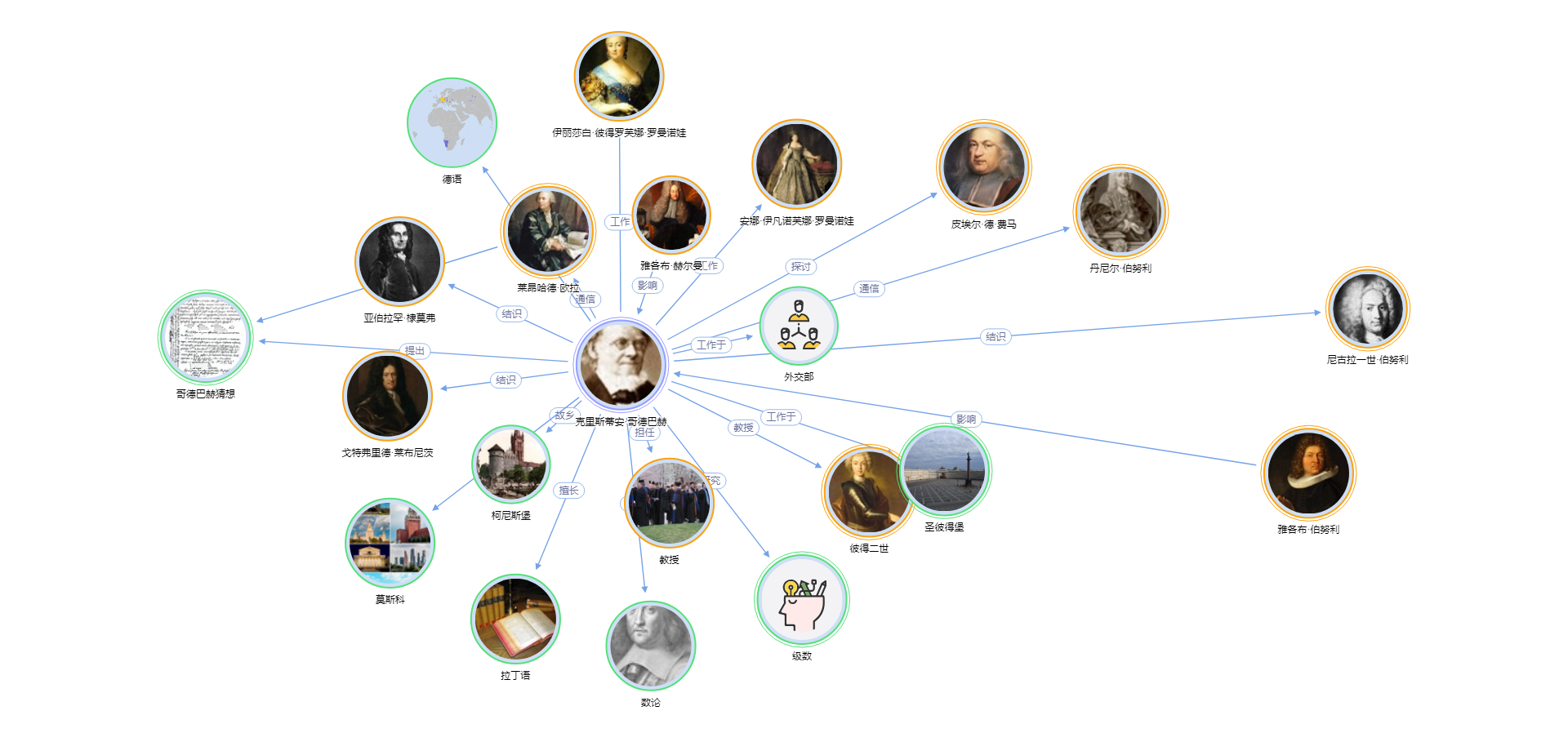
查看详细关系图哥德巴赫

哥德巴赫猜想

哥德巴赫猜想（Goldbach"s conjecture）是数论中存在最久的未解问题之一。这个猜想最早出现在1742年普鲁士人克里斯蒂安·哥德巴赫与瑞士数学家莱昂哈德·欧拉的通信中。用现代的数学语言，哥德巴赫猜想可以陈述为：

“任一大于2的偶数，都可表示成两个素数之和。”

这个猜想与当时欧洲数论学家讨论的整数分拆问题有一定联系。整数分拆问题是一类讨论“是否能将整数分拆为某些拥有特定性质的数的和”的问题，比如能否将所有整数都分拆为若干个完全平方数之和，或者若干个完全立方数的和等。而将一个给定的偶数分拆成两个素数之和，则被称之为此数的哥德巴赫分拆。例如，

4 = 2 + 2

6 = 3 + 3

8 = 3 + 5

10 = 3 + 7 = 5 + 5

12 = 5 + 7

14 = 3 + 11 = 7 + 7

…

换句话说，哥德巴赫猜想主张每个大于等于4的偶数都是哥德巴赫数——可表示成两个素数之和的数。哥德巴赫猜想也是二十世纪初希尔伯特第八问题中的一个子问题。

其实，也有一部分奇数可以用两个素数的和表示，大多数的奇数无法用两个素数的和表示，例如：15=2+13 ,而 23、35等数则无法用两素数的和表示。

哥德巴赫猜想在提出后的很长一段时间内毫无进展，直到二十世纪二十年代，数学家从组合数学与解析数论两方面分别提出了解决的思路，并在其后的半个世纪里取得了一系列突破。目前最好的结果是陈景润在1973年发表的陈氏定理（也被称为“1+2”）。

哥德巴赫猜想另一个较弱的版本（也称为弱哥德巴赫猜想）是声称大于5的奇数都可以表示成三个素数之和。这个猜想可以从哥德巴赫猜想推出。1937年，苏联数学家伊万·维诺格拉多夫证明了每个充分大的奇数，都可以表示成三个素数之和，基本证明了弱哥德巴赫猜想。

参考资料

哥德巴赫简介

欧拉与哥德巴赫之间的通信

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。