筹算
历史
筹算具体出现时间已然不可考,但根据典籍记录和考古发现,至少在战国初年筹算已然出现。它使用中国商代发明的十进位制计数,可以很方便地进行四则运算以及乘方,开方等较复杂运算,并可以对零、负数和分数作出表示与计算。
筹算在公元6世纪由中国传入朝鲜半岛和日本。七世纪的印度数学,分数中的分子在上,分母在下,与中国同,分数的乘除法也和《九章算术》相同。古印度数学绝大部分来自中国。 。一直到被珠算完全取代之前,筹算是东亚古代进行日常计算的方法,算筹是东亚古代数学家研究数学时常用的计算器具,是东亚古代各种重要数学发明的基础,开创了中国以至东亚古代以计算为中心的机械化数学体系,与古希腊以逻辑推理为中心的数学体系有所不同;机械化的数学体系是一千多年世界数学的主流
影响
筹算的乘除法传入印度,成为土盘算法 。9世纪初至10世纪,又经印度传入阿拉伯,这时期的阿拉伯阐述印度数学的数学著作,诸如《印度算术原理》,其土盘算式虽然用阿拉伯数字表示,但其十进位制概念,分数的表示法,以及加、减、乘、除四则运算的计算方法,和中国的筹算雷同,有的还用空格“ 0 ”表示“0”,和筹算一模一样。有学者认为,中国古代的筹算,通过丝绸之路传入印度、阿拉伯,促成印度-阿拉伯数字体系 。
数字表示

一到九的直型态与横型态对照
算筹数系是世界上唯一只用一个符号的方向和位置的组合,表示任何十进位数字或分数的系统。 单位数字:将筹棍竖排一根棍表示1,两根棍表示2,5根棍表示5如图上。但从6至9数字的表示,不是并排6至9根筹棍,而是采用同位五进制,即用一根筹棍代表数码5,横放在筹数1至4的上方如图。这已蕴含算盘雏形。上排是筹算中1至9的竖码,下排是相应数字的横码。

使用直横排列避免混淆
大于9的数字,则用十进制表示,在个位数的位置左边,放置一个筹数,代表这个筹数的十倍,在十位数值左的位置,代表百位数,如此类推。如图所示数二百三十一(231)的表示法,在个位放置一根筹码,表示1,在十位放置筹数3,代表30,在百位放置筹数2,代表200,总数即二百三十一(231)。《孙子算经》云:
。
筹算板一般是桌面或地面,通常没有格子。如果筹码2,3,1并排排列,有可能被误读为51或24;为了避免邻位误读,先民发明了每隔一位交替使用竖码横码,即个位竖码,十位用横码,百位用竖码,千位用横码,如此类推,就可以完全避免误读了 。
零的表示
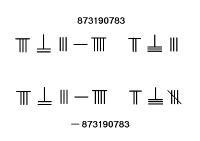
数字后加斜棍表负数
中国自有筹算起就有“0”,即以空位表示“0”。筹算中的零是位置零和运算结果的零,没有特定符号,这和阿拉伯数字专有一个符号0不同, 阿拉伯数字0只是符号零,不是运算结果。
正负数
宋代数学家用红色筹码代表正数,用黑色筹码代表负数,也有一律用黑色筹码,但在数字最后一位加一根斜棍标示为负数。
小数
孙子算经的度量衡已有十进位制概念,如尺、寸、分、厘、毫、丝、忽。七丈一尺二寸三分四厘五毫六丝,用现代表示方法为71.23456尺,用算筹排为
其中 为十位数, 为个位数, 为十分之一位等等。
南宋秦九韶在《数书九章》中将小数推广到非度量衡,如
表示为:
即在个位数1下记一“日”字。
加法
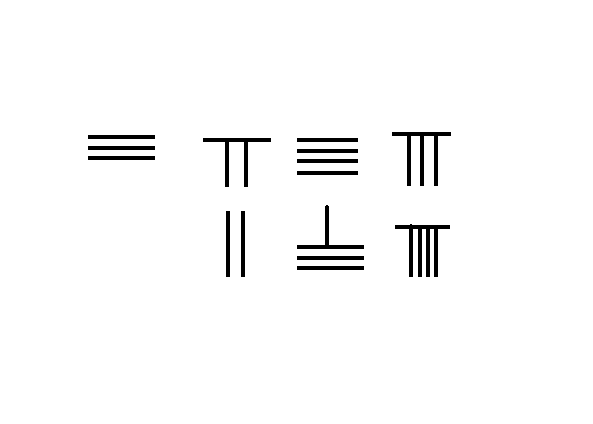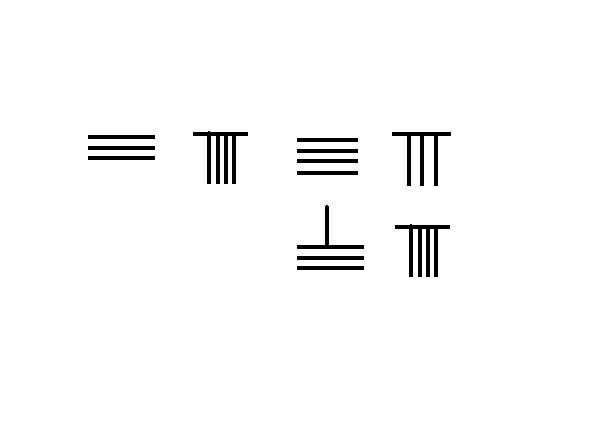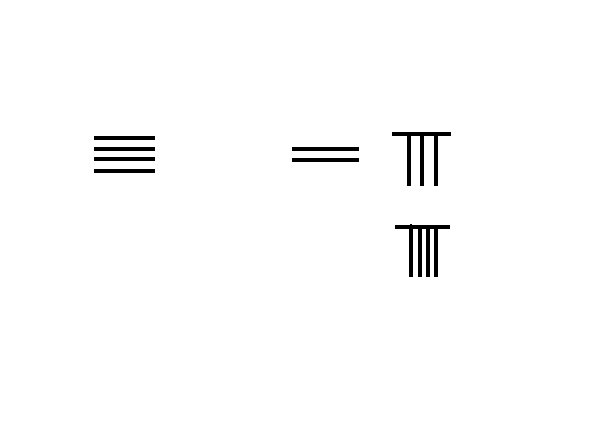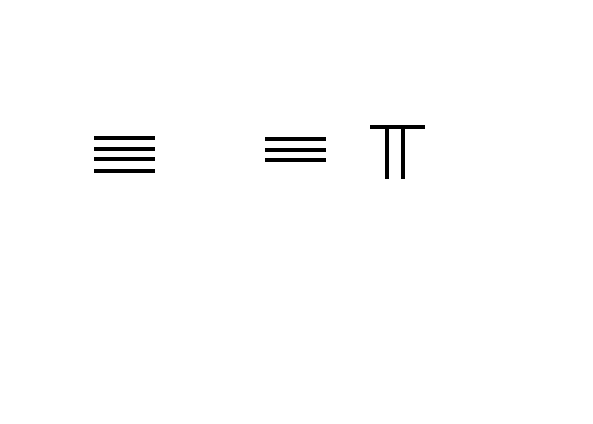
筹算加法 3748 + 289 = 4037 {\displaystyle 3748+289=4037}

算筹本身已经包含加法,因此用算筹进行加法运算十分方便快捷。筹算加法与阿拉伯数字加法最大的不同,在于算筹本身具有可加性,用算筹进行加法运算,只须机械地搬动筹棍,即可进行运算,不需要另外背诵加法表,这与阿拉伯数字不同,不可能将阿拉伯数字1和2机械地叠成3字,2和3叠成一个5字。
左图表示 3748 + 289 {\displaystyle 3748+289} 的运筹步骤:
将被加数3748放上行,加数289放下行,位数对齐。
从左往右计算。
取出下行百位数的二竖棍,与上行7合并为9。
从上行十位的4,取出二根筹棍(上行剩2),与下行8合为10,进位1,与百位的9合为10,进一位。
将个位数的8,取出一根筹与下行9合为10,进位1,与百位的2合为3
答案4037。
上行被加数筹码,在运算过程中逐步变化;下行加数筹码,在运算过程中逐步消失。
减法
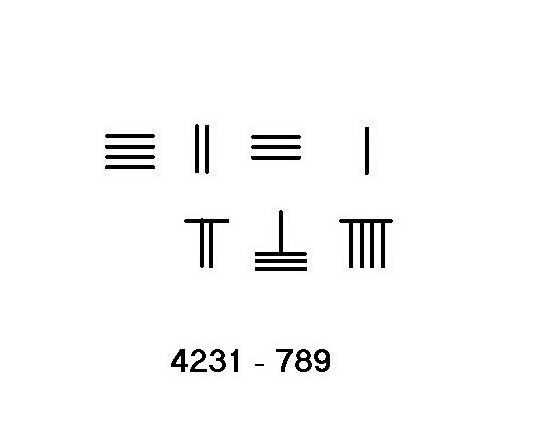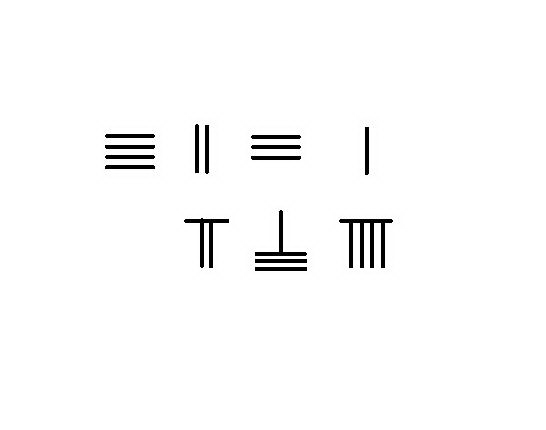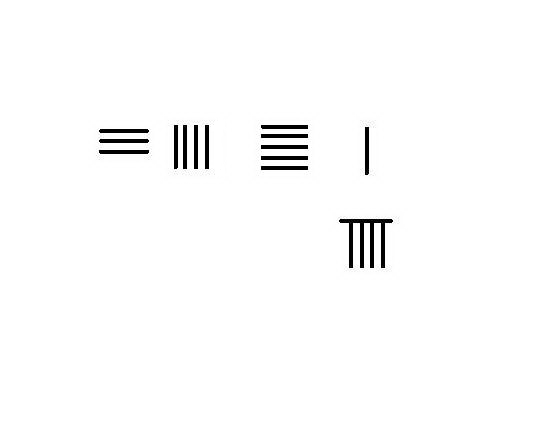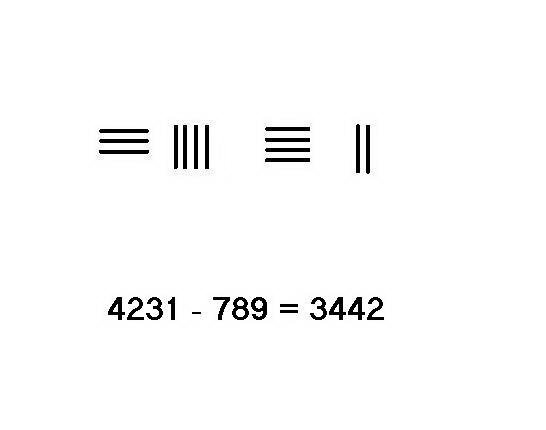
不需向上一数量级借位的情况下,只要从被减数中去掉与减数相同数目的筹棍,剩余的筹码就是答案。左图为计算54-23的演示步骤。 右图为计算4231-789的演示步骤,此情况即为需要向上一数量级借位:
将被减数4231放在上行,减数789放下行。从左往右逐位运筹。
从千位借1为百位10,减去下行该位的7,余数3与上行2合为5,下行本位的7被取去,留空白。
从百位5借1留4,百位所借1减十位下行8得2,与上行3合为5;至此上行筹码为3451,下行为9。
从上行十位的5借1余四,所借1(=10)减去下行9得1,搬往上行得2,至此下行筹码已全部减除,上行得3442即是运算结果。
乘法
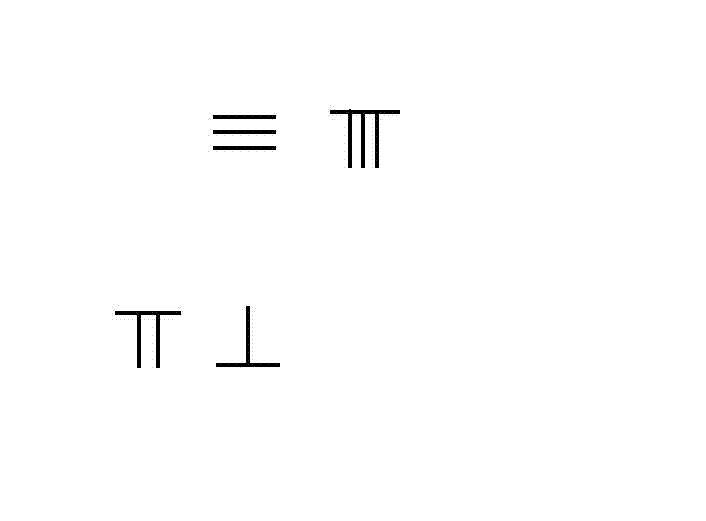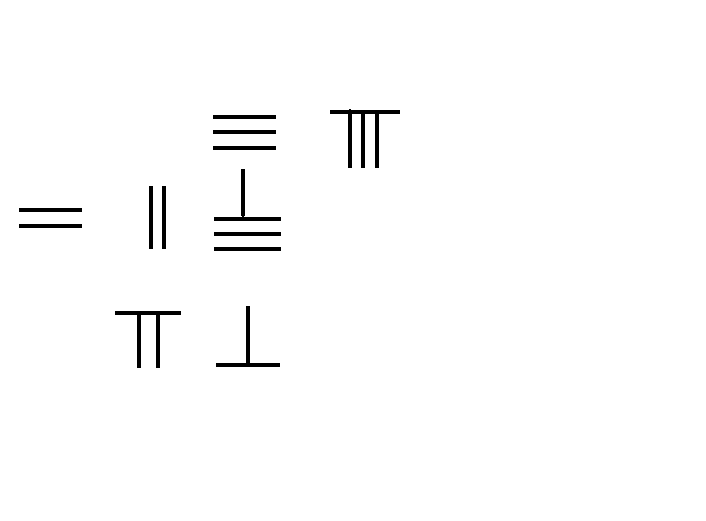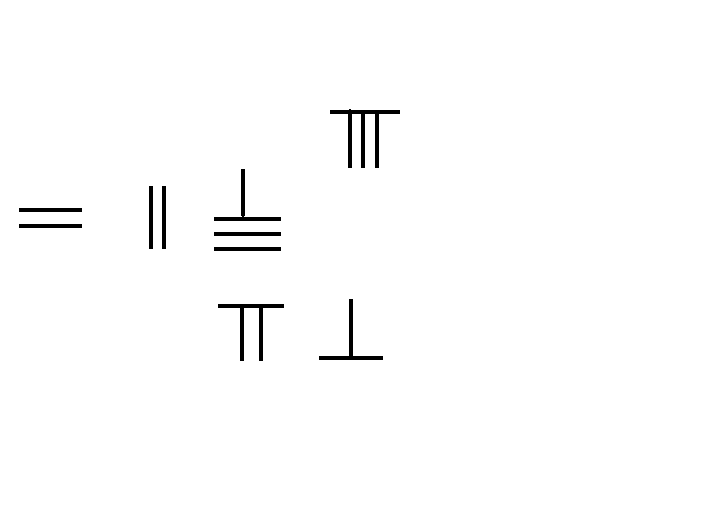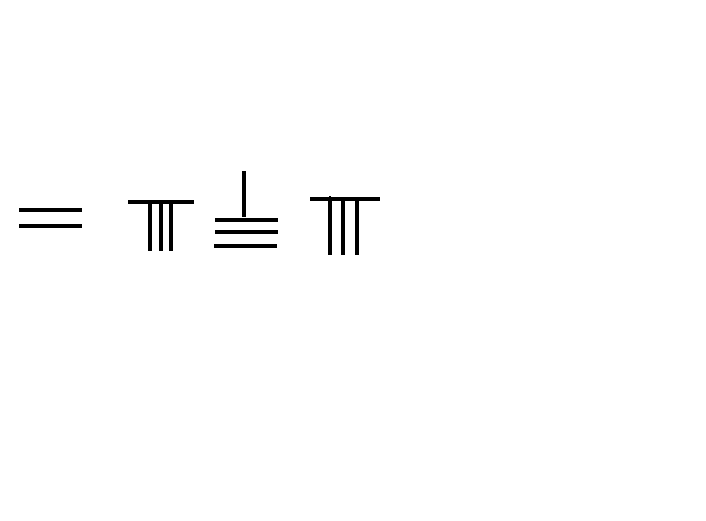
筹算 38x76=2888

十世纪阿拉伯数学家阿尔乌基里德的乘法,是孙子乘法的变化
运用算筹进行乘除运算时必须先学会九九表:《夏侯阳算经》云:
《孙子算经》对筹算乘法有详细阐述。 左图即为筹算38×76的演示步骤:
将被乘数放在上排(上位),乘数放在下排(下位),乘数的个位,对齐被乘数的最高位。如图:被乘数38在上排,乘数76在下排,其个位数6对齐被乘数38的3。上下排之间,留空几排,作中间积存放处。
运算规则:从左至右。
从被乘数的最高位开始运筹(例中即先运算30×76,再运算8×76)。在运算中必须运用九九表。据九九表“三七二十一”,将筹码21放在中间排,1对齐乘数的十位,即在7之上;然后“三六一十八”;(30×76得中间积2280),如图中排,至此被乘数的3已经完成运算,从筹板除去。
将乘数76的筹码,往右移动一位,7改横码,6改为竖码;
以下再运算8×76,运算“七八五十六”,撤乘数十位数筹码7;
运算“八十八”,4与上一步所得56的6合并为10,进位1,撤去被乘数个位8,撤去乘数个位6;
将中间积2280与608相加,得积2888,至此整条算式运算完毕。
P.S.:范例图片是一边乘一边加而不是像文字描述所说乘完后才加。
除法
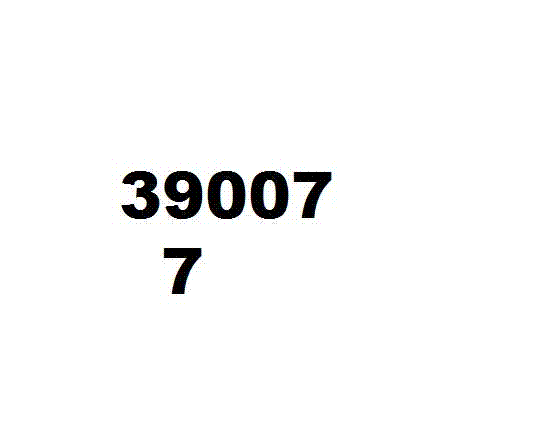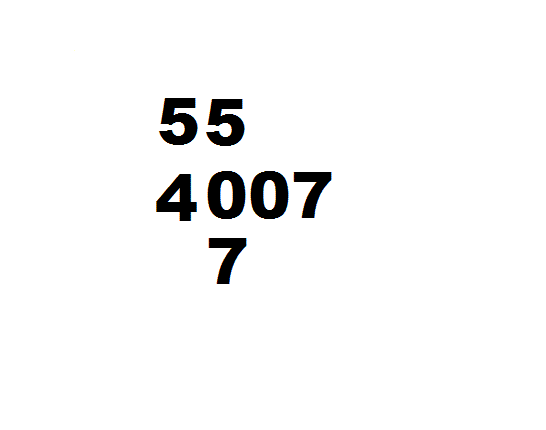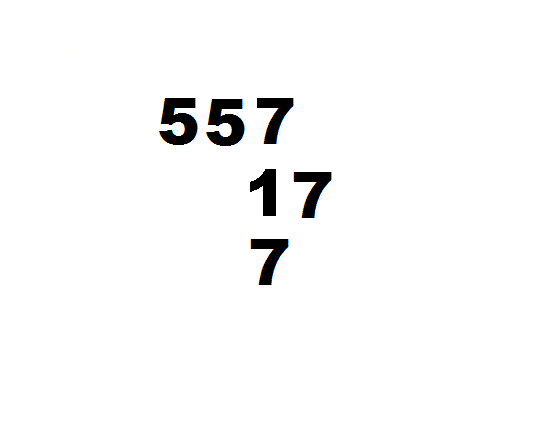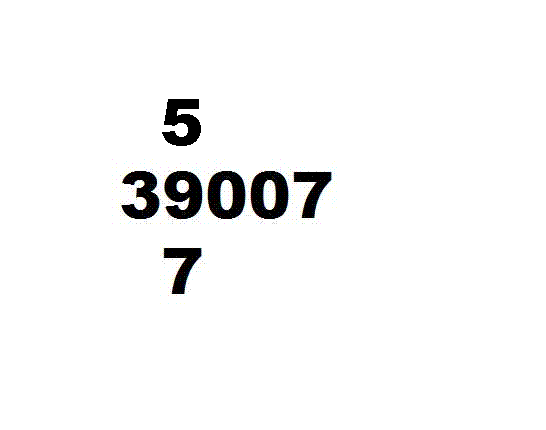
十世纪阿尔乌几里德除法
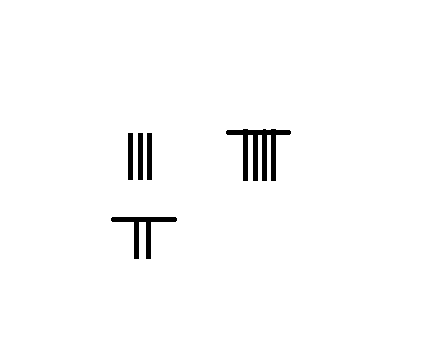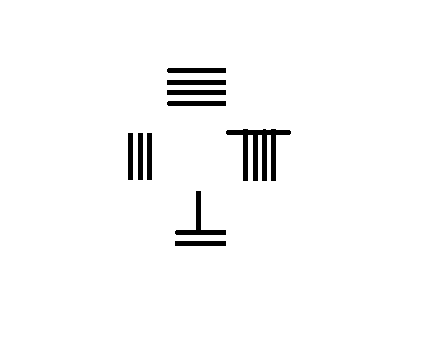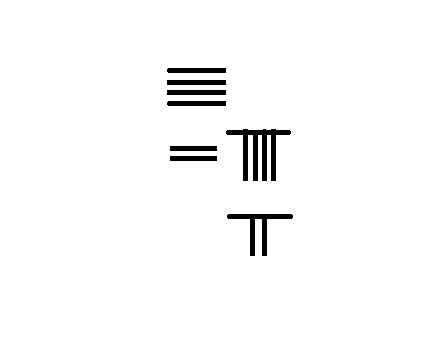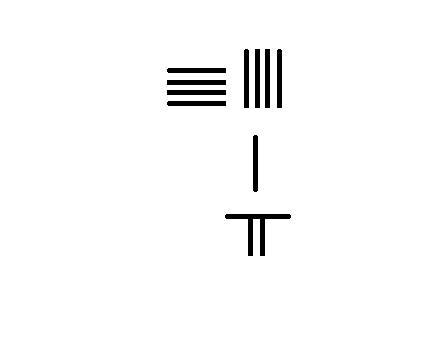
孙子除法 309/7=44 1/7
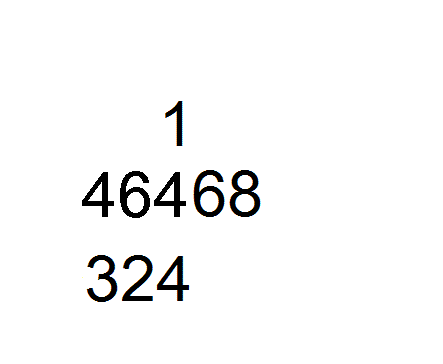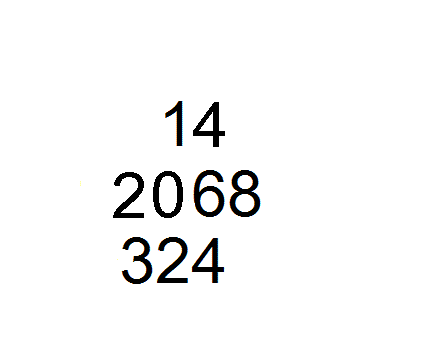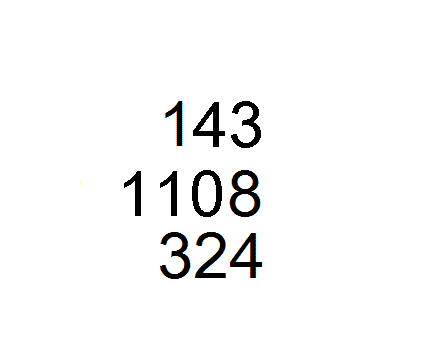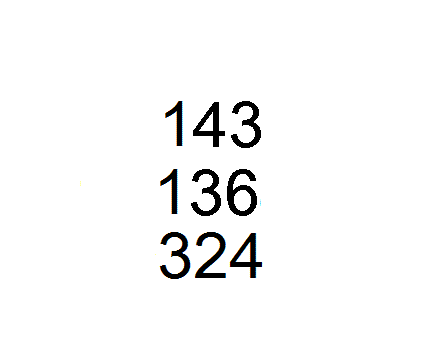
9世纪花拉子米除法是孙子除法的翻版
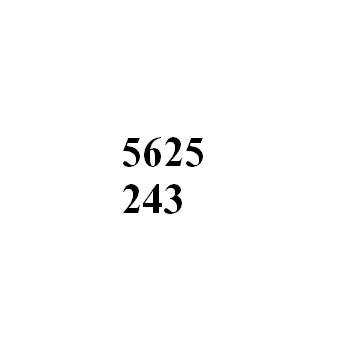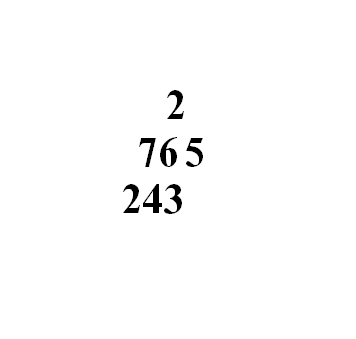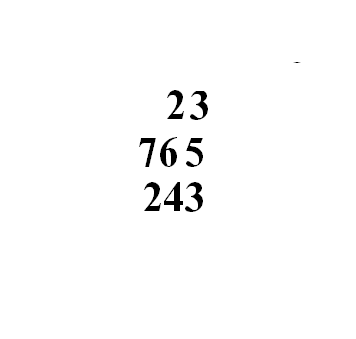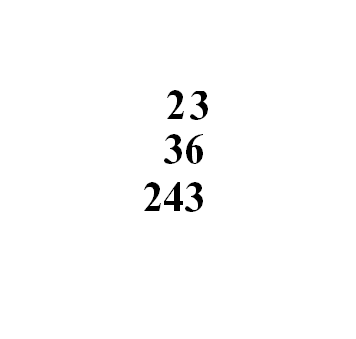
十一世纪伊本·拉班除法也是孙子除法的翻版
左图为计算 309 7 {\displaystyle {\frac {309}{7}}} 的演示步骤:
将被除数309放中排,除数7放下排,上排留空。
将除数7左移一位,变横码,用九九表和减法运算30÷7:30除7得4剩2,
商4摆上排,2留中排。
将除数7右移一位,改竖码;再用九九表和减法运算29÷7:29除7得4余1,
商4放上排,除数不撤,最后得商44,余数1,故 309 7 = 44 1 7 {\displaystyle {\frac {309}{7}}=44{\frac {1}{7}}} 。
孙子除法在9世纪初最早由花拉子米从印度介绍到阿拉伯国家,十世纪阿拉伯数学家阿尔乌几里德《印度的算术》 叙述的早期除法和十一世纪波斯数学家伊本·拉班《印度算术原理》叙述的除法,也是不折不扣的孙子除法:
同样上、中、下三行的布列格式
同样上为商数,中为被除数,下为除数
同样的左边对齐
同样的自左往右运算
同样算一步后将除数右移一位
同样除数后面以空格代0
同样的商和余数,以三行格式表示。
分数
用筹算进行除法运算时,如留有余数,则必须保留除数和余数,形成一对筹码,一在上一在下。刘徽《九章算术注》中,在上的筹称“实”,为在下的筹称为“法”:《孙子算经》中,在上的筹称为“子”,(分子),而在下的称为“母”(分母)。如右图一对筹码一在上一在下,1是子,7是母,构成分数 1 7 {\displaystyle {\frac {1}{7}}} 。 这种筹算分数的表示法,在9世纪由花拉子米介绍到阿拉伯国家。
分数加法
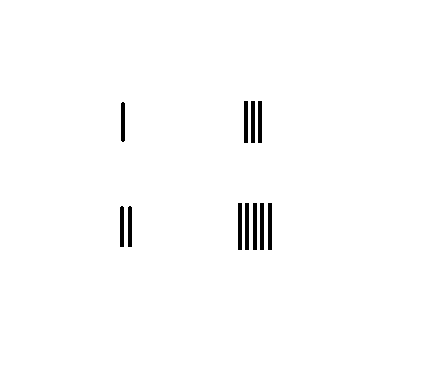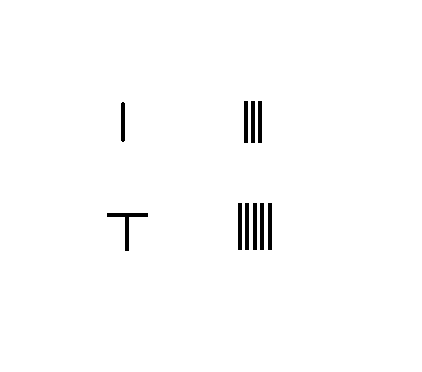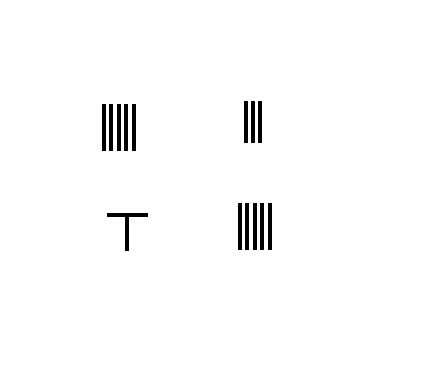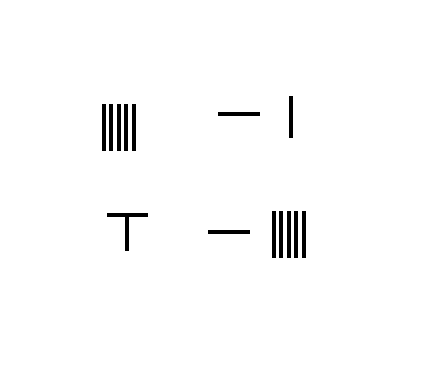
分数加法
1 3 + 2 5 {\displaystyle {\frac {1}{3}}+{\frac {2}{5}}}
将分子1,2 摆放在算筹板的左边,将分母3,5摆放在算筹板的右边
将分子与分母交叉互乘,将所得的积代替相应的分子
将分母相乘,将乘积摆放在算筹板右下方
将新的分子相加,其和摆放在算筹板右上方
结果: 1 3 + 2 5 {\displaystyle {\frac {1}{3}}+{\frac {2}{5}}} = 11 15 {\displaystyle {\frac {11}{15}}}
分数减法

分数减法
8 9 − − --> 1 5 {\displaystyle {\frac {8}{9}}-{\frac {1}{5}}}
将分子8,1的算筹摆放在算筹板的左边
将分母9,5 摆放在算筹板的右边
分子分母互乘,以乘积代替相应的分子。
分母相乘,其积摆放在算筹板右下方
新分子相减为差,将差数摆放在算筹板右上方
结果: 8 9 − − --> 1 5 {\displaystyle {\frac {8}{9}}-{\frac {1}{5}}} = 31 45 {\displaystyle {\frac {31}{45}}}
分数乘法
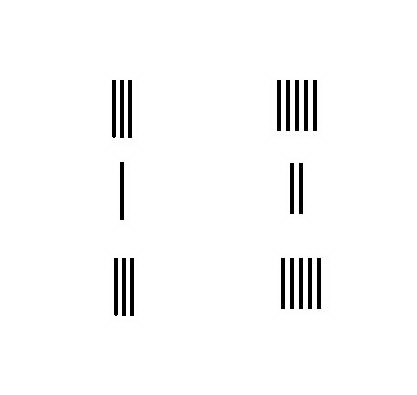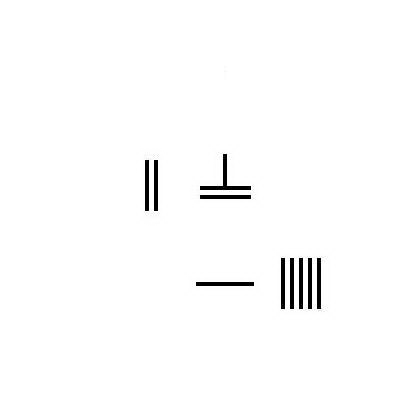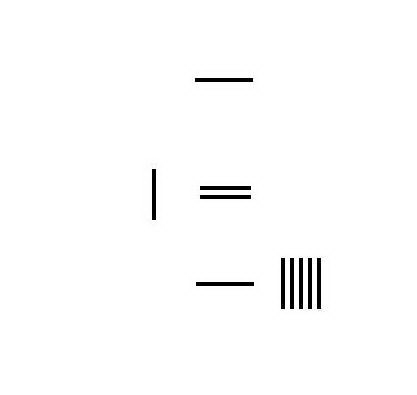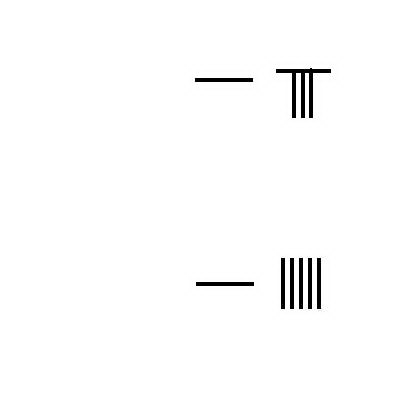
分数乘法
3 1 3 × × --> 5 2 5 {\displaystyle 3{\frac {1}{3}}\times 5{\frac {2}{5}}}
将 3 1 3 {\displaystyle 3{\frac {1}{3}}} 和 2 5 {\displaystyle {\frac {2}{5}}} 在算筹板上布置成商、实、法形式。
商乘法加入实。 3*3 + 1=10; 5*5 + 2=27
实乘实:10*27=270
法乘法:3*5=15
实除法: 3 1 3 × × --> 5 2 5 {\displaystyle 3{\frac {1}{3}}\times 5{\frac {2}{5}}} =18
分数除法
将分数在算筹板上以商、实、法的三行格式排列。
将商乘法,并入实。
将除数分数的分子、分母互换。
分子、分母相乘。
约分。
最大公约数
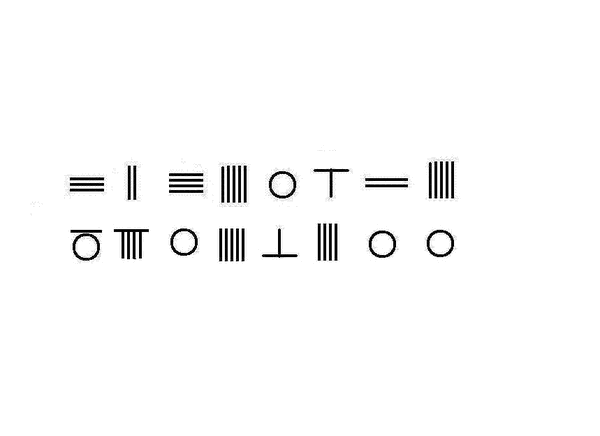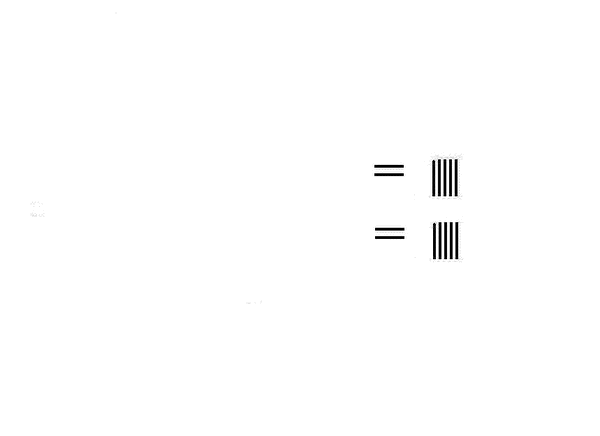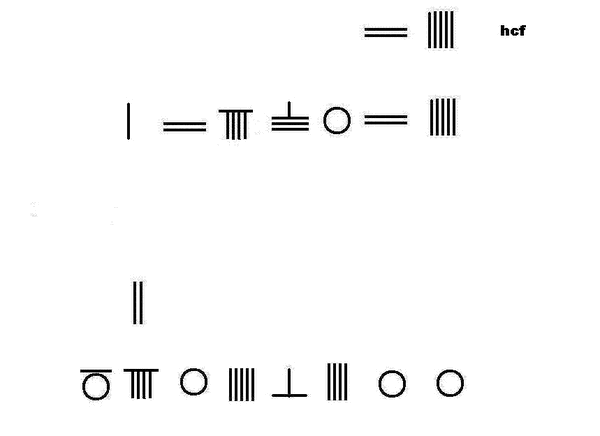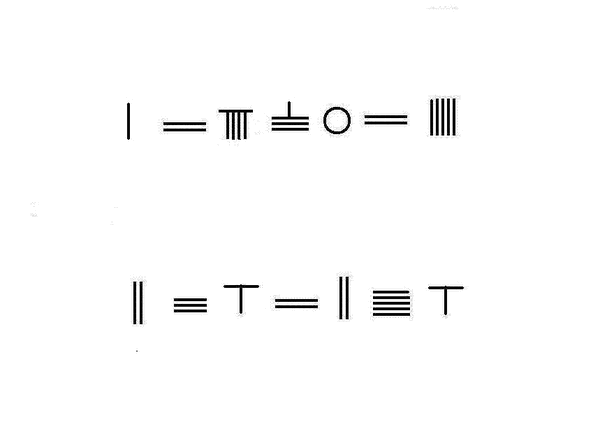
求最大公约数
九章算术给出求两个数最大公约数的方法,即辗转相除,以至最后余数相等,即为最大公约数。
左图为求 32450625 59056400 {\displaystyle {\frac {32450625}{59056400}}} 的最大公约数,并进行约分。
最大公约数为25,约分得 1298025 2362256 {\displaystyle {\frac {1298025}{2362256}}} 。
分数内插法
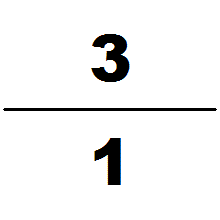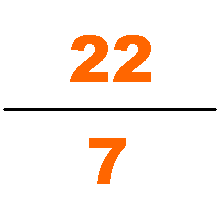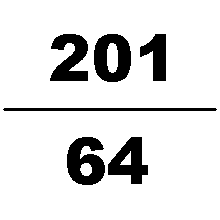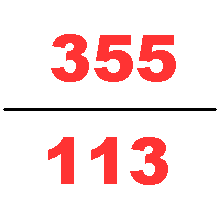
何承天发明名为调日法的分数内插法,反复将弱值分数与强值分数的分子分母相加已求得更佳的近似值。祖冲之用此法求的著名的圆周率 约率 22 7 {\displaystyle {\frac {22}{7}}} 和密率 355 113 {\displaystyle {\frac {355}{113}}}
开平方根
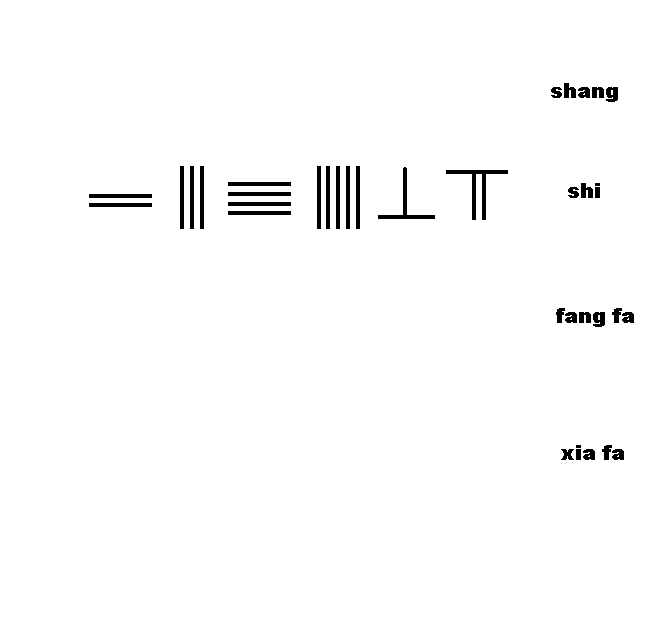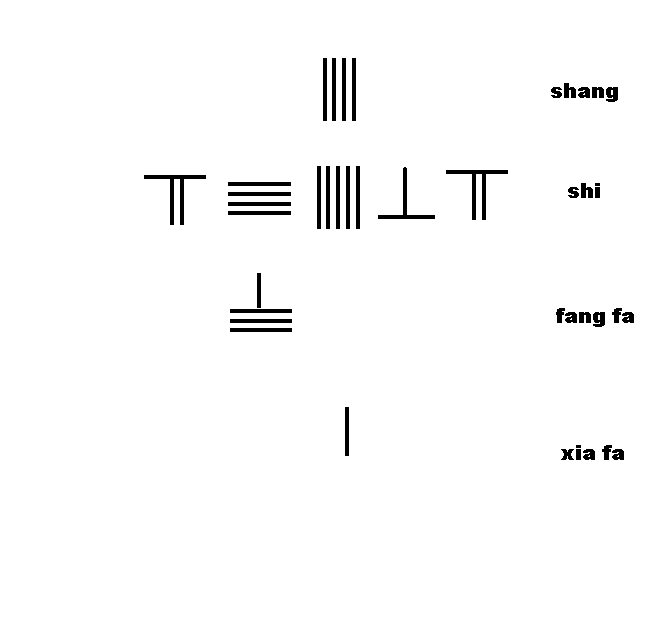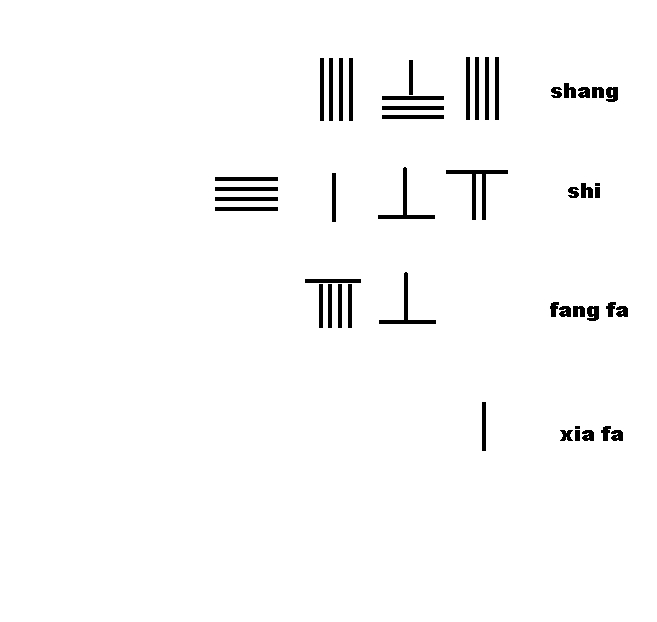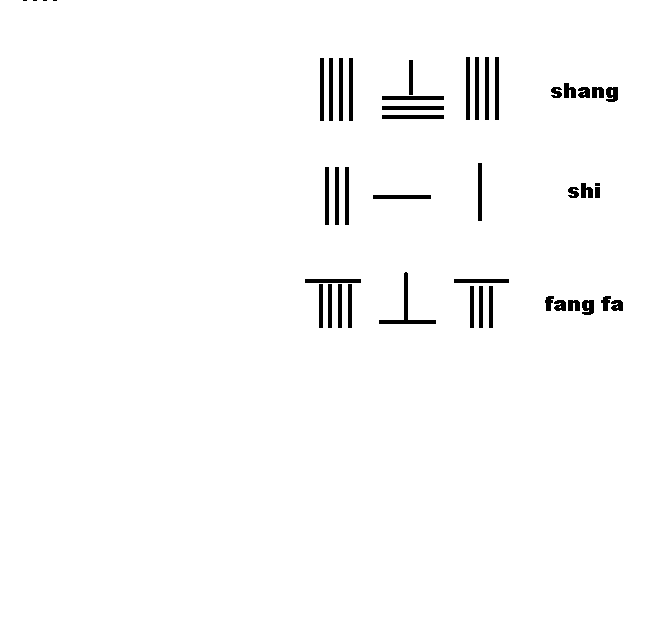
筹算开方术

伊本·拉班开平方术
孙子算经卷中:“今有积,二十三万四千五百六十七步。问:为方几何?答曰:四百八十四步九百六十八分步之三百一十一。
术曰:置积二十三万四千五百六十七步,为实,次借一算为下法,步之超一位至百而止。上商置四百于实之上,副置四万于实之下。下法之商,名为方法;命上商四百除实,除讫,倍方法,方法一退,下法再退,复置上商八十以次前商,副置八百于方法之下。下法之上,名为廉法;方廉各命上商八十以除实,除讫,倍廉法,从方法,方法一退,下法再退,复置上商四以次前,副置四于方法之下。下法之上,名曰隅法;方廉隅各命上商四以除实,除讫,倍隅法,从方法,上商得四百八十四,下法得九百六十八,不尽三百一十一,是为方四百八十四步九百六十八分步之三百一十一”。
右图为筹算开方 234567 ≈ ≈ --> 484 311 968 {\displaystyle {\sqrt {234567}}\approx 484{\tfrac {311}{968}}} 。
算法如下:
把234567放在算筹板的由上数起的第二行上,称之为 实 。
把一个标记“1”放置在第四行的万位,称为 下法 。
估计平方根的第一位,放在第一行( 商 )的百位。
将商乘以下法(4×1),把积放在第三行,称之为 方法 。
将实减去商和方法的积,23-4×4=7
将方法乘以2,把它移向右边,改为横码。
把下法向右移两位。
估计平方根的第二位,放在商的十位。
将商乘以下法,积加到方法。
8×8=64,将74减去64,把10放到实。
把方法的个位乘以2,加到原方法80。
把方法向右移,改变方向;把下法向右移两位。
估计平方根的第三位。
将商乘以下法(4×1),积加到方法,此时方法应为964。
从实减去4×9+4×6+4×4=76,余下311。
把方法的个位乘以2,加到原方法960。
答案: 234567 ≈ ≈ --> 484 311 968 {\displaystyle {\sqrt {234567}}\approx 484{\tfrac {311}{968}}}
十一世纪波斯数学家伊本·拉班的开平方术,与孙子基本上向同,唯最后分母加1,所以平方根的小数比真值略小,孙子算法所得,则比真值略大。
开立方根
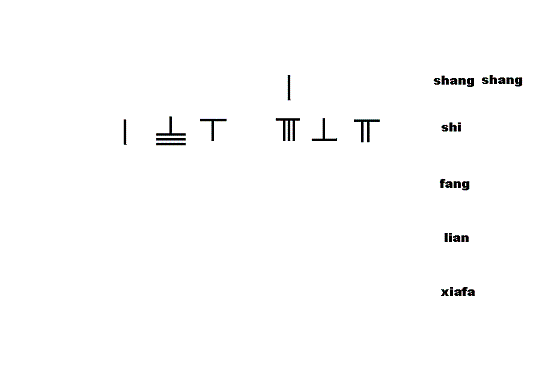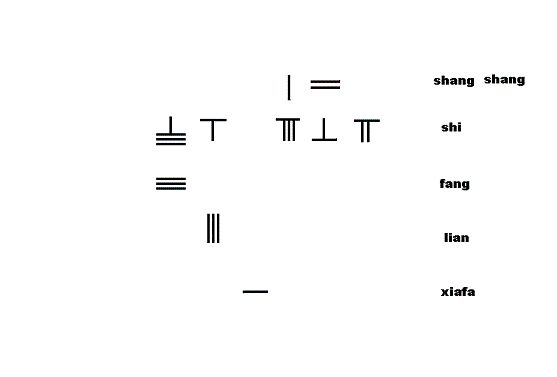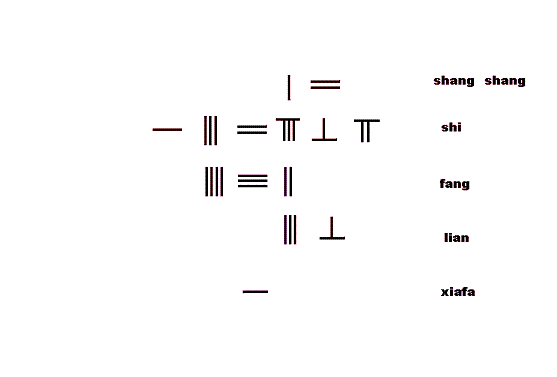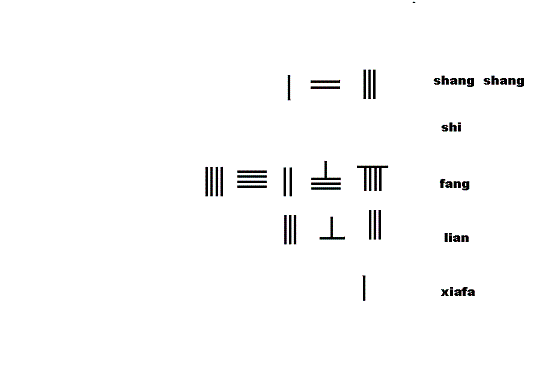
贾宪增乘开立方术
九章算术卷第四《少广》有数道开立方题,其开立方术为后世开立方术的基础。
〔二二〕又有积一百九十三万七千五百四十一尺、二十七分尺之一十七。问为立方几何?
答曰:一百二十四尺、太半尺。 开立方术曰:置积为实。借一算步之,超二等。议所得,以再乘所借一算为法,而除之。除已,三之为定法。复除,折而下。以三乘所得数置中行。复借一算置下行。步之,中超一,下超二等。复置议,以一乘中,再乘下,皆副以加定法。以定法除。除已,倍下、并中从定法。复除,折下如前。开之不尽者,亦为不可开。若积有分者,通分内子为定实。定实乃开之,讫,开其母以报除。若母不可开者,又以母再乘定实,乃开之。讫,令如母而一。
1937541 17 27 3 = 124 2 3 {\displaystyle {\sqrt[{3}]{1937541{\frac {17}{27}}}}=124{\frac {2}{3}}}
北宋数学家贾宪发明增乘开立方法和递增三乘开四次方术。
右图为贾宪增乘开立方解九章算术第四卷少广〔一九〕
今有积一百八十六万八百六十七尺。问为立方几何?
答曰:一百二十三尺。
: 1860867 3 = 123 {\displaystyle {\sqrt[{3}]{1860867}}=123}
联立方程
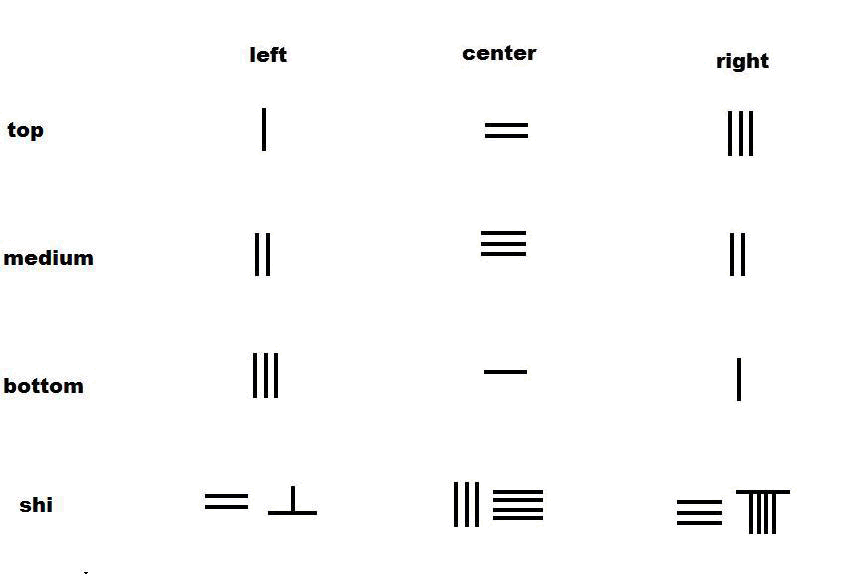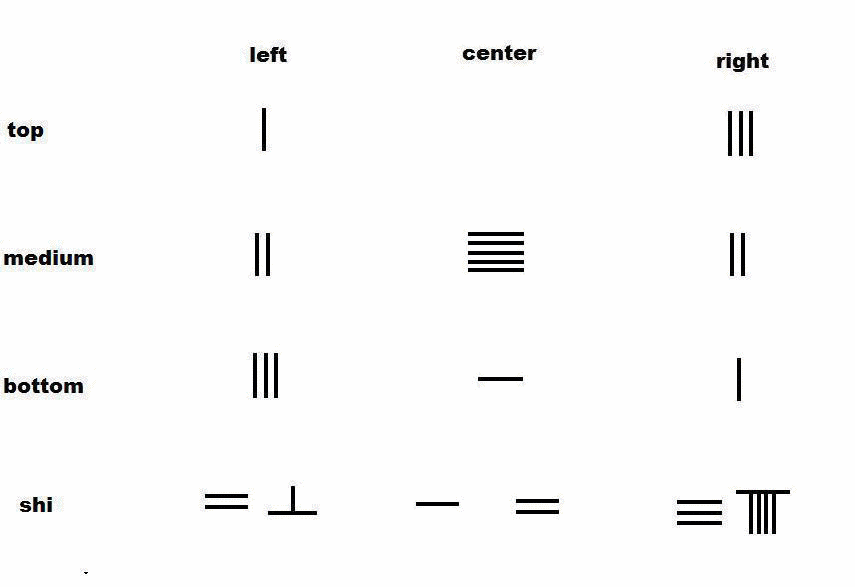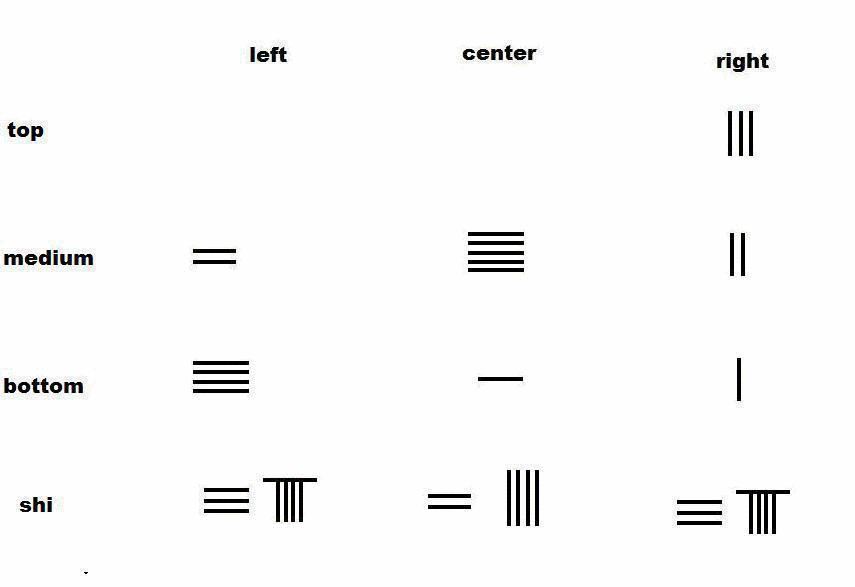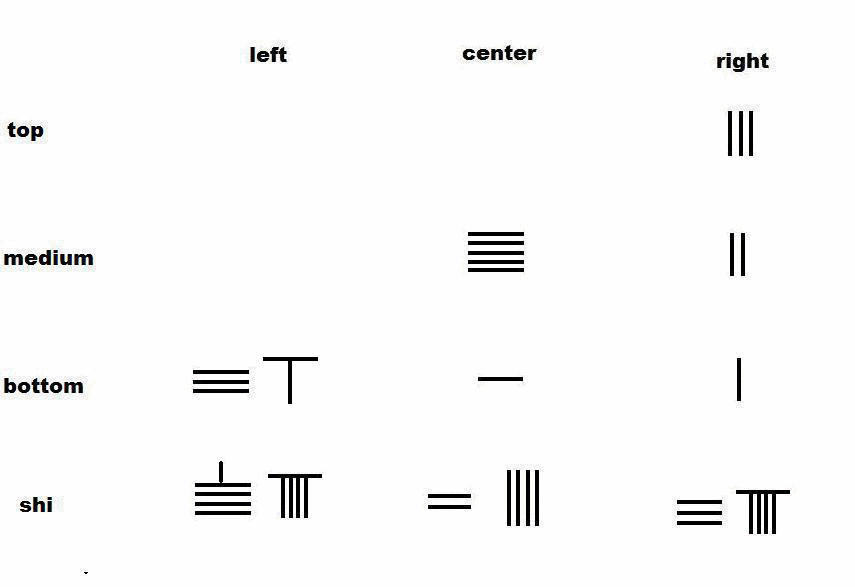
联立方程
九章算术 卷第八 方程: 〔一〕今有上禾三秉,中禾二秉,下禾一秉,实三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉,中禾二秉,下禾三秉,实二十六斗。 问上、中、下禾实一秉各几何?
答曰:
上禾一秉,九斗、四分斗之一,
中禾一秉,四斗、四分斗之一,
下禾一秉,二斗、四分斗之三。
有三捆上等谷物,两捆中等谷物,一捆下等谷物,共39斗;有两捆上等,三捆中等,一捆下等,共34斗;有一捆上等,两捆中等,三捆下等,共26斗。分别找出上、中、下等谷物的数量。
方程术曰,置上禾三秉,中禾二秉,下禾一秉,实三十九斗,于右方。中、左禾列如右方。
以右行上禾遍乘中行而以直除。又乘其次,亦以直除。然以中行中禾不尽者遍乘左行而以直除。左方下禾不尽者,上为法,下为实。实即下禾之实。求中禾,以法乘中行下实,而除下禾之实。余如中禾秉数而一,即中禾之实。求上禾亦以法乘右行下实,而除下禾、中禾之实。余如上禾秉数而一,即上禾之实。实皆如法,各得一斗。
将中列乘以右上角的数字,即3。
重复地从中列减去右列,直到中上角的数字为0。
将左列乘以右上角的数字,即3。
重复地从左列减去右列,直到左上角的数字为0。
对中列和左列使用上述消除算法后,矩阵将简化成三角形状:
一捆下等谷物的数量= 99 36 = 2 3 4 {\displaystyle {\frac {99}{36}}=2{\frac {3}{4}}} 斗
一捆上等谷物= 9 1 4 {\displaystyle 9{\frac {1}{4}}} 斗
一捆中等谷物= 4 1 4 {\displaystyle 4{\frac {1}{4}}} 斗
行列式
日本数学家关孝和在《三部抄》的《解伏题之法》中,将线性方程组的系数纵横写成方阵的形式,发明了行列式。关孝和还提出了两种计算行列式的值的方法:逐式交乘法和交式斜乘法。
高次方程
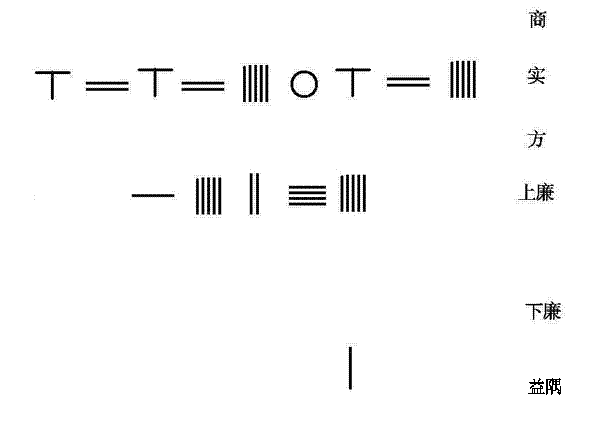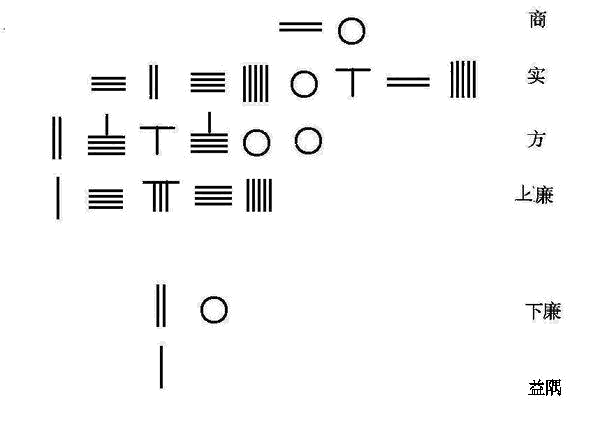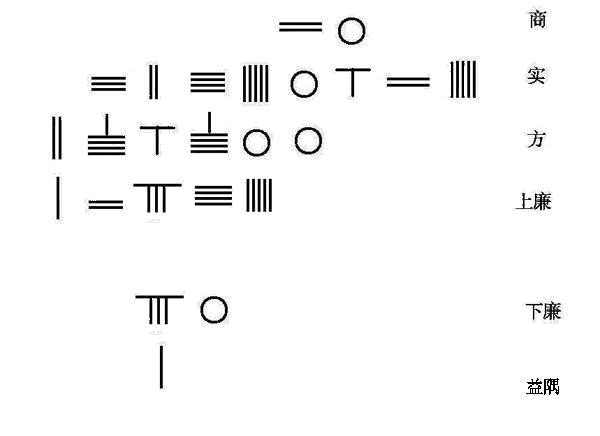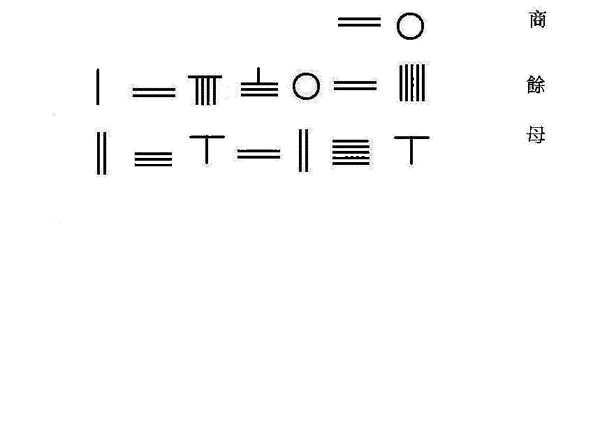
南宋数学家秦九韶将贾宪的增乘开方术推广,以求解高次方程。右图为秦九韶解下列四次方程式的程序。
程序:
置6262506.25 为实
置15245 为上廉
置1为益隅
上廉超二位,益隅超三位。
置商20步
以商乘益隅入下廉
以下廉乘商生负廉
以负廉与正廉相消得正上廉
以商乘上廉为方
以方乘商除实
又以商乘益隅入下廉
以下廉乘商生负廉
负廉与正廉相消
商与上廉生方
商隅相乘入下廉
商与下廉生负廉
负廉与正廉相消
商又与隅生下廉
下廉三退,隅四退
无商(商第二位为0),以上廉并入方,并益隅入下廉
益隅并负廉与正方廉相消,命为母
约分
得 x = 20 1298025 2362256 {\displaystyle x=20{\frac {1298025}{2362256}}}
四元高次方程
筹算的应用在朱世杰《四元玉鉴》中的四元术到达高峰。
今有股弦较除弦和与直积等。只云勾股较除弦较和与勾同。问弦几何?
:得到 今式 − − --> y − − --> z − − --> y 2 × × --> x − − --> x + x y z = 0 {\displaystyle -y-z-y^{2}\times x-x+xyz=0}
云式: − − --> y − − --> z + x − − --> x 2 + x z = 0 {\displaystyle -y-z+x-x^{2}+xz=0}
三元式: y 2 − − --> z 2 + x 2 = 0 ; {\displaystyle y^{2}-z^{2}+x^{2}=0;}
三元式与云式相消,
人天易位 人弦-->天勾
得: 前式 − − --> x − − --> 2 x 2 + y + y 2 + x y − − --> x y 2 + x 2 y {\displaystyle -x-2x^{2}+y+y^{2}+xy-xy^{2}+x^{2}y}
及 后式 − − --> 2 x − − --> 2 x 2 + 2 y − − --> 2 y 2 + y 3 + 4 x y − − --> 2 x y 2 + x y 2 {\displaystyle -2x-2x^{2}+2y-2y^{2}+y^{3}+4xy-2xy^{2}+xy^{2}}
相消得 x 4 − − --> 6 x 3 + 4 x 2 + 6 x − − --> 6 = 0 {\displaystyle x^{4}-6x^{3}+4x^{2}+6x-6=0}
解之得 x = 5 {\displaystyle x=5} 天勾=5;
人天易位 天勾-->人弦
得弦=五步。

朱世杰《四元玉鉴·四象会元》四元术
今有股乘五较与弦幂加勾乘弦等。只云勾除五和与股幂减勾弦同。问黄方带勾股弦共几何?
消元,物易天位
解之,
物易天位,得 十四步。
参看
增乘开平方法
参考文献
^ 钱宝琮 《中国古代分数算法的发展》 《李俨.钱宝琮科学史全集》卷9 392页
^ 吴文俊 《中国古代数学对世界文化的伟大贡献》 《吴文俊文集》 2页
^ 钱宝琮 《中国古代数学的伟大成就》 《李俨.钱宝琮科学史全集》卷9 383页
^新加坡大学教授蓝丽蓉:《阿拉伯数字体系起源于中国筹算的证据》,Fleeting Footsteps
^李约瑟原著 柯林‧罗南改编《中华科学文明史》卷2 第一章 数学
^ Ho Peng Yoke, Li, Qi and Shu p58 ISBN 0-486-41445-0
^ Lam Lay Yong, p87-88
^ Abu al-Hasan Ahmad ibn Ibrahim al-Uqlidisi, The Arithematics of Al-Uqlidisi, tran. A.S.Saidan, P57 D.Reidel, Boston, USA 1978
^ 朱世杰原著 李兆华校正 《四元玉鉴》 153页 ISBN 978-7-03-020112-6
^ 《李俨钱宝琮科学史全集》 第一卷李俨《中国算学史》 第435-439页
吴文俊主编 《中国数学史大系·第四卷》第一章 《孙子算经》 第三节 算筹与筹算 北京师范大学出版社 ISBN:7303049258
《九章算术白话译解》 重庆大学出版社 ISBN 7-5624-3848-X
李约瑟原著 柯林·罗南改编《中华科学文明史》卷2 第一章 数学
Lam Lay Yong(兰丽蓉) Ang Tian Se(洪天赐), Fleeting Footsteps, World Scientific ISBN 981-02-3696-4
Ho Peng Yoke, Li, Qi and Shu ISBN 0-486-41445-0
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。

相关资料

- 有价值
- 一般般
- 没价值








24小时热门
推荐阅读
关于我们

APP下载




























{{item.time}} {{item.replyListShow ? '收起' : '展开'}}评论 {{curReplyId == item.id ? '取消回复' : '回复'}}