洛伦兹变换的提出

19世纪后期建立了麦克斯韦方程组，标志着经典电动力学取得了巨大成功。然而麦克斯韦方程组在经典力学的伽利略变换下并不是协变的。

由麦克斯韦方程组可以得到电磁波的波动方程，由波动方程解出真空中的光速是一个常数。按照经典力学的时空观，这个结论应当只在某个特定的惯性参照系中成立，这个参照系就是以太。其它参照系中测量到的光速是以太中光速与观察者所在参照系相对以太参照系的速度的矢量叠加。然而1887年的迈克耳孙-莫雷实验测量不到地球相对于以太参照系的运动速度。1904年，洛伦兹提出了洛伦兹变换用于解释迈克耳孙-莫雷实验的结果。根据他的设想，观察者相对于以太以一定速度运动时，长度在运动方向上发生收缩，抵消了不同方向上由于光速差异，这样就解释了迈克耳孙-莫雷实验的零结果。

洛伦兹变换的数学形式

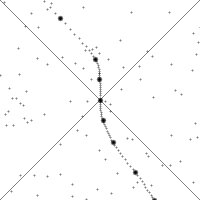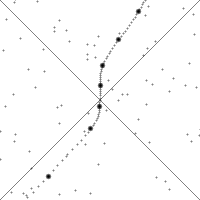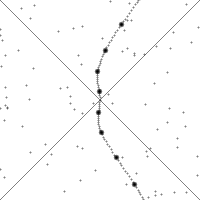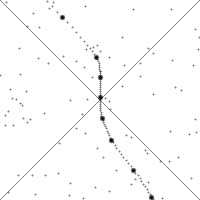
沿着快速加速的观察者的世界线来看的时空。 竖直方向表示时间。水平方向表示距离，虚划线是观察者的时空轨迹（“世界线”）。图的下四分之一表示观察者可以看到的事件。上四分之一表示光锥- 将可以看到观察者的事件点。小点是时空中的任意的事件。 世界线的斜率（从竖直方向的偏离）给出了相对于观察者的速度。注意看时空的图像随着观察者加速时的变化。

洛伦兹提出洛伦兹变换是基于以太存在的前提的，然而以太被证实是不存在的，根据光速不变原理，相对于任何惯性参照系，光速都具有相同的数值。爱因斯坦据此提出了狭义相对论。在狭义相对论中，空间和时间并不相互独立，而是一个统一的四维时空整体，不同惯性参照系之间的变换关系式与洛伦兹变换在数学表达式上是一致的，即：

其中x、y、z、t分别是惯性坐标系Σ下的坐标和时间，x"、y"、z"、t"分别是惯性坐标系Σ"下的坐标和时间。v是Σ"坐标系相对于Σ坐标系的运动速度，方向沿x轴。

由狭义相对性原理，只需在上述洛伦兹变换中把v变成-v，x"、y"、z"、t"分别与x、y、z、t互换，就得到洛伦兹变换的反变换式：

洛伦兹变换是高速运动的宏观物体在不同惯性参照系之间进行坐标和时间变换的基本规律。当相对速度v远远小于光速c时，洛伦兹变换退化为经典力学中的伽利略变换:

所以，狭义相对论与经典力学并不矛盾，狭义相对论将经典力学扩展到了宏观物体在一切运动速度下的普遍情况，经典力学只是相对论在低速时（v远远小于c）的近似情况。一般在处理运动速度不太高的物体时（如天体力学中计算行星的运行轨道），不需考虑到相对论效应，因为用相对论进行处理时计算往往变得非常繁琐，而结果与经典情况相差不大。当处理高速运动的物理时，比如高能加速器中的电子，则必须要考虑相对论效应对结果带来的修正。

洛伦兹变换的四维形式

在狭义相对论中，某一事件可以用带有四个参数的时空坐标（t,x,y,z）来描述，洛伦兹变换就是在不同惯性参考系中观察同一事件的时空坐标变换关系，并且是满足四维空间中间隔（s =c t -x -y -z ）不变的变换。如果将x、y、z记成x 、x 、x ，并且令：

那么洛伦兹变换可以写成如下的矩阵形式：

其中

洛伦兹变换的推导

相对原则和光速不变的物理原则是狭义相对论通常的出发点（例：爱因斯坦最初对洛伦兹变换的推导）。实际上洛伦兹变换并不取决于光的物理性质：最重要的是粒子间的作用的地区性：一粒子对另外一粒子的影响作用不能任意快地传递，而作用传递的最高速度必须是所有在所有参照系一样的速度 。此最高速度刚好等于真空中光速。

从群论出发的推导

所有参照系间转换以转换叠加作为乘法组成一个群。它们符合以下公理：

闭合：两个参照系转换叠加得另外一转换。以 [ K → → --> K ′ ′ --> ] {\displaystyle [K\to K^{\prime }]} 写 K {\displaystyle K} 到 K ′ ′ --> {\displaystyle K^{\prime }} 。那对任意三个参照系 [ K → → --> K ′ ′ --> ′ ′ --> ] = [ K → → --> K ′ ′ --> ] [ K ′ ′ --> → → --> K ′ ′ --> ′ ′ --> ] {\displaystyle [K\to K^{\prime \prime }]=[K\to K^{\prime }][K^{\prime }\to K^{\prime \prime }]}

组合律： [ K → → --> K ′ ′ --> ] ( [ K ′ ′ --> → → --> K ′ ′ --> ′ ′ --> ] [ K ′ ′ --> ′ ′ --> → → --> K ′ ′ --> ′ ′ --> ′ ′ --> ] ) = ( [ K → → --> K ′ ′ --> ] [ K ′ ′ --> → → --> K ′ ′ --> ′ ′ --> ] ) [ K ′ ′ --> ′ ′ --> → → --> K ′ ′ --> ′ ′ --> ′ ′ --> ] {\displaystyle [K\to K^{\prime }]\left([K^{\prime }\to K^{\prime \prime }][K^{\prime \prime }\to K^{\prime \prime \prime }]\right)=\left([K\to K^{\prime }][K^{\prime }\to K^{\prime \prime }]\right)[K^{\prime \prime }\to K^{\prime \prime \prime }]}

单位元：存在保留参照系的单位转换 [ K → → --> K ] {\displaystyle [K\to K]}

逆元：对任何参照系转换 [ K → → --> K ′ ′ --> ] {\displaystyle [K\to K^{\prime }]} 都有返回原本参照系的转换 [ K ′ ′ --> → → --> K ] {\displaystyle [K^{\prime }\to K]}

符合群公理的转换矩阵

考虑两个参照系 K {\displaystyle K} 和 K ′ ′ --> {\displaystyle K^{\prime }} ， K ′ ′ --> {\displaystyle K^{\prime }} 的原点相对 K {\displaystyle K} 原点速度为 v {\displaystyle v} （设运动方向为 z {\displaystyle z} 方向，以下忽略无关的 x {\displaystyle x} 和 y {\displaystyle y} 方向）。出于时空的均匀性洛伦兹变换必须保留惯性运动，因此它必须是一个线性转换而可以以矩阵表示：

以上 Λ Λ --> i j {\displaystyle \Lambda _{ij}} 是有待计算的矩阵元。它们是相对速度 v {\displaystyle v} 的函数。

参照系 K ′ ′ --> {\displaystyle K^{\prime }} 的原点 O ′ ′ --> {\displaystyle O^{\prime }} 在参照系 K {\displaystyle K} 的运动：

得

同样参照系 K {\displaystyle K} 的原点 O {\displaystyle O} 在参照系 K ′ ′ --> {\displaystyle K^{\prime }} 的运动：

得

因此主斜两项相等且可称为 γ γ --> ≡ ≡ --> Λ Λ --> 11 = Λ Λ --> 22 {\displaystyle \gamma \equiv \Lambda _{11}=\Lambda _{22}\,} 。还有 Λ Λ --> 21 = − − --> v γ γ --> {\displaystyle \Lambda _{21}=-v\,\gamma } ：

因为 t ′ ′ --> = γ γ --> t {\displaystyle t^{\prime }=\gamma t} ， γ γ --> {\displaystyle \gamma时间膨胀的意义就是时间膨胀的因子。因为时空的各向同性， γ γ --> {\displaystyle \gamma } 只能取决于速度而不取决于方向。也就是说 γ γ --> ( − − --> v ) = γ γ --> ( v ) {\displaystyle \gamma (-v)=\gamma (v)} 。 群元可逆因此取逆矩阵：

当然逆转换只等同于反方向同速的转换。运用上段 γ γ --> {\displaystyle \gamma } 的性质

每项比较得到：

从群的闭合性要求连续两次转换等于以速度和的单次转换。也就是说两个矩阵的积：

必须拥有同样的矩阵型式。这意味着主斜线上两项相等。因此以下比例：

必须是一个和参照系相对速度 v {\displaystyle v} 无关的常数。 插入较前等式得 γ γ --> {\displaystyle \gamma } 的定义：

而最广泛的洛伦兹变换矩阵型式为：

到这里 c 2 = 1 | κ κ --> | {\displaystyle c^{2}={\frac {1}{|\kappa |}}} 就是转换的不变速度。如果 κ κ --> > 0 {\displaystyle \kappa \,>0} ，c是一个速度的下限。这明显与物理现实不符。因此 κ κ --> ≤ ≤ --> 0 {\displaystyle \kappa \leq 0} 。但还可以分成 κ κ --> = 0 {\displaystyle \kappa \,=0} 和 κ κ --> < 0 {\displaystyle \kappa \,<0} 两种情形：

伽利略转换

κ κ --> = 0 {\displaystyle \kappa =0} 得伽利略转换矩阵：

在此情况下时间是绝对的： t ′ ′ --> = t {\displaystyle t^{\prime }=t} 。

洛伦兹变换

在更一般 c = 1 − − --> κ κ --> {\displaystyle c={\frac {1}{\sqrt {-\kappa }}} 的情况就得到先前的洛伦兹变换矩阵：

c {\displaystyle c} 是在所有参照系内不变的速度上限。

到底世界是属于 κ κ --> = 0 {\displaystyle \kappa =0} 还是 κ κ --> < 0 {\displaystyle \kappa <0} 类型是最终只能靠实验验证。例如迈克耳孙-莫雷实验。

洛伦兹变换的推论

由洛伦兹变换可以得到相对论的速度变换公式。设u x 、u y 、u z 分别是物体在惯性坐标系Σ下沿各坐标轴的速度分量，u" x 、u" y 、u" z 分别是物体在惯性坐标系Σ"下沿各坐标轴的速度分量，那么：

如果把v变成-v，u x 、u y 、u z 分别与u" x 、u" y 、u" z 互换，就得到上述速度变换的反变换式。

当速度v远小于光速时，上述速度变换式退化为经典的速度变换式：

洛伦兹变换的几何理解

在平面几何，一个矢量在某座标系统为 ( x , y ) {\displaystyle (x,y)} 。如果我们在原点以 θ θ --> {\displaystyle \theta } 顺时针旋转原本座标轴做新的座标系统。在新系统内，同一矢量座标为: ( x ′ ′ --> , y ′ ′ --> ) {\displaystyle (x^{\prime },y^{\prime })} ：

当然虽然矢量的座标在不同座标系统里面不一样，它的长度不变： ( x ′ ′ --> ) 2 + ( y ′ ′ --> ) 2 = ( x ) 2 + ( y ) 2 {\displaystyle (x^{\prime })^{2}+(y^{\prime })^{2}=(x)^{2}+(y)^{2}} 。 另外如果我们以另外角度 ϕ ϕ --> {\displaystyle \phi } 再旋转一次，那矢量新座标和原座标关系为：

即： 连续的转角可加 。

我们可以相似般把洛伦兹变换看成一种类似的座标旋转。定义快度 w = arctanh β β --> {\displaystyle w={\text{arctanh}}\beta } 。那以上洛伦兹变换公式可以写成（略去不受影响的 x 2 {\displaystyle x^{2}} 和 x 3 {\displaystyle x^{3}} ）：

也就是说： 洛伦兹变换数学上等同于双曲角旋转 。此座标“旋转”中类似“长度”的不变量是：

如果我们先转换到相对原本叁考系统速度为 β β --> 21 {\displaystyle \beta _{21}} 的叁考系统，然后再转换到相对第二个叁考系统速度为 β β --> 32 {\displaystyle \beta _{32}} 的叁考系统。令 w 21 = arctanh β β --> 21 {\displaystyle w_{21}={\text{arctanh}}\beta _{21}} 、 w 32 = arctanh β β --> 32 {\displaystyle w_{32}={\text{arctanh}}\beta _{32}} 。那么在原本叁考系统座标为 ( x 0 , x 1 ) {\displaystyle (x^{0},x^{1})} 的事件在两次转换后叁考系统内座标 ( x ′ ′ --> ′ ′ --> 0 , x ′ ′ --> ′ ′ --> 1 ) {\displaystyle (x^{\prime \prime }{}^{0},x^{\prime \prime }{}^{1})} 为：

所以我们发现洛伦兹变换里直接相加的数量不是速度 β β --> {\displaystyle \beta } 而是这个类似角度的 w = arctanh β β --> {\displaystyle w={\text{arctanh}}\beta } 。日常经验我们使用的伽利略变换把速度直接相加减。这是因为在速度远小于光速（ β β --> ≪ ≪ --> 1 {\displaystyle \beta \ll 1} ）的时候 w {\displaystyle w} 近似速度 w ≃ ≃ --> β β --> {\displaystyle w\simeq \beta } 。

当然我们也可以直接从原本的叁考系统直接转换到最后的叁考系统。如果两者速度为 β β --> 31 {\displaystyle \beta _{31}} ，那么

因此得到相对论速率加法公式。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。