量子退相干
理论概述
开放系统
在经典物理里,孤立系统是一个很有用的概念。理想的孤立系统完全与外在环境相互隔绝,不会与外在环境耦合,不会与外在环境相互传输物质或能量,这样,可以专注研究孤立系统,而不必顾虑到外在环境因素。例如,思考一个移动于空间的圆球,为了简单化分析其感受到地心引力而呈现的运动轨道,可以忽略空气阻力、微风、月亮引力或太阳引力的影响,将这圆球与地球所形成的系统视为一个孤立系统。
与孤立系统迥然不同,开放系统可以与外在环境耦合,可以与外在环境交换物质或能量。近几十年来,物理学者逐渐发觉,当量子系统与外在环境耦合时,会产生量子纠缠,连带地将量子系统内部的量子相干性逐渐泄露至外在环境,因此,开放系统成为促成量子退相干的重要概念。
冯诺伊曼量子测量纲要
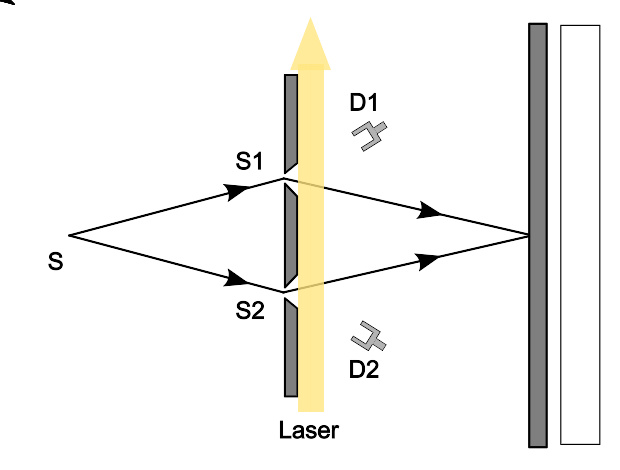
双缝路径实验示意图。从电子源 S {\displaystyle \mathrm {S} } 发射出来的相干电子束,照射在一块刻有两条狭缝 S 1 {\displaystyle \mathrm {S1} } 和 S 2 {\displaystyle \mathrm {S2} } 的不透明挡板。在挡板后方有探测屏。电子抵达探测屏的辐照度会呈黑白相间的条纹,这是电子的干涉图样,展示于示意图最右边。现在,在挡版后面用激光照射,如果激光的光子被电子散射,然后被光子探测器吸收,则可大致知道电子到底是经过哪条狭缝,因为经过狭缝 S 1 {\displaystyle \mathrm {S1} } 的电子通常会使得光子被探测器 D 1 {\displaystyle \mathrm {D1} } 吸收,而经过狭缝 S 2 {\displaystyle \mathrm {S2} } 的电子通常会使得光子被探测器 D 2 {\displaystyle \mathrm {D2} } 吸收。由于电子会被光子搅扰,因此改变轨道,所以原本的干涉图样会变得较为模糊,甚至完全消失,其变化状况依电子路径的分辨程度而定,而分辨程度与激光的辐照度有关。
假设在一个开放量子系统里,有两个正交的态矢量 | ψ ψ --> 1 ⟩ ⟩ --> {\displaystyle |\psi _{1}\rangle } 、 | ψ ψ --> 2 ⟩ ⟩ --> {\displaystyle |\psi _{2}\rangle } ,它们共同形成标准正交基 { | ψ ψ --> i ⟩ ⟩ --> , i = 1 , 2 } {\displaystyle \{|\psi _{i}\rangle ,\ i=1,2\}} ,例如,在双缝路径实验里,如右图所示,它们分别代表粒子移动于两条通过不同狭缝 S 1 {\displaystyle \mathrm {S1} } 、 S 2 {\displaystyle \mathrm {S2} } 的路径量子态。按照 冯诺伊曼量子测量纲要 ( 英语 : Von Neumann measurement scheme ) ,它们与环境态的共同演化式表示为(在这里,环境所扮演的角色就好似激光照射器)
其中, | E i ⟩ ⟩ --> {\displaystyle |E_{i}\rangle } 是初始的环境态, | E 1 ⟩ ⟩ --> {\displaystyle |E_{1}\rangle } 、 | E 2 ⟩ ⟩ --> {\displaystyle |E_{2}\rangle } 是演化后的环境态。
假若系统为 | ψ ψ --> 1 ⟩ ⟩ --> {\displaystyle |\psi _{1}\rangle } ,则环境会演化为 | E 1 ⟩ ⟩ --> {\displaystyle |E_{1}\rangle } ,在双缝路径实验里,光子被探测器 D 1 {\displaystyle \mathrm {D1} } 吸收;假若系统为 | ψ ψ --> 2 ⟩ ⟩ --> {\displaystyle |\psi _{2}\rangle } ,则环境会演化为 | E 2 ⟩ ⟩ --> {\displaystyle |E_{2}\rangle } ,在双缝路径实验里,光子被探测器 D 2 {\displaystyle \mathrm {D2} } 吸收。
注意到量子态 | ψ ψ --> 1 ⟩ ⟩ --> {\displaystyle |\psi _{1}\rangle } 、 | ψ ψ --> 2 ⟩ ⟩ --> {\displaystyle |\psi _{2}\rangle } 不会因为开放系统与环境相互作用而改变,因此,环境可以被想像为正在进行一种理想测量,称为 量子非破坏性测量 ( 英语 : quantum nondemolition measurement ) 。
假设量子系统的初始态为叠加态
其中, c 1 {\displaystyle c_{1}} 、 c 2 {\displaystyle c_{2}} 分别为量子系统处于 | ψ ψ --> 1 ⟩ ⟩ --> {\displaystyle |\psi _{1}\rangle } 、 | ψ ψ --> 2 ⟩ ⟩ --> {\displaystyle |\psi _{2}\rangle } 的概率幅,遵守归一条件 | c 1 | 2 + | c 2 | 2 = 1 {\displaystyle |c_{1}|^{2}+|c_{2}|^{2}=1} 。
这量子系统的相干性与复数 c 1 {\displaystyle c_{1}} 、 c 2 {\displaystyle c_{2}} 的相对相位密切关联。量子退相干的目的就是在消灭这相对相位所导致的相干性。
遵守冯诺伊曼量子测量纲要,随着时间流易, | ψ ψ --> i ⟩ ⟩ --> {\displaystyle |\psi _{i}\rangle } 与环境态 | E i ⟩ ⟩ --> {\displaystyle |E_{i}\rangle } 会演化为
其中, | Ψ Ψ --> i ⟩ ⟩ --> {\displaystyle |\Psi _{i}\rangle } 、 | Ψ Ψ --> f ⟩ ⟩ --> {\displaystyle |\Psi _{f}\rangle } 分别为整体系统的初始态与终止态。
约化密度算符
假设对整个系统的可观察量 O {\displaystyle O} 做测量,而此可观察量 O {\displaystyle O} 只涉及到量子系统,未涉及到环境:
其中, O ^ ^ --> {\displaystyle {\hat {O}}} 是对应于可观察量 O {\displaystyle O} 的算符, O ^ ^ --> s {\displaystyle {\hat {O}}_{s}} 是其涉及到量子系统的部分, I ^ ^ --> e {\displaystyle {\hat {I}}_{e}} 是在环境的单位算符。
则可观察量 O {\displaystyle O} 期望值,是取其算符与密度算符的乘积对于整个系统的迹数。这迹数也是取其作用于量子系统的算符与约化密度算符两者的乘积对于量子系统的迹数:
其中, ρ ρ --> ^ ^ --> {\displaystyle {\hat {\rho }}} 是整个系统的密度算符, ρ ρ --> ^ ^ --> s {\displaystyle {\hat {\rho }}_{s}} 是量子系统的约化密度算符。
因此,量子系统的性质只与其约化密度算符有关。如果知道量子系统的约化密度算符,则可计算量子系统的任意可观察量的期望值,从而分析量子系统的性质。约化密度算符 ρ ρ --> s {\displaystyle \rho _{s}} 定义为取整个系统对于环境的迹数:
经过一番运算,可以得到
分辨性
假设 ⟨ ⟨ --> E 2 | E 1 ⟩ ⟩ --> = 1 {\displaystyle \langle E_{2}|E_{1}\rangle =1} ,即 | E 1 ⟩ ⟩ --> {\displaystyle |E_{1}\rangle } 就是 | E 2 ⟩ ⟩ --> {\displaystyle |E_{2}\rangle } ,两个环境态完全重叠,则整个系统的量子态可以写为两个纯态的张量积:
这意味着量子系统与环境彼此之间不存在量子纠缠。对于环境做测量,无法从测量结果推断量子系统是处于量子态 | ψ ψ --> 1 ⟩ ⟩ --> {\displaystyle |\psi _{1}\rangle } 或 | ψ ψ --> 2 ⟩ ⟩ --> {\displaystyle |\psi _{2}\rangle } 。量子系统的相干性仍旧停留在量子系统里,没有退定域至整个系统。在双缝路径实验里,这表示激光的光子与电子碰撞后被散射至同样的探测器,这可能是因为电子在两条路径的运动很类似。
假若 ⟨ ⟨ --> E 2 | E 1 ⟩ ⟩ --> {\displaystyle \langle E_{2}|E_{1}\rangle } 越小,则 | E 1 ⟩ ⟩ --> {\displaystyle |E_{1}\rangle } 、 | E 2 ⟩ ⟩ --> {\displaystyle |E_{2}\rangle } 的重叠部分越小。取 ⟨ ⟨ --> E 2 | E 1 ⟩ ⟩ --> = 0 {\displaystyle \langle E_{2}|E_{1}\rangle =0} 的极限,即 | E 1 ⟩ ⟩ --> {\displaystyle |E_{1}\rangle } 、 | E 2 ⟩ ⟩ --> {\displaystyle |E_{2}\rangle } 不相互重叠。假若得知环境态是 | E 1 ⟩ ⟩ --> {\displaystyle |E_{1}\rangle } ,则系统量子态就是 | ψ ψ --> 1 ⟩ ⟩ --> {\displaystyle |\psi _{1}\rangle } ,假若得知环境态是 | E 2 ⟩ ⟩ --> {\displaystyle |E_{2}\rangle } ,则系统量子态就是 | ψ ψ --> 2 ⟩ ⟩ --> {\displaystyle |\psi _{2}\rangle } 。因此,从经典的宏观环境态可以分辨开放系统的微观量子态是 | ψ ψ --> 1 ⟩ ⟩ --> {\displaystyle |\psi _{1}\rangle } 或 | ψ ψ --> 2 ⟩ ⟩ --> {\displaystyle |\psi _{2}\rangle } 。在双缝路径实验里,这表示激光的光子被电子散射后的结果大不相同,这可能是因为电子在两条路径的运动很容易被分辨出来。
虽然对于每一个案例,并不一定 ⟨ ⟨ --> E 2 | E 1 ⟩ ⟩ --> {\displaystyle \langle E_{2}|E_{1}\rangle } 必须趋于零,但很多关于量子系统与环境相互作用的物理实际模型都会显示出这种极限,因为环境拥有几乎无穷大的自由度,在双缝路径实验里,激光的光子会不断的与电子发生碰撞,从而分辨出电子的运动路径,所以, ⟨ ⟨ --> E 2 | E 1 ⟩ ⟩ --> {\displaystyle \langle E_{2}|E_{1}\rangle } 趋于零是很合理的设定。
退相干机制
回想约化密度算符为
在双缝路径实验里,从约化密度算符,可以计算出在探测屏位置为 x {\displaystyle x} 的电子密度 D ( x ) {\displaystyle D(x)} :
注意到最后一个实值项就是干涉项。当设定 ⟨ ⟨ --> E 2 | E 1 ⟩ ⟩ --> {\displaystyle \langle E_{2}|E_{1}\rangle } 趋于零时,这干涉项也会趋于零,因此,干涉图案会消失无信息相位相干信息也不见踪影,电子密度 D ( x ) {\displaystyle D(x)} 变为
这就是量子退相干的效应。量子退相干不是一种量子力学诠释,而是利用量子力学分析开放量子系统与环境相互作用所得到的结果。它严格遵守量子力学,并没有对量子力学的基础表述做任何修改。
由于设定 ⟨ ⟨ --> E 1 | E 2 ⟩ ⟩ --> {\displaystyle \langle E_{1}|E_{2}\rangle } 趋于零,约化密度算符被对角化:
这意味着,相位相干信息已不再存在于量子系统层次,相位相干信息已泄漏至外在环境,只有从观测整个系统,才能重新获得相位相干信息。
只单独考虑量子系统,其随着时间流易的演化是呈非幺正性,虽然量子系统与环境整体随着时间流易的演化是呈幺正性。 这样,量子系统的演化貌似具有不可逆性。由于环境拥有几乎无穷大的自由度,而且很难适当地操纵环境,因此,一般而言,量子退相干具有不可逆性。
尽管对应于约化密度算符的矩阵(称为约化密度矩阵)与描述混合态的密度矩阵在形式上完全相同,无法从矩阵区分出到底是纠缠系统的一部分还是混合态,约化密度算符所描述的不是“真混合物”(proper mixture)。而是一种“瑕混合物”(improper mixture) 。对于双缝路径案例,假设量子系统处于混合态 | c 1 | 2 | ψ ψ --> 1 ⟩ ⟩ --> ⟨ ⟨ --> ψ ψ --> 1 | + | c 2 | 2 | ψ ψ --> 2 ⟩ ⟩ --> ⟨ ⟨ --> ψ ψ --> 2 | {\displaystyle |c_{1}|^{2}|\psi _{1}\rangle \langle \psi _{1}|+|c_{2}|^{2}|\psi _{2}\rangle \langle \psi _{2}|} ,即处于量子态 | ψ ψ --> 1 ⟩ ⟩ --> {\displaystyle |\psi _{1}\rangle } 、 | ψ ψ --> 2 ⟩ ⟩ --> {\displaystyle |\psi _{2}\rangle } 的概率分别为 | c 1 | 2 {\displaystyle |c_{1}|^{2}} 、 | c 2 | 2 {\displaystyle |c_{2}|^{2}} ,或者假设量子系统与环境处于纠缠态 | ψ ψ --> f ⟩ ⟩ --> = c 1 | ψ ψ --> 1 ⟩ ⟩ --> | E 1 ⟩ ⟩ --> + c 2 | ψ ψ --> 2 ⟩ ⟩ --> | E 2 ⟩ ⟩ --> {\displaystyle |\psi _{f}\rangle =c_{1}|\psi _{1}\rangle |E_{1}\rangle +c_{2}|\psi _{2}\rangle |E_{2}\rangle } ,只测量量子系统,并无法区分出这量子系统的物理状态。
退相干时间尺度
对于宏观物体而言,由于外在环境会有很多微观物体会与之相互作用,量子退相干是非常快速的过程,说明为什么无法观察到量子干涉行为。约化密度矩阵的对角元素有效消失所需的时间称为退相干时间。对于日常发生的宏观过程,退相干时间非常短暂。 特别而言,在物理学者给出的很多不同的退相干模型里,不同的环境态 | E i ( t ) ⟩ ⟩ --> {\displaystyle |E_{i}(t)\rangle } 、 | E j ( t ) ⟩ ⟩ --> {\displaystyle |E_{j}(t)\rangle } 通常遵守指数衰变:
其中, t {\displaystyle t} 是时间, τ τ --> d {\displaystyle \tau _{d}} 是退相干时间尺度。

处于位置叠加态的物体(以黄绿色表示)与环境粒子相互碰撞,由于量子纠缠,物体的相干性质会被泄漏至环境。
每一种退相干模型都有其特征的退相干时间尺度。例如,在空间退相干模型里,像空气分子或光子一类的环境粒子,因为与处于不同位置叠加态的物体发生碰撞,而促成量子退相干,其环境态 | E x ( t ) ⟩ ⟩ --> {\displaystyle |E_{x}(t)\rangle } 、 | E y ( t ) ⟩ ⟩ --> {\displaystyle |E_{y}(t)\rangle } 的指数衰变的形式为
其中, x {\displaystyle x} 、 y {\displaystyle y} 分别为物体质心的位置, Λ Λ --> {\displaystyle \Lambda } 是散射常数。
对于处于位置叠加态的物体,退相干时间尺度 τ τ --> Δ Δ --> {\displaystyle \tau _{\Delta }} 与质心距离 Δ Δ --> = | x − − --> y | {\displaystyle \Delta =|x-y|} 成平方反比:
假若 x {\displaystyle x} 、 y {\displaystyle y} 的质心距离越近,则环境粒子被位于这两个位置的物体散射后的量子态越相似,即两个对应的环境态的重叠部分越大,因此越困难分辨物体的位置,需要越多环境粒子来做分辨,所以退相干时间尺度越悠久;反过来说,假若 x {\displaystyle x} 、 y {\displaystyle y} 的质心距离越远,越容易分辨物体在哪个位置,因此只需要几个环境粒子就可以完成分辨,所以退相干时间尺度越短暂。当质心距离足够遥远,单独散射就能够解析物体的位置之时,退相干时间尺度会变得与质心距离无关,是总散射率的倒数:
假设在空间里的物体,因为遭到外在环境里的热力学光子散射,而出现量子退相干,则其散射常数 Λ Λ --> {\displaystyle \Lambda } 通过理论分析以方程表示为
其中, a {\displaystyle a} 是物体尺寸(单位为cm), T {\displaystyle T} 是绝对温度(单位为K)
假设是遭到空气分子散射,则其散射常数 Λ Λ --> {\displaystyle \Lambda } 在正常气压为
由此两个方程可知,散射常数与物体尺寸、绝对温度有不同程度的相关。
以下列出在不同环境下,对于不同尺寸的物体,且量子干涉距离等于物体尺寸( Δ Δ --> = a {\displaystyle \Delta =a} ),退相干时间尺度 τ τ --> d {\displaystyle \tau _{d}} 的估算数值(单位为秒):
实验观察
量子退相干通常发生的很快,因此很难制成处于宏观或介观的叠加态物体。为了要实验验证量子退相干的效应、见证量子与经典之间的平滑边界、检验与改良描述量子退相干的理论模型、找出任何不同于量子力学ㄠ正演化行为之处,必须完成以下几件极具挑战性的任务:
制备出可分辨的几个宏观态或介观态的量子叠加态。
设计一套证实量子叠加的方法。
量子退相干时间尺度必须足够长久,这样才能正确地观测量子退相干。
设计一套监督量子退相干的方法。
腔量子电动力学实验
1996年,在法国巴黎高等师范学校,物理学者塞尔日·阿罗什实验团队在腔量子电动力学实验中,首先定量观测到辐射场的介观叠加态的相位相干性逐渐地因量子退相干而被摧毁。
在这实验里,单独里德伯铷原子被传输通过含有辐射场的 微波腔 ( 英语 : microwave cavity ) ,而这里德伯原子是处于两个量子态所组成的叠加态,其中一个量子态会使得辐射场发生相移,因此促使辐射场从原先所处的非叠加态变为叠加态。由于光子散射于腔镜子的瑕疵,辐射场会逐渐失去其相位相干性给环境。传送第二个里德伯原子通过微波腔,可以测量出辐射场的相位相干性。从分析在不同延迟时间下相位相干性的数据,可以实验证实量子退相干效应。
因为研究能够量度和操控个体量子系统的突破性实验方法,阿罗什荣获2012年诺贝尔物理学奖。
量子干涉学实验
2002年,奥地利维也纳大学物理学者安东·蔡林格研究团队发表论文报告观察C 70 富勒烯干涉行为的结果。C 70 富勒烯的质量为840amu,直径约为1nm,是由超过1000个微观粒子所组成的相当复杂的物体,因此很不容易观察到量子干涉效应,必须特别使用一种应用 塔尔博特效应 ( 英语 : Talbot effect ) 的干涉仪,称为 塔尔博特-劳澳干涉仪 ( 英语 : Talbot-Lau interferometer ) 。碰撞退相干、热力学退相干、振动摄动引起的退相位 ,这几种效应会促使干涉图案的可视性会逐渐衰减。量子退相干可以用可视性的衰减来量度,因此可视性的衰减表征量子退相干效应。
量子退相干与量子信息科学
退相干现象对量子信息科学的影响可大致分成两大内容来说明:量子计算与量子通信。我们知道在量子信息科学中,量子系统的状态含藏着信息的意义。量子退相干会使我们所在意的系统出现信息部分或完全丧失的结果,因此在量子计算上会造成计算结果出现误差干扰;而在量子通信上,一个环境充满扰动的信息传递通道(channel),在通道末端的收受者则有收到噪声及错误讯息的可能,需要除错系统如编码方法之协助。
历史
1935年,在普林斯顿高等研究院,阿尔伯特·爱因斯坦、博士后纳森·罗森、研究员鲍里斯·波多尔斯基合作完成论文《物理实在的量子力学描述能否被认为是完备的?》,并且将这篇论文发表于5月份的《物理评论》 。这是最早探讨量子纠缠的一篇论文。在这篇论文里,他们详细表述爱因斯坦-波多尔斯基-罗森佯谬,试图借着一个思想实验来论述量子力学的不完备性质 。他们并没有更进一步研究量子纠缠的特性。
薛定谔仔细阅读了爱因斯坦研究团队的论文。稍后不久,他发表了一篇论文,对于“量子纠缠”这术语给予定义,并且研究探索相关概念。薛定谔体会到这概念的重要性,他表明,量子纠缠不只是量子力学的某个很有意思的性质,而是量子力学的特征性质;量子纠缠在量子力学与经典思路之间做了一个完全切割 。为了进一步显示量子力学的不完备性,薛定谔将量子力学应用到宏观效应中,从而构思了著名的薛定谔猫思想实验。这思想实验明显地呈现出量子至经典变迁的问题。
在之后40年,量子至经典变迁的问题并未得到解答,主要有两个原因,一是由于物理学者认为这论题不常出现于宏观世界,并且没有什么实际用途,二是由于物理学者并未发现环境会扮演那么关键的角色促成了量子至经典变迁 1970年,德国物理学者 汉斯·泽贺 ( 英语 : Heinz Zeh ) 发表了首篇关于量子退相干的论文,他强调,所有宏观系统都是开放系统,都会强烈地与环境相互作用.它们不会遵守薛定谔方程,因为,薛定谔方程只适用于孤立系统 。这崭新的量子退相干概念并没有立刻吸引到学术界的注意。1981至1982年之间,波兰物理学者 沃杰克·祖瑞克 ( 英语 : Wojciech Zurek ) 在《物理评论D》发表了两篇关键性论文,他指出经典系统自然而然地将内含的量子相干性泄漏至环境,因而导致量子退相干的后果,在处理波函数坍缩问题时,不能够忽略这后果。祖瑞克的两篇论文使得量子退相干成为热门量子论题 。1984年,祖瑞克推导出估算量子退相干时间尺度的公式,可以很容易地对于一般量子系统进行相关估算 。隔年,泽贺与学生 艾瑞曲·犹斯 ( 英语 : Erich Joos ) 共同给出一个模型,能够详细地描述因环境粒子散射而产生量子退相干后果的全部过程。1991年,祖瑞克在《 今日物理 ( 英语 : Physics Today ) 》发表了一篇论文,将量子退相干介绍给更广泛学术界,从而引起更多物理学者注意到这学术领域的发展 。
注释
^ 碰撞退相干指的是C 70 富勒烯与环境气体分子之间的碰撞而发生的量子退相干。热力学退相干指的是C 70 富勒烯因发射热力学辐射而发生的量子退相干。干涉仪的衍射光栅会振动,因此造成经典的振动摄动。
延伸阅读
Mario Castagnino, Sebastian Fortin, Roberto Laura and Olimpia Lombardi, A general theoretical framework for decoherence in open and closed systems , Classical and Quantum Gravity, 25, pp. 154002–154013, (2008).
参见
相干性
环境诱导超选择
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。

- 有价值
- 一般般
- 没价值








24小时热门
推荐阅读



知识互答
关于我们

APP下载



























{{item.time}} {{item.replyListShow ? '收起' : '展开'}}评论 {{curReplyId == item.id ? '取消回复' : '回复'}}