简介

即使存在力，也可能没有作功。例如，在匀速圆周运动中，向心力没有作功，因为做圆周运动的物体的动能没有发生变化。同样的，桌上的一本书，尽管桌对书有支持力，但因没有位移而没有作功。

单位

国际单位制的单位为焦耳（J）。焦耳被定义为用1牛顿的力对一物体使其发生1米的位移所做的机械功的大小。量纲相同的单位牛·米有时也使用，但是一般牛·米用于力矩，使其跟功和能区别开。

非国际单位制单位包括尔格、英尺·磅、千瓦时（kW•h）、大气压力、马力时（HP•h）。而由于具有相同的物理量─热能，偶尔会见到以热量热能形式表示的测量单位，如：卡路里（cal）、BTU等。

功与能

功与能息息相关，根据系统能量的守恒，内部总能量的变化等于添加的热能加上环境对系统所作的功。见热力学第一定律。

d E = δ δ --> Q + δ δ --> W {\displaystyle \mathrm {d} E=\delta Q+\delta W}

功能原理

1.保守力作功使“存”在物体中的位能释放出来，亦即 保守力作功等于负的位能变 ：

W = − − --> Δ Δ --> U {\displaystyle W=-\Delta U}

2.非保守力作功时，若有保守力作负功则优先化为位能，剩下的功才化为物体的动能，即 非保守力作功等于总力学能（动能+位能）变 ：

W = Δ Δ --> E = Δ Δ --> E k + Δ Δ --> U {\displaystyle W=\Delta E=\Delta E_{\rm {k}}+\Delta U}

3.综合以上两点，一物体所受的合力包含了保守力与非保守力，非保守力使总力学能变，而保守力将之部分化为位能，二者相加，即 合力作功等于动能变 ：

W = Δ Δ --> E k {\displaystyle W=\Delta E_{\rm {k}}}

根据这些公式证明功是与作用力相关的能量，所以作功是能被测量的，是一种具有物理单位的能量。这理所讨论的作功、能量原理与电器和能源的作功原理是相同的。

约束力

约束力决定了系统中物件的位移，将其限制在范围内（以斜面加重力为例，当物体受到无法再伸长的紧绳约束使其不能再下滑，物体就会 卡 在斜面上）。它消除了在该方向上所有的位移，即物体平行此力的速度被约束为0，因此 约束力不对系统作功 。

例如：用一根绳子系上一个小球做匀速圆周运动，小球会受到来自绳子，方向指向圆心的一个向心力。这个力的方向和球速度的方向垂直，所以这个力不作功（W=0）。又如桌上有一本书，施加外力会使书在桌面上移动。如果再对书施加一个垂直的力（实际上书受到的重力和支持力就属于这个力），和其欲移动之方向垂直，则此约束力（施加的垂直力）不作功。

磁场中的带电粒子受到磁力（洛伦兹力）的大小为F = q v×B ，其中q为电荷，v是粒子速度，而B为磁场强度。外积结果恒垂直于两原向量，因此F⊥v。而两垂直向量的内积恒零，因此磁力作的功W = F · v = 0。磁力可改变此粒子运动的方向，但是永远无法改变运动速度（也就是动能）。

数学计算

对于一移动的物体而言，作功量/时间可以从距离/时间（即速度V）来计算。因此，在任何时刻，力所作的功率（焦耳/秒、瓦），其值为力的标量积（矢量）和作用点上的速度矢量。力的标量积和速度被归类为瞬时功率。

而正如速度可能会随着时间的推移以获得更长的距离，同一条路径上的总功率也同样是作用点沿着同一条路径上之瞬时功率的时间积分的总和。

功是指质点受外力作用位移而产生的量，当质点移动时，它沿着曲线 X 和速度 V 在所有的时间 t 。少量的功 δW 发生在瞬时时间 δt 能够写成：

其中 C 的位移是从 x （t 1 ）到 x （t 2 ），计算质点位移的积分。

如果力的方向总是沿着这条线，力的大小为 F ，那么此积分可简化为：

其中 s 是沿着直线的位移，假设 F 固定，且沿着此直线，则此积分可进一步简化成：

其中 d 是质点沿着直线前进的距离。

此计算可归纳为恒定力并非延著线而是沿着质点。在此情况下点的乘积 F ·d x = F cos θ dx，其中 θ 是力矢量和运动方向之间的角度。即：

一般常见的情况，施加的力和速度矢量对身体成90 角（中央力朝体绕一圆圈运动），由于cos90 为0，所以不作功。因此可以延伸至重力对于星球在圆形轨道上运动不作功（此为理想情况，一般情况下轨道略呈椭圆形）。

此外身体作一等速圆周运动受到机械外力作用时，作的功也为0，就像在一理想情况之无摩擦力的离心机中作等速圆周运动一般。

计算功在时间和力作用在一直线路径上的数值只适用在最简单的情况下，如上文所述。如果力会变化，或身体延曲线方向移动，物体可能转动甚至并非刚性物体，那么其所作的功只和作用力的角度、路径有关，并且只有部分的力平行在作用点上形成的速度才作功 （相同方向为正，反方向为负值），此处的力可以被描述为标量或是切线分量的标量。（Fcosθ，其中θ是力和速度之间的夹角）。

至于功最普遍的定义如下：力作功是其延著作用点上的路径之切线分量的标量也就是线性积分。

转矩和转动

转矩是从相等但方向相反的力作用于刚性体上两个不同的点所形成。这些力总合为零，但它会对物体影响形成转矩 Τ ，计算作功形成的转矩公式为：

如果角速度矢量保持恒定的方向，那么可以写成：

如果转矩 T 与角速度矢量一致，那么可写成：

而且若转矩和角速度是恒定的，那么功可写成这个形式：

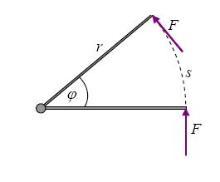
A force of constant magnitude and perpendicular to the lever arm

此结果可以更简单的理解，如图所示。这股力将通过圆弧的距离 s=rφ ，所作的功即是：

以上，请注意只有转矩在角速度矢量方向的部分才有作功。

力与位移

力与位移都是矢量。功是力与位移的内积，为标量。

其中 θ θ --> {\displaystyle \theta } 是力矢量和位移矢量的夹角。

为使此式正确，力须为常矢量，路径须为一条直线。

如力随时间变化或路径不为直线，上式不再适用，此时需使用曲线积分。故功的一般公式为：

其中

表达式 δ δ --> W = F → → --> ⋅ ⋅ --> d s → → --> {\displaystyle \delta W={\vec {F}}\cdot \mathrm {d} {\vec {s}}} 是一个非恰当微分， W C {\displaystyle \textstyle {W_{C}}} 与路径有关，求微分后不能得到 F → → --> ⋅ ⋅ --> d x → → --> {\displaystyle {\vec {F}}\cdot \mathrm {d} {\vec {x}}} 。

非零力可以不作功，这一点与冲量不同。冲量是力对时间的累积。冲量是矢量，所以圆周运动时虽向心力不作功，但产生了对物体的非零冲量。

力矩

力矩所作功可由下式计算得到：

其中 τ τ --> {\displaystyle \tau } 为力矩。

功与动能

功与动能的原理（也可称功与能的原理），意指合力作用在物质上（合力作功）的功等于物质的动能变化量

合力 W 在质点上所作的功等于其动能的变化量 E k {\displaystyle E_{k}} ,

v 1 {\displaystyle v_{1}} and v 2 {\displaystyle v_{2}} 分别是质点的初速度和末速度，m则是质量。

概述

功与能的原理由牛顿第二运动定律推导，其中包括作用在质点上的合力和约束反力对质点造成的位移量。

对于匀变速直线运动的情形，推导如下式。

一般情况下的推导则如下式。

参考

Serway, Raymond A.; Jewett, John W. Physics for Scientists and Engineers 6th ed. Brooks/Cole. 2004. ISBN 0-534-40842-7. 引文格式1维护：冗余文本 (link)

Tipler, Paul. Physics for Scientists and Engineers: Mechanics 3rd ed., extended version. W. H. Freeman. 1991. ISBN 0-87901-432-6.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。