理论内涵

人在不确定条件下的决策选择，取决于结果与展望（预期、设想）的差距而非单单结果本身。即，人在决策时会在心里预设一个参考标准，然后衡量每个决定的结果，与这个参考标准的差别是多大。例如，一个人展望（预期）能得到奖金 500 元，当他的决策让他得到奖金 500 元，他会觉得没什么；若他有办法得到多于预期的 500 元，多数人会审慎地考量这方法（决策）带来的风险，以免失去展望（预期）回报；如果相反，即使他有另一个比较安全，但让他少得100元奖金的办法（决策），那多数人会宁可冒较大风险，以获取展望（预期）回报。

此理论是为改进博弈论中的期望效用假说而建立。它比较符合心理学观察结果，能比较写实地描述一个人，在风险决策（如金融投资）之时的心理。

数学模型

假设一个人衡量决策得失的数学函数（PT 函数）为： U=w(p1)v(x1)+w(p2)v(x2)+… … -->,{\displaystyle U=w(p_{1})v(x_{1})+w(p_{2})v(x_{2})+\dots ,}当中 x1,x2,… … -->{\displaystyle x_{1},x_{2},\dots } 是各个可能结果， p1,p2,… … -->{\displaystyle p_{1},p_{2},\dots } 是这些结果发生的或然率。 v{\displaystyle v} 是所谓“价值函数 (value function)”，表示不同可能结果，在决策者心中的相对价值。根据本理论，价值函数的线，应当会穿过中间的“参考点 (reference point)”，并形成一个如下的 s 型曲线：

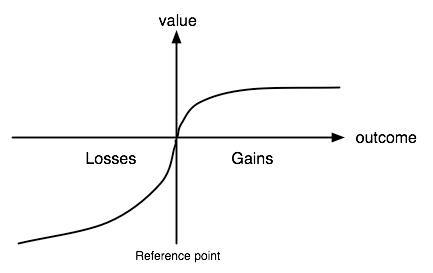
它的不对称性表明，一个损失结果对应价值的绝对值，比获利结果对应价值的绝对值更大，也就是所谓的“损失厌恶性(loss aversion)”。与期望效用假说不同，本理论衡量获利与损失的方法，并不考虑所的“绝对所得 (absolute wealth)”。函式 w{\displaystyle w} 是为“可能性比重函数 (probability weighting function)”，用以表达一般人对概率的反应 —— 一般而言，人对极不可能发生的事，会过度反应 (over-react)，而对中度、高度可能发生的事，会反应迟钝 (under-react)。

举例

假设一个人打算买保险，设投保所保障项目，有 1% 的机会遇险；如果遇险，投保人的损失为 $1,000 ；而保费为 $15。我们引用展望理论前，先要设一个“参考点”，而它可能是 (1) 现有的财富状况，或者 (2) 最坏的情况，即损失$1,000。

若我们用“现有的财富状况”作参考点，投保人可以付保费 $15，则“PT 效用值 (PT utility) ”为 v(− − -->15){\displaystyle v(-15)} ，而他的可能所得 $0 (可能性 99%)，或者 -$1,000 (可能性 1%)。整体 PT 效用值将为：w(0.01)× × -->v(− − -->1000)+w(0.99)× × -->v(0)=w(0.01)× × -->v(− − -->1000){\displaystyle w(0.01)\times v(-1000)+w(0.99)\times v(0)=w(0.01)\times v(-1000)}我们可以根据公式，计算出效用值的数值。若套用一般的函数，由于 v{\displaystyle v} 在损失时员有凸面性 (convexity) ，所以公式的第一项的绝对值会比较大，令整体 PT 效用值得远小于 v(− − -->15){\displaystyle v(-15)}。事故损失，或者说不买保险损失（绝对值），大于买保险损失，而令买保险的PT效用值看起来，较不买负的少。这表示该位投保人会买保险。

第二种情况，若果我们用“损失 $1,000”作为参考点，由于 v{\displaystyle v} 在获利时具有凹面性 (concavity) ，会令 PT 效用值增加，结果大于 v(− − -->15){\displaystyle v(-15)}，致令买保险看起来，比不买更吸引。这表示该位投保人也会买保险。

此理论引申的四个基本结论

确定效应：处于收益状态时，多数人是风险厌恶者。

反射效应：处于损失状态时，多数人是风险喜好者。

损失规避：多数人对损失比对收益敏感。

参照依赖：多数人对得失的判断往往由参照点决定。

简言之，人在面临获利时，不愿冒风险；而在面临损失时，人人都成了冒险家。而损失和获利是相对于参照点而言的，改变评价事物时的参照点，就会改变对风险的态度。

相关条目

决策论

预期效用假说

损失规避

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。