更多文章
更多精彩文章

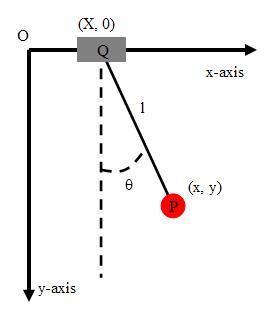
布朗运动为原型
原朗之万方程描述了布朗运动由于流体的分子的碰撞,粒子在流体中做无规则运动,
这里,自由度是粒子的位置x,m表示粒子的质量。作用在粒子上的力写成正比于粒子的速度(斯托克斯定律)的粘滞力,和一个表示流体分子碰撞影响的噪声项 η(t)的和。力η(t)具有高斯概率分布与相关函数
其中kB是波耳兹曼常数和T是温度。该δ函数在时间上的相关性形式表示在时间t上的力,其被假定为在任何其他时间里完全不与它相关。这是一个近似值; 实际的随机力具有对应于分子碰撞时间的非零相关时间。然而,朗之万方程是用来描述在一个更长时间刻度上“宏观”粒子的运动,并在此极限上的δ-相关和朗之万方程变得精确。 朗之万方程的另一个典型特征是随机力的相关函数中衰减系数λ的出现,这一事实也被称为爱因斯坦关系。
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。












{{item.time}} {{item.replyListShow ? '收起' : '展开'}}评论 {{curReplyId == item.id ? '取消回复' : '回复'}}