用词

电磁感应 现象不应与 静电感应 混淆。电磁感应将电动势与通过电路的磁通量联系起来，而静电感应则是使用另一带电荷的物体使物体产生电荷的方法。

麦克斯韦-法拉第方程

本节是一段题外话，作用是区分本条目中的“法拉第定律”及麦克斯韦方程组中用同一个名字的∇×E方程。于本条目中∇×E方程会被称为 麦克斯韦-法拉第方程 。

麦克斯韦于1855年总结出法拉第定律的旋度版本，而亥维赛则于1884年将定律重写成 旋度 方程：

其中

方程的意义是，如果电场的空间依赖在页面上成逆时针方向（经右手定律，得旋度矢量会从页面指出），那么磁场会因时间而更少指出页面，更多地指向页面（跟旋度矢量异号）。方程跟磁场的 变量 有关系。故磁场不一定要指向页面，只需向该方向转动即可。

本方程（在本条目中被称为麦克斯韦-法拉第方程）最著名的地方在于它是麦克斯韦方程组中的四条方程之一。

在麦克斯韦-法拉第方程中，亥维赛用的是 时间偏导数 。不使用麦克斯韦用过的时间全导数，而使用时间偏导数，这样做使得麦克斯韦-法拉第方程不能说明动生电动势。 。然而，麦克斯韦-法拉第方程很多时候会被直接称为“法拉第定律”。

在本条目中“法拉第定律”一词指的是通量方程，而“麦克斯韦-法拉第方程”指的则是亥维赛的 旋度 方程，也就是现在的麦克斯韦方程组中的那一条。

通过表面的磁通量及圈中的电动势

图一：面积分的定义需要把面分成小的面积元。每个元素跟一个矢量d A 联系，该矢量的大小等于面积元的面积，而方向则是跟面积元垂直并向外。

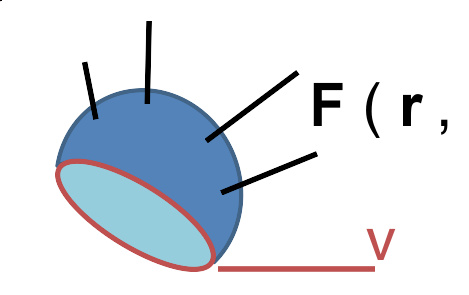
图二：于空间内有定义的一矢量场 F （ r ， t ），及以曲线∂Σ为边界的一表面Σ，在场的积分范围内以速度 v 移动。

法拉第电磁感应定律用到通过一表面 Σ 的磁通量Φ B ，其积分形式定义如下：

其中d A 为移动面 Σ ( t )的面积元， B 为磁场， B ·d A 为矢量点积。见图一。更多细节见面积分及磁通量条目。设该表面有一个开口，边界为闭合曲线 ∂Σ ( t )。见图二。

当通量改变时，把一电荷在闭合曲线中 ∂Σ ( t )移一圈（每单位电荷）所作的功 E {\displaystyle ^{\mathcal {E}}} ，也就是电动势，可由法拉第电磁感应定律求得：

其中：

设有一紧缠线圈，圈数为N，每圈通量皆为Φ B ，法拉第电磁感应定律指出：

在选择路径 ∂Σ ( t )求电动势时，路径须满足两个基本条件：（一）路径闭合；（二）路径必需能描述到电路各部分的相对运动（这就是 ∂Σ ( t )中变量为时间的原因）。路径并 不 一定要跟随电流的流动路线，但用通量定律求出的电动势，理所当然地会是通过所选路径的电动势。假若路径并不跟随电流的话，那么那电动势可能不是驱动着电流的那一电动势。

例一：空间变强磁场

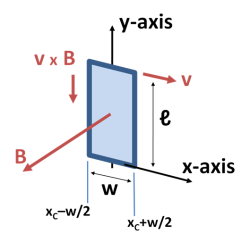
图三：闭合的长方形线圈，以速率 v 沿 x 轴移动，其所处的磁场 B 随 x 的位置而变。

考虑图三的长方形线圈，它在 xy 平面上向 x 方向以速率 v 移动。因此，线圈中心 x C 满足 v = dx C /dt 。线圈在 y 方向的长度为ℓ， x 方向的宽度为 w 。一不随时间改变，而随 x 方向改变的磁场 B(x) 指向 z 方向。左边的磁场为 B ( x C − w/2 )，右边的磁场为 B ( x C + w/2 )。电动势可直接求得，或由上述的法拉第电磁感应定律求得。

洛伦兹力法

在线圈左边的一电荷 q ，所受的洛伦兹力为 q v× B k = − qvB(x C − w/2) j （ j 、 k 分别为y方向及z方向的单位矢量，见矢量积），因此左边整段电线的电动势（单位电荷所作的功）为 vℓB(x C − w/2) 。可用相同的论述，求出右边电线的电动势为 vℓB(x C + w/2) 。两股电动势互相抵抗，将正电荷推向线圈底部。由于这时磁场的强度会向x方向增强，所以右边的力最强，电流会顺时针流动：使用右手定则，电流所产生的磁场会抵抗外加的磁场。 驱动电流的电动势必须向逆时针方向增加（抵抗电流）。把电动势向逆时针方向加起来得：

法拉第定律法

线圈上任何位置通过线圈的磁通量为

其正负取决于表面的垂直线是否跟 B 同一方向，或相反方同。如果表面垂直线跟感应电流的 B 同一方向，式子为负。此时通量的时间导数（使用微分的链式法则或莱布尼茨定则的通用形式求出）为：

（其中 v = d x C /d t 为线圈于 x 方向的运动速率），所以

跟之前一样。

这两种方法一般来说都一样，但视乎例子而定，其中一种有时可能会比较实用。

例二：均匀磁场中的运动环路

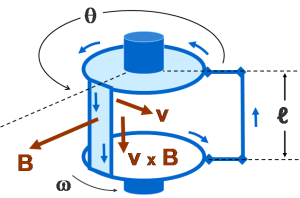
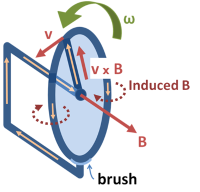
图四：矩形线圈以角速率ω转动，其所处的磁场 B 大小固定，并向外呈放射状指出。上下两块碟片的边沿会导电，而电流则由旁边的电刷收集。

图四为由上下两块带导电边沿的碟片所组成的转轴，上面的电线环路垂直地连接着两块碟片。整组装置在磁场中旋转，该磁场向外呈放射状指出，但其大小不随方向变化。一向外的回路从边沿上把电流收集起来。在收集回路的位置上，向外的磁场与回路位于同一个平面上，因此收电回路并不对电路的磁通量造成影响。电动势可直接求出，或使用上文的法拉第定律求出。

洛伦兹力法

这个案中，在移动环路中那两根垂直的电线里，洛伦兹力向下驱动着电流，因此电流从上碟片流向下碟片。在碟片的导电边沿内，洛伦兹力与边沿垂直，所以边沿上并没有电动势，环路中的水平部分也没有。电流通过外加的回路从下边沿传到上边沿，而该回路位于磁场的平面上。因此，回路中的洛伦兹力与回路平行，在这回路中并没有生成电动势。穿过电流通道，到达电流反方向流动的地方，功只在移动环路垂直电线中抵抗洛伦兹力，其中

因此电动势为

其中ℓ为环路中的垂直长度，与角转动率相关的速度可由 v = r ω求出，而 r = 碟片半径。注意，在 任何 跟环路转动并连接上下边沿的路径中，所作的功都 一样 。

法拉第定律法

一个直觉上很吸引但错误的通量定则使用法是，将通过电流的通量当成只是Φ B = Bw ℓ，其中 w 为移动环路的宽度。这数目与时间没有关系，所以这方法会不正确地预测出无生成电动势。这套论述的缺陷在于它并没有考虑到整个电路，而整个电路是闭合的环路。

使用通量定则时，我们必须顾及整个电路，其中包括通过上下碟片边沿的路径。我们可以选择一通过两道边沿及移动环路的任意闭合路径，而通量定则会找出该路径的电动势。任何有一部分连接移动环路的路径，都会表达到电路移动部分的相对运动。

作为一个路径例子，选择在上碟片按照转动方向，并下碟片按照转动反方向穿过电路（由图四的箭号表示）。在这情况下，对与回路成角θ的移动环路而言，圆柱体的一部分面积 A = r ℓθ为电路的一部分。这面积与磁场垂直，所以造成了这个大小的通量：

其中式子为 负 ，这是因为右手定则指出，电流环路所产生的磁场，与外加的磁场方向相反的缘故。由于这是通量中唯一一个跟随时间转变的部分，所以通量定则预测的电动势为

与使用洛伦兹力法的计算答案一致。

现在尝试不同的路径。跟随一条选择余分通过边沿的路径。那么耦合磁通量会随θ增加而 减少 ，但右手定则会指出把电流环路 加 到外加磁场上去，因此这条路径跟第一条路径的电动势相同。任何回路的组合都会对电动势产生相同的结果，因此跟随哪一条路径实际上并不重要。

直接从通量变量中求出

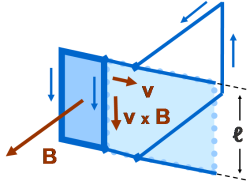
图五：图四的简化版本。环路在静止且均匀的磁场中，以速率 v 滑动。

以上使用闭合路径求电动势的方法，看起来是取决于路径几何的细节。相反地，使用洛伦兹力则没有这样的限制。所以有需要加深对通量定则的理解，有关路径等同及路径选取时的会漏掉的细节。

图五是图四的理想化版本，当中圆柱体被展开成了平面。同样的路径分析依然有效，但是还有一个可以简化的地方。电路中与时间无关的方面，并不能够影响通量随时间的变化率。例如，环路以均速滑动时，电流通过环路流动的细节，并不取决于时间。与其考虑求电动势时环路选取的细节，不如考虑环路移动时所扫过的 磁场面积 。这相当于找出电路通量的切断率。 这个说法提供了一个方法，可直接求出通量变化率，而不需要考虑电路上各种路径选取，随时间而变化的细节。跟使用洛伦兹力一样，很明显地，任何两条连接移动环路的路径，都会产生相同的通量变化率，不同之处只在于它们如何与环路相交。

图五中，单位时间内扫过的面积为 dA/dt = v ℓ，跟选取的环路细节无关，所以可经法拉第电磁感应定律求出电动势：

电路势的路径的不依赖性表明，如果滑动环路被实心导电板所取代，又或是更复杂的某种变形表面，分析都是一样的：找出电路移动部分扫过面积的通量。相近地，如果图四的移动环路被一360°的实心导电圆柱体所取代，扫过面积的计算就跟只有一个环路时是完全一样的。故此，对圆柱体及实心导电板的个案而言，法拉第定律所预测的电动势完全一样，更甚者，以有孔板为壁的圆柱体的个案也一样。但是注意，这个电动势所导致的流动电流是 不 一样的，因为电阻决定电流。

麦克斯韦-法拉第方程

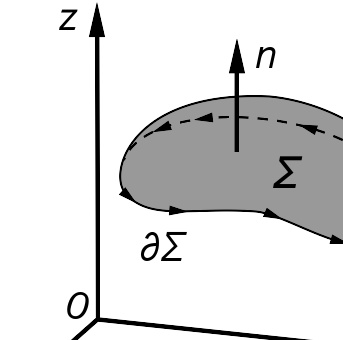
图六：开尔文-斯托克斯定理用图，其中曲面 Σ 的边界 ∂Σ ，其方向由向外的矢量 n 及右手定则规定。

变化中的磁场会生成电场；这个现象由麦克斯韦-法拉第方程描述：

其中：

这条方程是现代麦克斯韦方程组内的其中一条，很多时候被称为法拉第定律。然而，由于它只含有一个时间偏导数，它的应用只限于在随时间变化的磁场中静止电荷的情况。它并不能说明带电粒子在磁场中移动的电磁感应状况。

它可以用开尔文-斯托克斯定理写成积分形式：

其中把导数移至积分前这个动作，需要一与时无关的曲面 Σ （在这里被视为偏导数解释的一部分），见图六：

dℓ和d A 都具有正负模糊性；要得到正确的正负号，需要使用右手定则，解释详见开尔文-斯托克斯定理条目。对一平面Σ而言，曲线∂Σ的正路径元dℓ，其定义由右手定则所规定，就是当右手姆指跟表面Σ的垂直线 n 同一方向时，其他手指所指的那一个方向。

围绕着 ∂Σ 的积分叫曲线积分或路径积分。麦克斯韦-法拉第方程右边的曲面积分，是通过Σ的磁通量Φ B 的明确表达式。注意 E 的非零路径积分，跟电荷产生电场的表现不一样。由电荷生成的电场能以标量场的梯度表达，为泊松方程的解，并且路径积分为零。见梯度定理。

积分方程对通过空间的 任何 路径 ∂Σ 成立，也对任何以该路径为边界的的表面 Σ 成立。注意，但是已知在这方程里， ∂Σ 及 Σ 都 不 随时间而改变。这个积分形式不能用于 运动 电动势，因为 Σ 跟时间无关。注意这方程内并没有电动势 E {\displaystyle ^{\mathcal {E}}} ，所以确实不能够在不引入洛伦兹力的情况下计算出功。

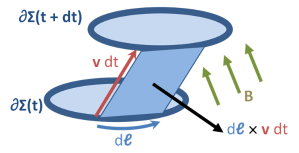
图七：由曲线 ∂Σ 的矢量元 d ℓ 在时间 dt 以速率 v 移动时扫过的面积。

使用完整的洛伦兹力计算电动势：

法拉第电磁感应定律的一个描述，比麦克斯韦-法拉第方程的积分形式更通用（见洛伦兹力），如下：

其中 ∂Σ ( t )为围着运动表面 Σ ( t )的闭合路径，而 v 为运动速率。见图二。注意上面用的是时间 常 导数，而不是时间 偏 导数，意指 Σ ( t )的时间差异必须被微分所包括。被积函数中，曲线 d ℓ 的元以速率 v 移动。

图七为磁力是如何促成电动势作出了诠释，而电动势就在上面方程的左边。曲线 ∂Σ 部分 d ℓ ，在时间 dt 以速率 v 移动时扫过的面积为（见矢量积的几何意义）：

所以在时间 dt 间通过 ∂Σ 为边的表面中这一部分的磁通量变量ΔΦ B 为：

如果我们把这些通过所有部分 d ℓ 的ΔΦ B 的作用加在一起，就可以得到法拉第定律对磁力的促成作用。也就是，这个项跟 运动 电动势有关系。

例三：移动观测者的视点

再次讨论图三的例子，但这次以移动观测者的参考系，带出电场与磁场间以及 运动 与 感应 电动势的密切关系。 假设一环路观测者与环路一起移动。观测者以洛伦兹力及法拉第电磁感应定律计算环路的电动势。由于这观测者与环路一起移动，观测者看不到环路的运动，以及零 v×B 。然而，由于磁场随 x 位置变化，所以观测者看到时间变强的磁场，也就是：

其中 k 为指向 z 方向的单位矢量。

洛伦兹力定律版本

麦克斯韦-法拉第方程指出移动观测者在 y 方向所见的电场 E y 可由下式表示（见旋度）：

下式使用了链式法则：

求解 E y ，准确到一个对环路积分没有作用的常数，得：

使用洛伦兹力定律，得一个电场分量，观测者于时间t得环路的电动势为：

这个结果跟静止观测者的个案一致，他看到的是中点 x C 移到 x C + vt 。然而，移动观测者的结果中，洛伦兹力看起来只有 电 分量，而静止观测者的则只有 磁 分量。

法拉第电磁感应定律

使用法拉第电磁感应定律，与 x C 一起移动的观测者看到磁通量的变化，但环路看起来并没有移动：环路的中心 x C 被固定了，这是因为观测者与环路一起移动着。通量则是：

其中右式为负，这是因为表面的垂直线与外加磁场各自指向相反的方向。现在从法拉第电磁感应定律得出的电动势是：

答案是一样的。时间导数走进了积分里面，这是因为积分的上下限并不取决于时间。又一次，链式定律被用于把时间导数转化成 x 导数。

静止观测者认为该电动势是 运动 电动势，而移动观测者则认为是 感应 电动势。

作为两种不同现象的法拉第定律

有些物理学家注意到法拉第定律是一条描述两种现象的方程：由磁力在移动中的电线中产生的 动生电动势 ，及由磁场转变而成的电力所产生的 感应电动势 。就像理查德·费曼指出的那样：

格里夫斯的书中也有类似陈述。

历史

法拉第定律最初是一条基于观察的实验定律。 后来被正式化，其偏导数的限制版本，跟其他的电磁学定律一块被列麦克斯韦方程组的现代亥维赛版本。

法拉第电磁感应定律是基于法拉第于1831年所作的实验。这个效应被约瑟·亨利于大约同时发现，但法拉第的发表时间较早。

见麦克斯韦讨论电动势的原著。

于1834年由波罗的海德国科学家海因里希·楞次发现的楞次定律，提供了感应电动势的方向，及生成感应电动势的电流方向。

应用

发电机

图八：法拉第碟片发电机。碟片以角速率ω旋转，在静磁场 B 中环行地扫过导电的半径。磁洛伦兹力 v×B ，沿着导电半径到导电边沿驱动着电流，并从那里经由下电刷及支撑碟片的轴完成电路。因此，电流由机械运动所产生。

由法拉第电磁感应定律因电路及磁场的相对运动所造成的电动势，是发电机背后的根本现象。当永久性磁铁相对于一导电体运动时（反之亦然），就会产生电动势。如果电线这时连着电负载的话，电流就会流动，并因此产生电能，把机械运动的能量转变成电能。例如，基于图四的 鼓轮发电机 。另一种实现这种构想的发电机就是法拉第碟片，简化版本见图八。注意使用图五的分析，或直接用洛伦兹力定律，都能得出使用实心导电碟片运作不变的这一结果。

在法拉第碟片这一例子中，碟片在与碟片垂直的均匀磁场中运动，导致一电流因洛伦兹力流到向外的轴臂里。明白机械运动是如何成为驱动电流的必需品，是很有趣的一件事。当生成的电流通过导电的边沿时，这电流会经由安培环路定理生成出一磁场（图八中标示为“Induced B”）。因此边沿成了抵抗转动的电磁铁（楞次定律一例）。在图的右边，经转动中轴臂返回的电流，通过右边沿到达底部的电刷。此一返回电流所感应的磁场会抵抗外加的磁场，它有 减少 通过电路那边通量的倾向，以此 增加 旋转带来的通量。因此在图的左边，经转动中轴臂返回的电流，通过左边沿到达底部的电刷。感应磁场会 增加 电路这边的通量， 减少 旋转带来的通量。所以，电路两边都生成出抵抗转动的电动势。尽管有反作用力，需要保持碟片转动的能量，正等于所产生的电能（加上由于摩擦、焦耳热及其他消耗所浪费的能量）。所有把机械能转化成电能的发电机都会有这种特性。

虽然法拉第定律经常描述发电机的运作原理，但是运作的机理可以随个案而变。当磁铁绕着静止的导电体旋转时，变化中的磁场生成电场，就像麦克斯韦-法拉第方程描述的那样，而电场就会通过电线推着电荷行进。这个案叫 感应电动势 。另一方面，当磁铁静止，而导电体运动时，运动中的电荷的受到一股磁力（像洛伦兹力定律所描述的那样），而这磁力会通过电线推着电荷行进。这个案叫 动生电动势 。（更多有关感应电动势、动生电动势、法拉第定律及洛伦兹力的细节，可见上例或格里夫斯一书。 ）

电动机

发电机可以“反过来”运作，成为电动机。例如，用法拉第碟片这例子，设一直流电流由电压驱动，通过导电轴臂。然后由洛伦兹力定律可知，行进中的电荷受到磁场 B 的力，而这股力会按佛来明左手定则订下的方向来转动碟片。在没有不可逆效应（如摩擦或焦耳热）的情况下，碟片的转动速率必需使得 dΦ B /dt 等于驱动电流的电压。

变压器

法拉第定律所预测的电动势，同时也是变压器的运作原理。当线圈中的电流转变时，转变中的电流生成一转变中的磁场。在磁场作用范围中的第二条电线，会感受到磁场的转变，于是自身的耦合磁通量也会转变（ d Φ B / dt ）。因此，第二个线圈内会有电动势，这电动势被称为 感应电动势 或 变压器电动势 。如果线圈的两端是连接着一个电负载的话，电流就会流动。

电磁流量计

法拉第定律可被用于量度导电液体或浆状物的流动。这样一个仪器被称为电磁流量计。在磁场B中因导电液以速率为v的速度移动，所生成的感应电压ε可由以下公式求出：

其中ℓ为电磁流量计中电极间的距离。

另见

法拉第吊诡

矢量分析

斯托克斯定理

串扰（由电感产生的电子干扰）

延伸阅读

有关 法拉第定律 一词各种用法的讨论：Tankersley and Mosca: Introducing Faraday"s law （英文）

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。