黑体辐射方程

黑体辐射本领

基尔霍夫(G. R. Kirchhoff)证明，对于任意一个物体，辐射本领 E ( ν ν --> , T ) {\displaystyle E(\nu ,T)} 与吸收率 A ( ν ν --> , T ) {\displaystyle A(\nu ,T)} 之比是一个与组成物体的物质无关的普适函数(以 f ( ν ν --> , T ) {\displaystyle f(\nu ,T)} 表示)

其中，辐射本领 E ( ν ν --> , T ) {\displaystyle E(\nu ,T)} 为单位时间内从辐射体表面的单位面积上发射出的辐射能量的频率分布，所以，在 Δ Δ --> t {\displaystyle \Delta t} 的时间，从 Δ Δ --> S {\displaystyle \Delta S} 面积上发射出频率在 ν ν --> − − --> − − --> ν ν --> + Δ Δ --> ν ν --> {\displaystyle \nu --\nu +\Delta \nu } 范围内的能量为 E ( ν ν --> , T ) Δ Δ --> t Δ Δ --> S Δ Δ --> ν ν --> {\displaystyle E(\nu ,T)\Delta t\Delta S\Delta \nu } 。因此 E ( ν ν --> , T ) {\displaystyle E(\nu ,T)} 的单位为 J / m 2 {\displaystyle J/m^{2}} ，可以证明，黑体辐射本领与辐射体的能量密度分布 u ( ν ν --> , T ) {\displaystyle u(\nu ,T)} 的关系为

u ( ν ν --> , T ) {\displaystyle u(\nu ,T)} 的单位为 J ⋅ ⋅ --> s / m 3 {\displaystyle J\cdot s/m^{3}} 吸收率 A ( ν ν --> , T ) {\displaystyle A(\nu ,T)} 则为照到物体上的辐射能量分布被吸收的份额，由于黑体的吸收率为1，所以它的辐射本领

这意味着黑体辐射本领等价于普适函数（与物质无关） 同时也可以以用 E ( λ λ --> , T ) {\displaystyle E(\lambda ,T)} 来表达辐射本领

E ( λ λ --> , T ) {\displaystyle E(\lambda ,T)} 的单位为 J / m 3 ⋅ ⋅ --> s {\displaystyle J/m^{3}\cdot s}

黑体辐射的普朗克公式

用于描述在任意温度 T {\displaystyle T\,} 下，从一个黑体中发射的电磁辐射的辐射率与电磁辐射的频率的关系公式。这里辐射率是频率 ν ν --> {\displaystyle \nu } 的函数：

各个物理量的意义

黑体辐射的维恩位移定律

维恩位移定律表述了不同温度的黑体波谱之间的联系。一旦某一个温度下的黑体波谱形状已知，则可通过维恩位移定律推导出同一黑体在其它温度下的波谱形状。

维恩位移定律计算出黑体辐射强度达到最大时的波长， λ λ --> m a x {\displaystyle \lambda _{\mathrm {max} }} ，这个物理量只和黑体的温度相关：

其中b为比例常数，称为维恩位移常数，数值等于2.897 7721(26) × 10 m K（2010年国际科技数据委员会（英语：CODATA）推荐值，括号中为68.27%置信度下的不确定尾数）。

注意到强度的峰值可以表达为单位波长强度或是单位频率强度，在维恩位移定律中使用的是单位波长强度的表达式，而在上面的普朗克黑体辐射定律中则使用的是单位频率强度。单位频率能量达到最大时的波长为

黑体辐射的斯特藩-玻尔兹曼定律

这条定理指出，一个黑体表面单位面积放出的能量正比于其绝对温度的4次方：

其中 j ⋆ ⋆ --> {\displaystyle j^{\star }} ：单位面积所放出的总能量，[J ]T {\displaystyle T}  :黑体的绝对温度，[K ]σ σ --> {\displaystyle \sig斯特藩-玻尔兹曼常数玻尔兹曼常数，

人体的辐射

黑体辐射同样适用于人体，因为人体的一部分能量以电磁波的形式散射出体表，其中大部分为红外线。

净放射功率是吸收功率和放出功率的差值：

代入黑体辐射的斯特藩-玻尔兹曼定律：

人体的表面积约为2平方米，皮肤和大多数衣物（非金属材质）中，远红外线热发射率基本相同。皮肤的温度大概为33°C，但在约为20°C的环境温度影响下，衣物会使体表温度降为大约28°C。因此，人体的净放射功率约为

人体一天所放出的总能量大约为9000千焦，或者为2000千卡。一个40岁的成年人的基础代谢率约为35千卡/（米·小时），即为1700千卡每天（以2平方米为基准）。实际上即便是静坐的成年人每日的平均代谢率也比基础代谢率高出约50%到70%。

热对流和体液蒸发也是人体散失能量的重要因素。因为努塞尔特数远远大于单一个体，所以热传导可以忽略。蒸发（汗液）这个要素只有在热辐射和热对流在某个恒温环境内不起主导因素时才给予考虑。自由热传导率尽管比辐射率小，但是也是可以进行比较的。因此，人体在静止凉爽的环境中散失的总热能的三分之二是由于热辐射导致的。由于使用了很多假设情况下的近似值，所以这个结果只能算是粗略的估计。人体周围的空气运动所引起的对流或是体液蒸发同样和热辐射一样是导致体能流失的重要因素。

如果在人体这个黑体上使用维恩位移定律，可以得到人体放出辐射的波长峰值为：

这个结果可以解释为什么人体热像仪的波长一般设为非常灵敏的7000到14000纳米。

行星和其卫星之间的热力学关系

黑体辐射定理的应用之一是用于概略的估计一个行星的温度。其表面可能由于温室效应而比估计温度高。

因素

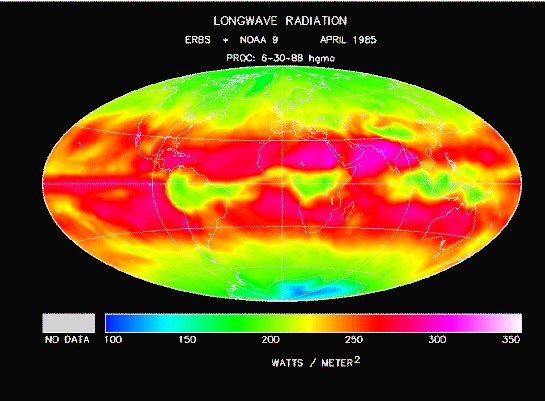
  地球（云层，大气和地面）的长波热辐射强度

行星的温度主要和以下几个因素相关：

外来的辐射（比如来自某个恒星）

本身放出的辐射（比如地球自身红外辐射）

反照率（行星反射的辐射）

温室效应（只针对有大气的行星）

行星自身产生的能量（由于放射性衰变，潮汐加热和克赫历程）

所有的辐射，无论是行星内部产生的，其他恒星还是其本身放出的，对行星的温度都有很重要的影响。以下的推导即着重讨论辐射。

推导

首先使用斯特藩-玻尔兹曼定律得到太阳放射出的总功率（能量/秒）：

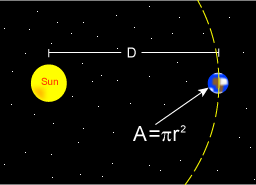
可以认为地球受到太阳照射的地区仅等于一个二维的圆形面积而非整个球面。

其中

太阳平均的向各个方向放出能量，因此，地球实际上只是接受到其中很小的一部分。这部分能量为（指接触到大气层外部）：

其中

由于本身的高温，太阳发出的射线大多数属于紫外线和可见光（UV-Vis）频率范围。在这个频率范围内，地球会反射一部分能量，其数量为 α α --> {\displaystyle \alpha } ，即地球对UV-Vis范围射线的反照率。反过来，即地球吸收了 1 − − --> α α --> {\displaystyle 1-\alpha } 的太阳光，并反射了剩下的。地球和其大气层所吸收的能量为：

虽然地球仅仅以一个面积为 π π --> R 2 {\displaystyle \pi R^{2}} 的圆形区域进行吸收，但是它同时以一个球体的形态向各个方向放出能量。假设地球是一个完全黑体，它将遵循斯特藩-玻尔兹定理：

其中 T E {\displaystyle T_{E}} 是地球的温度。由于地球的温度明显低于太阳，其放射的多为光系的红外线（IR）部分。在这个频率范围内，地球会放出黑体总放射波的一部分，大约为 ϵ ϵ --> ¯ ¯ --> {\displaystyle {\overline {\epsilon }}} ， ϵ ϵ --> ¯ ¯ --> {\displaystyle {\overline {\epsilon }}} 是红外线频率的平均放射率。因此地球和其大气层实际放出的能量为：

假设地球处于热平衡，则吸收的能量等于放射的能量：

代入所有关于太阳和地球能量的表达式（1-5）可以得到：

换句话说，考虑到所有的估计值，地球的温度与下列因素有关：太阳的表面温度，太阳的半径，日地间距，以及地球的反照率和红外发射率。

地球的温度

如果我们代入对太阳和地球的测量值：

并将平均放射率设为单位量，我们可以得到地球的”有效温度“为：

这个温度值是基于地球是一个完全黑体的假设，忽略温室效应并认为地球的反照率完全不变的基础上得到的。而实际上地球仅是非常接近一个完美黑体，所以我们必须将估计温度定为比有效温度高出好几度。如果我们想要估计地球在没有大气层的情况下的温度，我们可以使用月球的反照率和发射率进行计算。月球的反照率和发射率大约为0.1054和0.95， 因此，可以得到这种情况下的温度约为1.36 °C. 地球的平均反照率的估计值在0.3–0.4之间，由此我们可以得到不同的估计温度。进行计算时相较于太阳的温度，尺寸和日地距离，人们更加常用日照常量（总日照量密度）。比如使用0.4为反照率并使用日照量密度1400 W m，可以得到约为245K的地球温度。同理，如果使用0.3的反照率以及1372 W m的日照常量，地球温度为255 K。

运动黑体的多普勒效应

多普勒效应是著名的物理现象，人们用它来描述当一个光源对观察者作相对运动时，其光线频率的变化。若一单色光源的发射频率为f，则当它相对观察者做相对运动时，观察者看起来其频率为f"：

其中v是这个光源对观察者的相对速度，θ是速度向量和观察者及光源间连线的夹角，c为光速。上面的公式为总公式，还可以从其得到一些更简单的特殊例子，如光源直接向观察者移动（θ = π） 或是离开观察者（θ = 0），当然其移动速度远远小于c。

参阅

盒中气体

黑体

普朗克黑体辐射定律

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。