弱电相互作用-族谱新闻-族谱网

弱电相互作用

2020-10-16

出处：族谱网

作者：阿族小谱

浏览:914次

转发:0次

评论:0

数学表述图为已知基本粒子的弱同位旋T3及弱超荷YW的模式，图中标有电荷Q及弱混合角。中性的希格斯场（圆圈内）在打破电弱对称后，就能与其他粒子相互作用，从而产生质量。希格斯场的三个分量则成为具质量的W及Z玻色子的一部分。数学上统一电磁作用及弱作用是经由一个SU(2)×U(1)的规范群。当中对应的零质量规范玻色子分别是三个来自SU(2)弱同位旋的W玻色子(W+、W0和W−)以及一个来自U(1)弱超荷的B玻色子。在标准模型里W±和Z0玻色子和光子是经由SU(2)×U(1)Y的电弱对称性自发对称破缺成U(1)em所产生的，此一过程称作希格斯机制（见希格斯玻色子）。U(1)Y和U(1)em都属于U(1)群，但两者不同；U(1)em的生成元是电荷Q=Y/2+I3，而其中Y是U(1)Y（叫弱超荷）的生成元，I3（弱同位旋的一个分量）则是SU(2)的其中一个生成元。自发对称破缺使W0和B玻色子组合成两种不...

数学表述

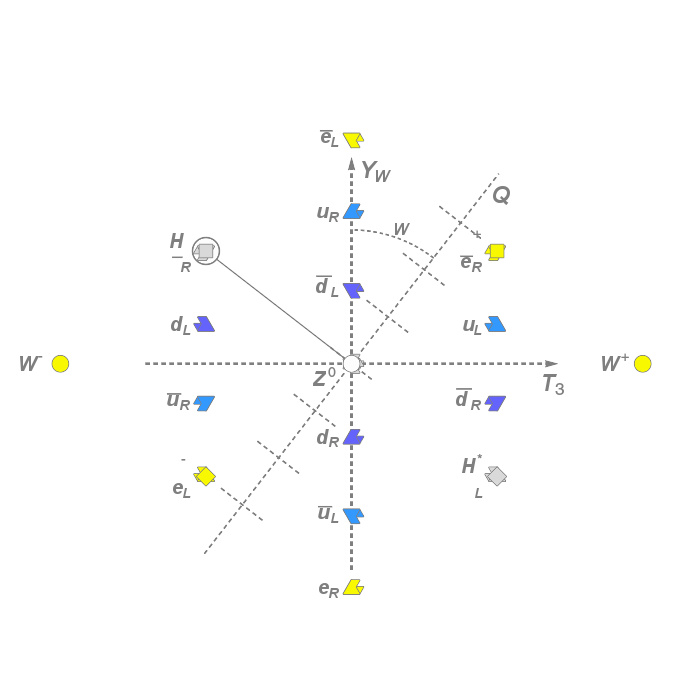
图为已知基本粒子的弱同位旋T 3 及弱超荷Y W 的模式，图中标有电荷Q及弱混合角。中性的希格斯场（圆圈内）在打破电弱对称后，就能与其他粒子相互作用，从而产生质量。希格斯场的三个分量则成为具质量的W及Z玻色子的一部分。

数学上统一电磁作用及弱作用是经由一个SU(2)×U(1)的规范群。当中对应的零质量规范玻色子分别是三个来自 SU(2)弱同位旋的W玻色子( W + 、 W 0 和 W − )以及一个来自U(1)弱超荷的B 玻色子。

在标准模型里W ± 和 Z 0 玻色子和光子是经由SU(2)×U(1) Y 的电弱对称性自发对称破缺成U(1) em 所产生的，此一过程称作希格斯机制（见希格斯玻色子）。U(1) Y 和U(1) em 都属于U(1)群，但两者不同；U(1) em 的生成元是电荷Q=Y/2+I 3 ，而其中Y是U(1) Y （叫弱超荷）的生成元，I 3 （弱同位旋的一个分量）则是SU(2)的其中一个生成元。

自发对称破缺使 W 0 和B 玻色子组合成两种不同的玻色子： Z 0 玻色子和光子(γ)。如下：

其中θ W 为弱混合角。对称破缺使得代表粒子的轴在( W 0 , B )平面上旋转，其旋转角为θ W （见右图）。对称破缺同时使得 Z 0 和 W ± 的质量变得不一样（它们的质量分别以M Z 和M W 表示）：

电磁作用与弱力在对称破缺后变得不同，是因为希格斯玻色子的Y及I 3 ，可以组成一个答案为零的线性组合：U(1) em 的定义生成元（电荷）正是这个组合，所以电磁作用不与希格斯场作用，亦因此保留对称性（光子零质量）。

拉格朗日量

自发对称破缺之前

弱电相互作用的拉格朗日量在自发对称破缺之前分成四个部分：

L g {\displaystyle {\mathcal {L}}_{g}} 项描述三种W粒子及一种B粒子的相互作用：

其中 W a μ μ --> ν ν --> {\displaystyle W^{a\mu \nu }} ( a = 1 , 2 , 3 {\displaystyle a=1,2,3} )及 B μ μ --> ν ν --> {\displaystyle B^{\mu \nu }} 分强度弱同位旋及弱超荷的场强度张量。

L f {\displaystyle {\mathcal {L}}_{f}} 为标准模型费米子的动能项。规范玻色子与费米子间的相互作用是由共变导数所描述的。

其中下标 i {\displaystyle i} 代表费米子代，根据爱因斯坦求和约定，各项中重复的下标会把三代的结果都加起来，而 Q {\displaystyle Q} 、 u {\displaystyle u} 和 d {\displaystyle d} 分别代表夸克的左手性双重态、右手性上单重态和右手性下单重态， L {\displaystyle L} 和 e {\displaystyle e} 则代表轻子的左手性双重态和右手性电子单重态。注意右手性中微子是不参与弱相互作用的，因此轻子比夸克少一个项。

L h {\displaystyle {\mathcal {L}}_{h}} 描述希格斯场F：

L y {\displaystyle {\mathcal {L}}_{y}} 负责提供汤川相互作用，它会把希格斯场所产生的真空期望值变成质量，

自发对称破缺之后

在希格斯玻色子获得真空期望值后，拉格朗日量

动能项 L K {\displaystyle {\mathcal {L}}_{K}} 含有拉格朗日量中所有的二次项，当中包括动力项（偏微分）和质量项（明显地没有出现于对称破缺之前的拉格朗日量之中）。

其中总和把理论中费米子（夸克和轻子）的各代都加起来，而场 A μ μ --> ν ν --> {\displaystyle A_{\mu \nu }^{}} 、 Z μ μ --> ν ν --> {\displaystyle Z_{\mu \nu }^{}} 、 W μ μ --> ν ν --> − − --> {\displaystyle W_{\mu \nu }^{-}} 及 W μ μ --> ν ν --> + ≡ ≡ --> ( W μ μ --> ν ν --> − − --> ) † † --> {\displaystyle W_{\mu \nu }^{+}\equiv (W_{\mu \nu }^{-})^{\dagger }} 的形式如下：

拉格朗日量中的中性流分量 L N {\displaystyle {\mathcal {L}}_{N}} 与载荷流分量 L C {\displaystyle {\mathcal {L}}_{C}} ，就是费米子与规范玻色子间的相互作用。

其中电磁流 J μ μ --> e m {\displaystyle J_{\mu }^{em}} 及中性弱流 J μ μ --> 3 {\displaystyle J_{\mu }^{3}} 分别为

及

q f {\displaystyle q_{f}^{}} 和 I f 3 {\displaystyle I_{f}^{3}} 分别是费米子的电荷和弱同位旋。

拉格朗日量的载荷流部分如下：

L H {\displaystyle {\mathcal {L}}_{H}} 代表希格斯场的三点及四点自身相互作用。

L H V {\displaystyle {\mathcal {L}}_{HV}} 代表规范矢量玻色子的希格斯相互作用。

L W W V {\displaystyle {\mathcal {L}}_{WWV}} 代表规范场的三点自身相互作用。

L W W V V {\displaystyle {\mathcal {L}}_{WWVV}} 代表规范场的四点自身相互作用。

而 L Y {\displaystyle {\mathcal {L}}_{Y}} 则代表费米子与希格斯场间的汤川相互作用。

注意各个弱耦合里 1 − − --> γ γ --> 5 2 {\displaystyle {\frac {1-\gamma ^{5}}{2}}} 这个因子：这些因子会把旋量场的左手性分量投映出来。因此（对称性破缺后的）电弱理论一般由被称为手征理论。