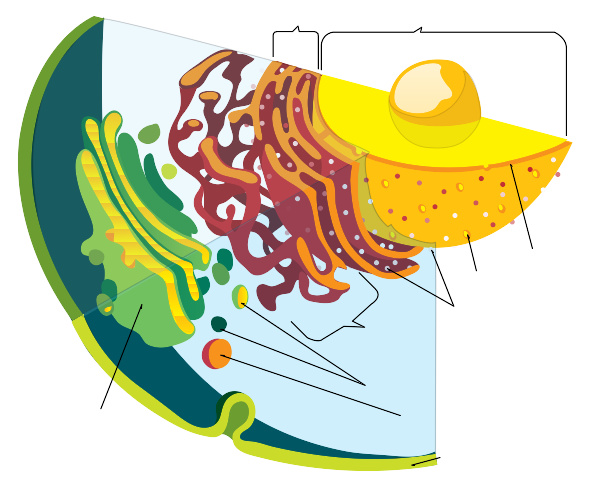
真核生物的分类传统分类在古时候，人们就已认识到动物和植物应分为两类。在林奈建立分类阶元时，虽然存在一定疑惑但还是把真菌划为两界说中的植物界。而后来的学者把真菌独立成一界，即把真核生物分为三界：植物界、动物界、真菌界。显微镜发明后，所发现的许多原生生物根据是自养还是异养，划分为原生植物与原生动物，分别归入植物界与动物界。而海克尔增加了原生生物界，即把真核生物分为四界。在20世纪80年代之前，单细胞的原生生物的分类还处于很混乱的阶段，直到DNA测序技术的成熟使系统发生学出现，改变了这一状况，也使人们开始重新谱写真核生物的分类。2005年国际原生生物学家协会分类根据系统发生学的研究，根据进化分支上的同源性，2005年的国际原生生物学家协会（英语：InternationalSocietyofProtistologists）提出了一种在当时被普遍接受的真核生物分类方法，分作六类（supergroup...

参考文献参见RNA

共同特征代谢和遗传是最大两点，但在复杂生命中需要更多属性来定义，只是这些属性并非普遍存在，详见下。例如病毒就是相当特殊的生命表现形式。生物的共有属性主要有四个，一般我们会包含：新陈代谢（化学物质的生成与分解）生长发育（收集、储存资源）繁殖（遗传物质的传递，但很多生物的个体无法进行繁殖——尽管它们所属的物种可以繁殖）适应（外部物理环境变化不至于影响体内的化学变化）较不明显的有其他三个应激性（但有些生物无法直接对刺激产生反应，如植物没有神经）运动（许多生物无法独立移动）组织性（生物间如雌雄的互动、护幼、共生、社会组织等等）化学生物体是复杂的化学系统，其作用在维持生物体的生存及发展，以及繁衍后代。生物化学主要研究生物体内的化学现象。整个生物体的现象可以决定生物是否可以适合其环境，也决定了其中DNA内的基因是否可以继续存续。生物体的代谢及其他许多内部机能都和化学反应有关，特别那些有关大型有机分子的...

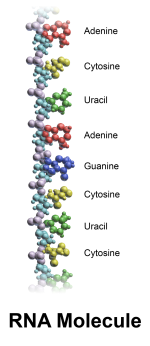
与DNA的比较RNA分子中的含氮碱基50S核糖体亚单位的3D结构示意图。rRNA以土黄色表示，蛋白质以蓝色表示。活性位点为rRNA的一个小片段，以红色标出RNA的分子结构与DNA非常相似，但是，两者有以下三个主要不同点：与DNA相似，大部分有生物活性的RNA，包括mRNA、tRNA、rRNA、snRNA，以及其他一些非编码RNA，虽然是单链，但含有自我互补的序列，能使得它们能进行折叠，形成互补双链接构（茎）。对RNA的分析表明，它们有着相对更复杂的结构。和DNA不同，RNA的二级结构并不是单纯的双螺旋，而由一系列短的二级结构构成。通过这些短的二级结构的组合，RNA甚至可以拥有与蛋白质相似的结构，并像酶那样催化化学反应（这样的RNA被称为核酶）。比如，对核糖体进行分析表明，其催化成肽反应的活性位点完全由RNA构成。结构siRNA（小干扰RNA）中的碱基互补配对（图中省略了氢原子）RNA的单体...

例子纵览线性算子设V和W是向量空间并设T是从V到W的线性变换。如果0W是W的零向量，则T的核是单元素集合{0W}的前像；就是说V的由被T映射到元素0W的那些V的元素构成的子集。核通常指示为“kerT”，或者：因为线性变换保持零向量，V的零向量0V必须属于核。变换T是单射的，当且仅当它的核只是单元素集合{0V}。kerT显然总是V的子空间。因此，它使谈论商空间V/(kerT)有意义。对向量空间的第一同构定理声称这个商空间自然同构于T的像（它是W的子空间）。作为结论，V的维度等于核的维度加上像的维度。如果V和W是有限维的向量空间，并且基已经选择好了，则T可以用矩阵M描述，而这个核可以通过解齐次线性方程组Mv=0来计算。在这种表示中，核对应于M的零空间。零空间的维度叫做M的零化度（nullity）由M的纵列数减去M的秩得到，这是秩-零化度定理的结论。解齐次微分方程经常涉及计算特定微分算子的核。例...