定律的引出和表述

瓦尔特·能斯特

定律的数学表述

观察一个内部热力学平衡的封闭系统。由于系统处于平衡，其内部不会进行不可逆过程，因而全系统的熵的增加为零。

绝对零度是不可达到的

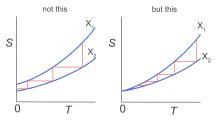
当温度趋近绝对零度时，只有熵不是常值时，才能通过有限的过程达到，否则是不可能的

由热力学第三定律我们可以知道，无论通过多么理想化的过程，都不可能通过有限次数的操作将任意一个热力学系统的温度降到绝对零度。

热容量

蒸汽压

潜热

³He和⁴He的熔化曲线在有限压强下都会延伸趋近绝对零度。在熔化曲线上各点表述的条件下，系统会处于固液相平衡。而热力学第三定律要求在温度为绝对零度时（如果能达到），系统的熵（无论物质处于何种物态）为定值。由此，可以推出在绝对零度时（如果能达到），系统熔化的潜热是零。另外，在这一结论基础上，通过克劳修斯－克拉佩龙方程可以得到，熔化曲线在绝对零度点的切线斜率为零。

热膨胀系数

热膨胀系数定义为α α -->V=1Vm(∂ ∂ -->Vm∂ ∂ -->T)p.{\displaystyle \alpha _{V}={\frac {1}{V_{m}}}\left({\frac {\partial V_{m}}{\partial T}}\right)_{p}.}。

考虑麦克斯韦关系，(∂ ∂ -->Vm∂ ∂ -->T)p=− − -->(∂ ∂ -->Sm∂ ∂ -->p)T{\displaystyle \left({\frac {\partial V_{m}}{\partial T}}\right)_{p}=-\left({\frac {\partial S_{m}}{\partial p}}\right)_{T}}

和式(8)取 X为p时的情况，

可以看出limT→ → -->0α α -->V=0.{\displaystyle \lim _{T\rightarrow 0}\alpha _{V}=0.}，即对于任何材料，当温度趋于绝对零度时，其热膨胀系数也会趋于零。

历史

2017年3月14日，伦敦大学学院物理学者强纳森·欧本海姆（Jonathan Oppenheim）与路易斯·马撒纳斯（Lluis Masanes）发表论文首次数学证实绝对零度不能达到原理，并且设定了冷却热力系统的速度的限制。

参考文献

^范康年, 《物理化学》第二版, 高等教育出版社, 2005, ISBN 7-04-016767-0.  

^Masanes, LLuis; Oppenheim, Jonathan.A general derivation and quantification of the third law of thermodynamics. Nature Communications. 2017-03-14. 

参阅

热力学

热力学第零定律

热力学第一定律

热力学第二定律

熵

余熵

基态

绝热过程

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。