



卡诺定理
证明
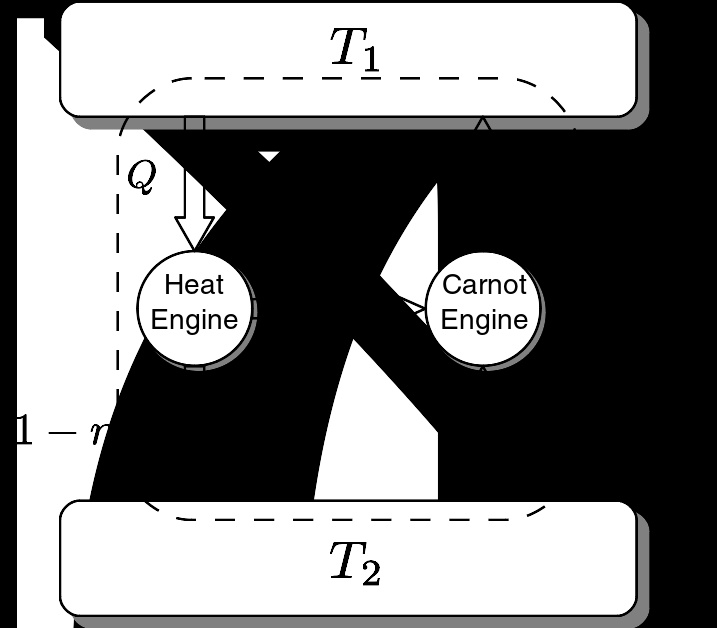
证明卡诺定理
此定理可用以下的方式,针对不可逆热机及可逆热机的情形进行证明
不可逆热机
假设一不可逆热机,其热源为T1{\displaystyle T_{1}}及T2{\displaystyle T_{2}},其热效率为η η -->{\displaystyle \eta },此热机和一个效率为η η -->′ ′ -->{\displaystyle \eta \prime }的逆卡诺热机,依右图的方式组合成一个热力学循环,不可逆热机产生的功为逆卡诺热机的工作来源。
若η η -->=η η -->′ ′ -->{\displaystyle \eta =\eta \prime },则此热力学循环对系不可逆性何影响,与不可逆性矛盾,因此不成立。
若η η -->>η η -->′ ′ -->{\displaystyle \eta >\eta \prime },则此热力学循环可由低温热源T2{\displaystyle T_{2}}取出
的能量,将此能量释放到高温热源T1{\displaystyle T_{1}},且不引起其他变化,违反热力学第二定律,也无法成立。
因此结论为η η -->′ ′ -->{\displaystyle \eta ,不可逆热机的效率η η -->{\displaystyle \eta }较卡诺热机的效率η η -->′ ′ -->{\displaystyle \eta \prime }低。
可逆热机
对于可逆热机的例子,可依类似的方式得到η η -->⩽ ⩽ -->η η -->′ ′ -->{\displaystyle \eta \leqslant \eta \prime }的结果。
若用待测的可逆热机当成逆热机,和一般的卡诺热机形成一个热力学循环,也可得到η η -->′ ′ -->⩽ ⩽ -->η η -->{\displaystyle \eta \prime \leqslant \eta }的结果。
由于上述二式需同时成立,可得以下的式子
应用在燃料电池上
有关卡诺定理是否能应用在燃料电池,至今科学家还没有达成共识。凯斯西储大学的教授认为“由于燃料电池中的电化学反应不涉及将热能转换为机械能,因此不受卡诺定理的限制”。不过K. T. Jacob及Saurabh Jain则认为“传统的观点认为燃料电池不受卡诺定理的限制,不过最近几篇论文都认为热力学第二定律不但限制热机的效率,也以同样方式限制燃料电池的效率”
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。

- 有价值
- 一般般
- 没价值








推荐阅读
关于我们

APP下载


















