历史

阿尔法粒子散射的实验完成于1909年。在那时代，原子被认为类比于梅子布丁（物理学家约瑟夫·汤姆孙提出的），负电荷（梅子）分散于正电荷的圆球（布丁）。假若这梅子布丁模型是正确的，由于正电荷完全散开，而不是集中于一个原子核，库仑位势的变化不会很大，通过这位势的阿尔法粒子，其移动方向应该只会有小角度偏差。

在卢瑟福的指导下，盖革和马士登发射阿尔法粒子射束来轰击非常薄、只有几个原子厚度的金箔纸。然而，他们得到的实验结果非常诡异，大约每8000个阿尔法粒子，就有一个粒子的移动方向会有很大角度的偏差（甚至超过 90°）；而其它粒子都直直地通过金箔纸，偏差几乎在2°到3°以内，甚至几乎没有偏差。从这结果，卢瑟福断定，大多数的质量和正电荷，都集中于一个很小的区域（这个区域后来被称作“原子核”）；电子则包围在区域的外面。当一个（正价）阿尔法粒子移动到非常接近原子核，它会被很强烈的排斥，以大角度反弹。原子核的小尺寸解释了为什么只有极少数的阿尔法粒子被这样排斥。

卢瑟福对这奇异的结果感到非常惊异。正如同他后来常说的：“这就好像一张卫生纸射出一枚15吋的炮弹，炮弹却弹回来打中你一样。”

卢瑟福计算出原子核的尺寸应该小于 10− − -->14m{\displaystyle 10^{-14}m\,\!} 。至于其具体的数值，卢瑟福无法从这实验决定出来。关于这一部分，请参阅后面的“原子核最大尺寸”一节。

微分截面

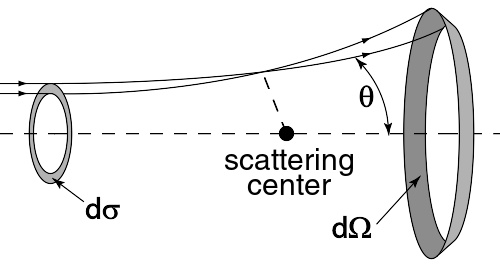
一个粒子的排斥散射。所有通过左边圆环 dσ σ -->{\displaystyle d\sigma \,\!} 的粒子，感受到位势的作用，必定会通过右边圆环 dΩ Ω -->{\displaystyle d\Omega \,\!} 。

卢瑟福计算出来的微分截面是

其中，σ σ -->{\displaystyle \sigma \,\!截面是截面，Ω Ω -->{\displaystyle \Omega \立体角} 是立体角，q{\displaystyle q\,\!} 是阿尔法粒子的电荷量，Q{\displaystyle Q\,\!} 是散射体的电荷量，ϵ ϵ -->0{\displaystyle \epsilon _{0}\,\!} 是真空电容率，E{\displaystyle E\,\!} 是能量，θ θ -->{\displaystyle \theta \,\!} 是散射角度。

原子核最大尺寸

假设阿尔法粒子正面碰撞于原子核。阿尔法粒子所有的动能（mv02/2{\displaystyle mv_{0}^{2}/2\,\!}），在碰撞点，都被转换为势能。在那一刹那，阿尔法粒子暂时是停止的。从阿尔法粒子到原子核中心的距离 b{\displaystyle b\,\!} 是原子核最大尺寸。应用库仑定律，

其中，m{\displaystyle m\,\!} 是质量，v0{\displaystyle v_{0}\,\!} 是初始速度。

重新编排，

阿尔法粒子的质量是 m=6.7× × -->10− − -->27 kg{\displaystyle m=6.7\times 10^{-27}\ kg\,\!} ，电荷量是 q=2× × -->(1.6× × -->10− − -->19) C{\displaystyle q=2\times (1.6\times 10^{-19})\ C\,\!} ，初始速度是 v0=2× × -->107 m/s{\displaystyle v_{0}=2\times 10^{7}\ m/s\,\!} ，金的电荷量是 Q=79× × -->(1.6× × -->10− − -->19) C{\displaystyle Q=79\times (1.6\times 10^{-19})\ C\,\!} 。将这些数值代入方程，可以得到撞击参数b=2.7× × -->10− − -->14 m{\displaystyle b=2.7\times 10^{-14}\ m\,\!} （真实半径是 7.3× × -->10− − -->15 m{\displaystyle 7.3\times 10^{-15}\ m\,\!} ）。这些实验无法得到真实半径，因为阿尔法粒子没有足够的能量撞入 27 fm{\displaystyle 27\ fm\,\!} 半径内。卢瑟福知道这问题。他也知道，假若阿尔法粒子真能撞至 7.3 fm{\displaystyle 7.3\ fm\,\!} 半径，直接地击中金原子核，那么，在高撞击角度（最小撞击参数 b{\displayst双曲线 b\,\!} ），由于位势不再是库仑位势，实验得到的散射曲线的样子会从双曲线改变为别种曲线。卢瑟福没有观察到别种曲线，显示出金原子核并没有被击中。所以，卢瑟福只能确定金原子核的半径小于 27 fm{\displaystyle 27\ fm\,\!} 。

1919 年，在卢瑟福实验室进行的另一个非常类似的实验，物理学家发射阿尔法粒子于氢原子核，观察到散射曲线显著地偏离双曲线，意示位势不再是库仑位势。从实验数据，物理学家得到撞击参数或最近离距（closest approach）大约为 3.5 fm{\displaystyle 3.5\ fm\,\!} 。更进一步的研究，在卢瑟福实验室，发射阿尔法粒子于氮原子核和氧原子核，得到的结果，使得詹姆斯·查德威克和工作同仁确信，原子核内的作用力不同于库仑斥力。

应用

现今，应用这些年累积的散射原理与技术，卢瑟福背散射谱学能够侦侧半导体内的重金属杂质。实际上，这技术也是第一个在月球使用的实地分析技术。在勘察者任务（surveyor mission）降落于月球表面后，卢瑟福背散射谱学实验被用来收集地质资料。

参阅

汤姆孙散射

散射理论

参考文献

Rutherford E.The Scattering of α and β Particles by Matter and the Structure of the Atom. Philosophical Magazine, Series 6. 1911, 21: 669–688. 

参阅

卢瑟福散射

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。