发展历史

弦理论的雏形是在1968年由 维内奇诺 （ 英语 ： Gabriele Veneziano ） （Gabriele Veneziano）发明。有说法称，他原本是要找能描述原子核内的强作用力的数学函数，然后在一本老旧的数学书里找到了有200年历史的欧拉贝塔函数，这函数能够描述他所要求解的强作用力。但根据维内奇诺本人的说法，这个函数是他多年努力的结果，而那些“偶然发现”以及“从数学书中发现”的传言令他本人很不高兴。 不久后李奥纳特·萨斯坎德发现，这函数可理解为一小段类似橡皮筋那样可扭曲抖动的有弹性的“线段”，这在日后则发展成“弦理论”。目前弦论学家普遍认为强子散射振幅公式是弦论的开端，此一公式即来自于Γ函数与B函数，描述两个强子一开始是两条弦，然后融合成一条，再分裂出两条。在这些弦扫过的区域称为世界面，可以用量子力学算这整个过程的概率振幅。

另外，同在CERN工作的铃木真彦（Mahiko Suzuki）几乎同时而又独立地查阅相关资料，并且也发现了贝塔函数，当他将该消息告诉CERN的一位资深物理学家后，得到的回应却是：“另一个年轻物理学家（即维内奇诺）已经在几个星期前发现了相同的函数。”并劝铃木不要发表他的结果。

弦论除了可以解释强作用力，也能消除点粒子的无穷大问题。由于粒子的相互作用可以用费曼图描述，然而粒子的相互作用点却等同于奇点，换句话说，它会引起无穷大的问题。虽然量子场论中的重整化理论可以解决无穷大，然而在量子的微观尺度，却是充满随机的量子涨落，结构层次的改变将使得重整化无法适用。这是因为广义相对论中传递引力的介质可以视为整体时空，当时空背景为量子尺度时，结构将会不稳定，且若将量子力学的计算方式强行套用在广义相对论则会产生限制。因此，若用弦来描述粒子相互作用的费曼图，基本上不会产生奇点，这是由于弦的运动轨迹是世界面。故弦论为量子引力的候选者，有望完成物理界所追求的万有理论。

虽然弦理论最开始是要解出强作用力的作用模式，但是后来的研究则发现了所有的粒子（含反粒子），如正反夸克，正反电子（电子、正电子），正反中微子等等，以及四种基本作用力粒子（胶子、中间玻色子、光子、引力子），都能用类似方法表示成一小段的不停振动的能量弦线，而各种粒子彼此之间的差异只是这弦线的长度、振动参数和形状的不同而已。

发展

玻色弦理论

最早期的弦论叫做玻色弦理论，南部阳一郎给予最早的作用量 ，但是该作用量在场论的框架内难以量子化。此后亚历山大·泊里雅科夫给予一个等效的作用量，其几何含义是把时空坐标视为一个世界面的标量场，并且在世界面上满足广义相对论的一般坐标变换规则。除此之外，如果要求这个作用量同时满足在外尔变化下不变，那么自然的会要求这个世界面是一个二维的曲面。

玻色弦理论是最简单的一个弦论的模型，它最重要的物理图像是认为物理粒子不是单纯的点粒子，而是由于弦的振动产生的激发态。显然它有很大的缺点，其一是它只简单描述标量玻色子，没有将费米子引入框架内；其二没有包含一般量子场论中的规范对称性；其三是当研究它的质量谱时候发现，它的真空态是一组质量平方小于零的不稳定快子。所有这些问题在推广到超弦理论后得到很好的解释。

开弦

1995年，加利福尼亚大学圣塔芭芭拉分校的约瑟夫·波尔钦斯基弦理论一个相当晦涩的特点。他发现开放的弦的端点（开弦）在陷在某些特别的时空区域时无法完全自由地移动。波尔钦斯基随后猜测这些特殊的空间正式被P膜所占据。这些“黏性”的膜就叫做狄利克雷-P-膜，或者D-P-膜。他的计算表明D-P-膜正是对弦端点施加的力的来源，目的是将其限制于其所存在的P维空间内。

闭弦

但不是所有的弦都属于P-膜。闭弦类似于引力子，可以随意在膜间移动。在四种力（强相互作用，弱相互作用，电磁相互作用和引力相互作用）的粒子中，引力子因此很特别。研究人员推测这或许就是为什么对其他三种力的研究都没有办法找到高维空间的存在。这三种力的媒介粒子就是将它们自己限制在P膜里的开弦。现阶段所需要做的就是对引力子进行更详实的研究来证明其他维度的空间的存在。

超弦理论

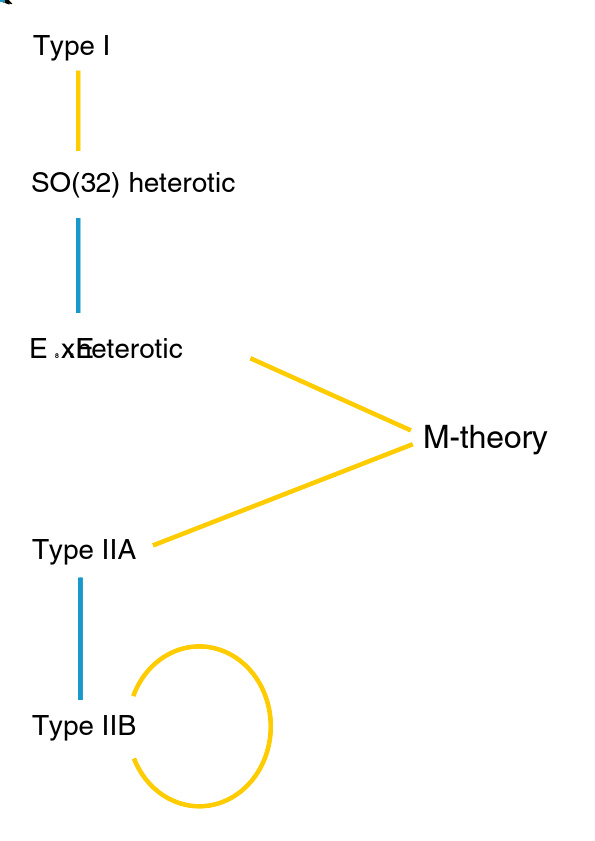
另外，“弦理论”这一用词所指的原本包含26维的玻色弦理论，和加入超对称性的超弦理论。在近日的物理界，“弦理论” 一般是专指“超弦理论”，为了方便区分，较早的“玻色弦理论”则以全名称呼。1990年代，受对偶性 (弦论)的启发，爱德华·维顿猜想存在一11维的M理论，他和其他学者找到强力的证据，显示五种不同版本的十维超弦理论与十一维超引力论其实应该是M理论的六个不同极限。这些发现带动了第二次超弦革命。

弦理论与大统一理论

弦理论会吸引这么多注意，大部分的原因是因为它很有可能会成为大统一理论。弦理论也可能是量子引力的解决方案之一，含有量很大。除了引力之外，它很自然的成功描述各式作用力，包含电磁力和自然界存在的其他各种作用力。超弦理论还包含组成物质的基本粒子之一的费米子。至于弦理论能不能成功的解释基于目前物理界已知的所有作用力和物质所组成的宇宙，这还是未知数。至今研究员仍未能找到一个弦论模型，其低能极限为标准模型。

额外维

额外维是相对于“四维时空”而提出的一个概念，一般泛指的是理论在四维时空基础上扩展出来的其它维度。

爱因斯坦提出宇宙是空间加时间组成的“四维时空”。1926年，德国数学物理学家西奥多·卡鲁扎在四维时空上再添加一个空间维，也就是添加一个第五维，把爱因斯坦的相对论方程加以改写，改写后的方程可以把当时已知的两种基本力即“电磁力”和“引力”很自然地统一在同一个方程中。至此，理论中存在额外添加的维度统称为“额外维”。超弦理论中是一维时间十维空间或九维空间。

D-膜

由于超弦理论的时空维数为10维，所以很自然的可以认为有6个额外的维度需要被紧化。当对闭弦紧化时，可以发现所谓的T对偶；而对开弦紧化则可以发现开弦的端点是停留在这些超曲面上的，并且满足狄利克雷边界条件。所以这些超曲面一般被称为“D膜”。 研究员称D膜的动力学为“矩阵理论”（M理论），是为“M”字来源之一。

物理或是哲学

在未获实验证实之前，弦理论是属于哲学的范畴，不能完全算是物理学。无法获得实验证明的原因之一是目前尚没有人对弦理论有足够的了解而做出正确的预测，另一个则是目前的高速粒子加速器还不够强大。

科学家们使用目前的和正在筹备中的新一代的高速粒子加速器试图寻找超弦理论里主要的超对称性学说所预测的超粒子。但是就算是超粒子真的找到了，这仍不能算是可以证实弦理论的强力证据，因为那也只是找到一个本来就存在于这个宇宙的粒子而已，不过这至少表示研究方向还不是错误的。

问题与争论

虽然历史上，弦理论是物理学的分支之一，但仍有一些人主张，弦理论目前不可实验的情况，意味着它应该（严格地说）被更多地归为一个数学框架而非科学。一个有效的理论，必须通过实验与观察，并被经验地证明。不少物理学家们主张要通过一些实验途径去证实弦理论。 一些科学家希望借助欧洲核子研究组织（CERN，Conseil European Pour Recherches Nucleaires）的大型强子对撞机，以获得相应的实验数据——尽管许多人相信，任何关于量子引力的理论都需要更高数量级的能量来直接探查。 此外，弦理论虽然被部分物理学家认同，但它拥有非常多的等可能性的解决方案。 因此，一些科学家主张弦理论或许不是可证伪的，并且没有预言的力量。

由于任何弦理论所作出的那些与其他理论都不同的预测都未经实验证实的，该理论的正确与否尚待验证。为了看清微粒中弦的本性所需要的能量级，要比目前实验可达到的高出许多。弦理论具有很多在数学上很有意思的特征（features of mathematical interest）并自然地包含了标准模型的大多数特性，比如非阿贝尔群与手征性费米子（chiral fermions）。因为弦理论在可预知的未来可能难以被实验证明，一些科学家 问，弦理论甚至是否应该被叫做一个科学理论。它现在还不能在波普尔的哲学含义中被证伪。但这也暗示了弦理论更多地被看做建设模型的框架。在同样的形式中，量子场论是一个框架。

弦理论的思想为物理学带来了一个建议上超越标准模型的巨大影响。例如，虽然超对称性是组成弦理论的重要一部分，但是那些与弦理论没有明显联系的超对称模型，科学家们也有研究。因此，如果超对称性在大型强子对撞机中被侦测到，它不会被看做弦理论的一个直接证明。然而，如果超对称性未被侦测出，由于弦理论中存在只有以更加更加高的能量才能看出超对称性的真空，所以它的缺乏不会证明弦理论是错误的。相反，如果日食期间观测到太阳的引力未使光按预测的角度偏转，那么爱因斯坦的广义相对论将被证明是错误的。实验证明了广义相对论的正确性。

在更数学的层次上，另一个问题是，如同很多量子场论，弦理论的很大一部分仍然是微扰地（perturbatively）用公式表达的（即为对连续的逼近，而非一个精确的解）。虽然非微扰技术有相当大的进步——包括猜测时空中满足某些渐进性的完整定义——一个非微扰的、充分的理论定义仍然是缺乏的。

物理学中，弦理论有关应用的一个中心问题是，弦理论最好的理解背景保存着大部分从“时不变的时空”得出的的超对称性潜在理论：目前，弦理论无法处理好时间依赖与宇宙论背景的问题。

前面提到的两点涉及一个更深奥的问题：在弦理论目前的构想中，由于弦理论对背景的依赖——它描述的是关于固定时空背景的微扰膨胀，它可能不是真正基础的。一些人把背景独立（background independence）看做对于一个量子引力理论的基础要求；自从广义相对论已经是背景独立的以来，尤其如此。

参见

超弦理论

对偶性 (弦论)

弦场论

M理论

参考出处

Greene, Brian. The Elegant Universe （台湾中文译本《优雅的宇宙》或大陆中文译本《宇宙的琴弦》）. W.W. Norton and Co. New York,NY. c1999. ISBN 978-0-375-70811-4

Witten, E. ,

Hull, C. - Townsend, P ,

Smolin Lee. (简体中文译本)，ISBN 978-7-5357-5240-6

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。