克莱罗定理
内容克莱罗假设地球是由密度不同的均匀物质层圈组成的椭球体,各椭球面都是重力等位面,且各层密度由地心向外有规律的减小。椭球面上纬度为φ一点的重力加速度g为:g=G[1+(52m−−-->f)sin2-->ϕϕ-->],{\displaystyleg=G\left[1+\left({\frac{5}{2}}m-f\right)\sin^{2}\phi\right]\,}赤道中G为地球赤道上的重力加速度,m为为赤道上的离心力与赤道上的重力加速度之比,f为地球椭球扁率。参考文献孔祥元郭际明刘宗泉.大地测量学基础(M)1.武汉:武汉大学出版社.2005.ISBN978-7-307-04837-9.
内容
克莱罗假设地球是由密度不同的均匀物质层圈组成的椭球体,各椭球面都是重力等位面,且各层密度由地心向外有规律的减小。椭球面上纬度为 φ 一点的重力加速度g 为: g = G [ 1 + ( 5 2 m − − --> f ) sin 2 --> ϕ ϕ --> ] , {\displaystyle g=G\left[1+\left({\frac {5}{2}}m-f\right)\sin ^{2}\phi \right]\ ,} 赤道中 G 为地球赤道上的重力加速度,m 为为赤道上的离心力与赤道上的重力加速度之比,f 为地球椭球扁率。
参考文献
孔祥元 郭际明 刘宗泉. 大地测量学基础 (M) 1. 武汉: 武汉大学出版社. 2005. ISBN 978-7-307-04837-9.
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。
文章来源:内容词条
——— 没有了 ———
编辑:阿族小谱

文章价值打分
- 有价值
- 一般般
- 没价值
当前文章打 0 分,共有 0 人打分
文章观点支持

0

0
文章很值,打赏犒劳一下作者~



打赏作者
“感谢您的打赏,我会更努力的创作”
— 请选择您要打赏的金额 —
{{item.label}}


{{item.label}}

打赏成功!
“感谢您的打赏,我会更努力的创作”
返回
打赏
私信
24小时热门
推荐阅读
· 黎曼-罗赫定理
一些数据我们从一个亏格g的连通紧黎曼曲面开始,在上面取定一点P。我们想知道极点只在P的函数。这是向量空间的一个递增序列:没有极点的函数(即常值函数),在P有单极点,在P点最多有两个极点,三个极点……这些空间都是有限维的。在g=0我们可知维数的序列前几项为这可由部分分式理论得出。反之,如果此序列开始为则g必然是零(所谓黎曼球面)。由椭圆函数理论知,g=1时此序列是且这也刻画了g=1情形。当g>2时,序列前端不是固定的;但我们可以确定此序列的后端。我们也可以看到为什么g=2的情形是特殊的,由超椭圆曲线理论,其序列开始几项为这些结论为何具有这种形式可以追溯到此定理的表述(罗赫的部分):两个维数之差。当其中一个可以为零,我们得到一个确定的公式,对亏格与度数(即自由度的个数)是线性的。这些例子已经可重构出如下形式对g=1,修正项当度数为0时是1;其它情形是0。整个定理说明修正项是函数空间的一个“补空...
· 弗罗贝尼乌斯定理
参见微分系统的可积性条件参考RalphAbrahamandJerroldE.Marsden,FoundationsofMechanics,(1978)Benjamin-Cummings,LondonISBN0-8053-0102-XSeetheorem2.2.26.
· 亚历克西斯·克劳德·克莱罗
生平克莱罗出生于法国首都巴黎,父亲是一位数学教师。克莱罗很小就显示了数学方面的天赋,在其父亲的指导下,克莱罗12岁就写了一篇有关四次曲线的论文。16岁时又完成了《关于双重曲率曲线的研究》(Recherchessurlescourbesadoublecourbure)一书(此书于1731年出版),这部著作得到了法国科学院的重视,因此克莱罗18岁时就被破格选为法国科学院院士。1736年,克莱罗跟随皮埃尔·莫佩尔蒂所率领的探险队前往北欧拉普兰进行子午线长度测量,此次结果证明了地球是扁球形。从北欧归来后,克莱罗于1743年发表了《关于地球形状的理论》(Théoriedelafiguredelaterre),在这部著作中首次阐述了地球几何扁率与重力扁率的关系,即著名的克莱罗定理。该定理为为利用重力资料研究地球形状奠定了基础。专注于天文上的运动他得到解出三体问题近似解的巧妙方法;在1750年,他以一篇...
· 定理
各种数学叙述(按重要性来排列)引理(又称辅助定理,补理)-某个定理的证明的一部分的叙述。它并非主要的结果。引理的证明有时还比定理长,例如舒尔引理。推论-一个从定理随之而即时出现的叙述。若命题B可以很快、简单地推导出命题A,命题A为命题B的推论。命题定理数学原理结构定理一般都有许多条件。然后有结论——一个在条件下成立的数学叙述。通常写作“若条件,则结论”。用符号逻辑来写就是条件→结论。而当中的证明不视为定理的成分。逆定理若存在某叙述为A→B,其逆叙述就是B→A。逆叙述成立的情况是A←→B,否则通常都是倒果为因,不合常理。若果叙述是定理,其成立的逆叙述就是逆定理。若某叙述和其逆叙述都为真,条件必要且充足。若某叙述为真,其逆叙述为假,条件充足。若某叙述为假,其逆叙述为真,条件必要。逻辑中的定理命题集合的可计算性问题(Calculabilite)我们可以通过可计算性(Calculabilite)这...
· 采样定理
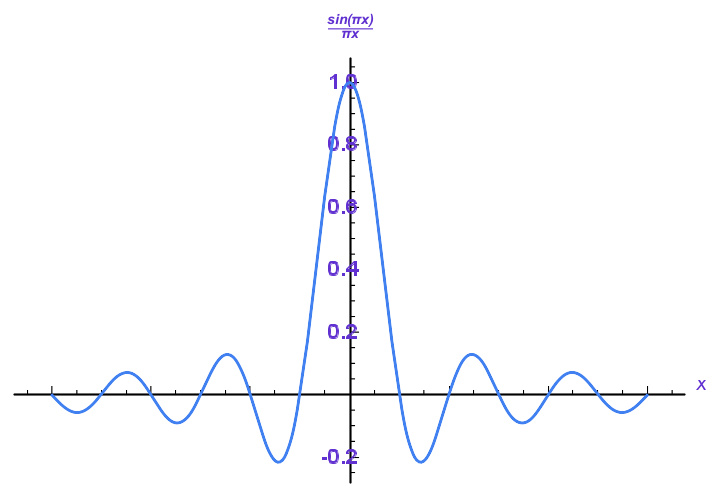
简介采样是将一个信号(例如时间或空间上连续的函数)转换为数字序列(时间或空间上离散的函数)的过程。这个定理的香农版本陈述为:如果函数x(t)不包含高于Bcps(次/秒)的频率,它完全取决于一系列相隔1/(2B)秒的点的纵坐标。因此2B样本/秒或更高的采样频率就足够了。相反,对于一个给定的采样频率fs,完全重构的频带限制为B≤fs/2。在频带限制过高(或根本没有频带限制)的情形下,重构表现出的缺陷称为混叠。现在对于此定义的陈述有时会很小心的指出x(t)必须不包括频率恰好为B的正弦曲线,或是B必须小于½的采样频率。这二个门槛,2B及fs/2会称为奈奎斯特速率(英语:Nyquistrate)及奈奎斯特频率。这些是x(t)及采样设备的属性。上述的不等式会称为奈奎斯特准则,有时会称为拉贝准则(Raabecondition)。此定理也可以用在其他定义域(例如离散系统)的函数下,唯一的不同是量测t,fs...
知识互答
关于我们

关注族谱网 微信公众号,每日及时查看相关推荐,订阅互动等。
APP下载

下载族谱APP 微信公众号,每日及时查看

扫一扫添加客服微信






















{{item.time}} {{item.replyListShow ? '收起' : '展开'}}评论 {{curReplyId == item.id ? '取消回复' : '回复'}}