庞加莱度量-族谱新闻-族谱网

庞加莱度量

2020-10-16

出处：族谱网

作者：阿族小谱

浏览:1329次

转发:0次

评论:0

黎曼曲面上的度量概要复平面上的度量可写成一般形式这里λ是z与z¯¯-->{displaystyle{overline{z}}}的一个实正函数。复平面上曲线γ的长度为复平面

黎曼曲面上的度量概要

复平面上的度量可写成一般形式

这里 λ 是 z 与 z¯ ¯ -->{\displaystyle {\overline {z}}} 的一个实正函数。复平面上曲线 γ 的长度为

复平面上子集 M 之面积是

这里 ∧ ∧ -->{\displaystyle \wedge } 是用于构造体积形式的外积。度量的行列式等于 λ λ -->4{\displaystyle \lambda ^{4}}，故而行列式的平方根是 λ λ -->2{\displaystyle \lambda ^{欧几里得复平面上的欧几里得体积形式为 dx∧ ∧ -->dy{\displaystyle dx\wedge dy}，从而我们有

函数 Φ Φ -->(z,z¯ ¯ -->){\displaystyle \Phi (z,{\overline {z}})} 称为度量的势能（potential of the metric），如果

拉普拉斯–贝尔特拉米算子为

度量的高斯曲率由

给出，这个曲率是里奇数量曲率的一半。

等距保持角度与弧长。在黎曼曲面上，等距与坐标变换等价：即拉普拉斯-贝尔特拉米算子与曲率在等距下不变。从而，比如设 S 是一个黎曼曲面带有度量 λ λ -->2(z,z¯ ¯ -->)dzdz¯ ¯ -->{\displaystyle \lambda ^{2}(z,{\overline {z}})\,dzd{\overline {z}}} 而 T 是带有度量 μ μ -->2(w,w¯ ¯ -->)dwdw¯ ¯ -->{\displaystyle \mu ^{2}(w,{\overline {w}})\,dw\,d{\overline {w}}} 的黎曼曲面，则映射

以及 f=w(z){\displaystyle f=w(z)} 是等距当且仅当它是共形的以及

在这里，映射为共形的也就是条件

即

庞加莱平面上的度量与体积元

庞加莱半平面模型中上半平面 H 的庞加莱度量张量为

这里我们记 dz=dx+idy{\displaystyle dz=dx+i\,dy}。这个度量张量在SL(2,R)的作用下不变。这就是，如果我们记

对 ad− − -->bc=1{\displaystyle ad-bc=1}，则我们可算得

与

无穷小变换为

从而

这样便清楚地表明度量张量在 SL(2,R) 的作用下不变。

不变体积元素为

对 z1,z2∈ ∈ -->H{\displaystyle z_{1},z_{2}\in \mathbb {H} } 度量为

度量的另一个有用的形式是用交比给出。给定紧化复平面C^ ^ -->=C∪ ∪ -->∞ ∞ -->{\displaystyle {\hat {\mathbb {C} }}=\mathbb {C} \cup \infty } 上任意四点 z1,z2,z3{\displaystyle z_{1},z_{2},z_{3}} 与z4{\displaystyle z_{4}}，交比定义为

那么度量用交比表示为

这里 z1× × -->{\displaystyle z_{1}^{\times }} 与 z2× × -->{\displaystyle z_{2}^{\times }} 是端点，位于实数轴上，测地线连接 z1{\displaystyle z_{1}} 与 z2{\displaystyle z_{2}}。这些点是有顺序的故 z1{\displaystyle z_{1}} 位于 z1× × -->{\displaystyle z_{1}^{\times }} 与 z2{\displaystyle z_{2}} 之间。

这个度量张量的测地线是在两个端点处垂直于实轴的圆弧（的一段），即端点位于实轴的上半圆周。

从平面到圆盘的共形映射

上半平面可以共形地映到单位圆盘，用莫比乌斯变换

这里单位圆盘上的点 w 对应于上半平面上的点 z。在这个映射中，常数 z0 可取上半平面上任何一点；这个点将映为圆盘的中心。实数轴 ℑ ℑ -->z=0{\displaystyle \Im z=0} 映为单位圆盘的边界 |w|=1{\displaystyle |w|=1}。实常数 ϕ ϕ -->{\displaystyle \phi } 将圆盘旋转任意一个角度。

典范映射是

将 i 映为圆盘的中心，0 映为圆盘的最低点。

庞加莱圆盘上的度量与体积元素

庞加莱圆盘模型里的庞加莱度量张量在单位圆盘U={z=x+iy:|z|=(x2+y2)≤ ≤ -->1}{\displaystyle U=\{z=x+iy:|z|={\sqrt {(x^{2}+y^{2})}}\leq 1\}} 上为

体积形式为

对 z1,z2∈ ∈ -->U{\displaystyle z_{1},z_{2}\in U} 的庞加莱度量为

这个度量张量的测地线是在端点处正交于圆盘边界的圆弧。

穿孔圆盘模型

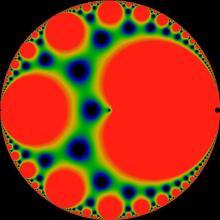
穿孔圆盘坐标上的 J-不变量（J-invariant）；这是 nome 的一个函数。

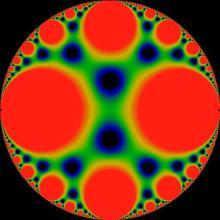
庞加莱圆盘坐标上的 J-不变量；注意这个圆盘比文中给出的典范坐标旋转了90度。

第二个将上半平面映成圆盘是 q-映射：

这里 q 是 nome（Nome），τ τ -->{\displaystyle \tau } 是半周期比例（half-period ratio）。在上一节的记号中，τ τ -->{\displaystyle \tau } 是上半平面 ℑ ℑ -->τ τ -->>0{\displaystyle \Im \tau >0} 的坐标。这个映射映到穿孔圆盘，因为值 q=0 不在映射的像中。

上半平面的庞加莱度量在 q-圆盘上诱导一个度量

度量的势能是

施瓦茨引理

庞加莱度量在调和函数上距离减小。这是施瓦茨引理的一个推广，称为施瓦茨-阿尔福斯-皮克定理（Schwarz-Alhfors-Pick theorem）。

另见

富克斯群（Fuchsian group）

富克斯模型（Fuchsian model）

克莱因群

克莱因模型

庞加莱圆盘模型

庞加莱半平面模型

本原测地线（Prime geodesic）