历史

1951年，霍夫曼和他在MIT信息论的同学得选择是完成学期报告还是期末考试。导师罗伯特·法诺出的学期报告题目是，查找最有效的二进制编码。由于无法证明哪个已有编码是最有效的，霍夫曼放弃对已有编码的研究，转向新的探索，最终发现了基于有序频率二叉树编码的想法，并很快证明了这个方法是最有效的。霍夫曼使用自底向上的方法构建二叉树，避免了次优算法香农-范诺编码的最大弊端──自顶向下构建树。

1952年，于论文《一种构建极小多余编码的方法》（ A Method for the Construction of Minimum-Redundancy Codes ）中发表了这个编码方法。

问题定义与解法

Fig.1

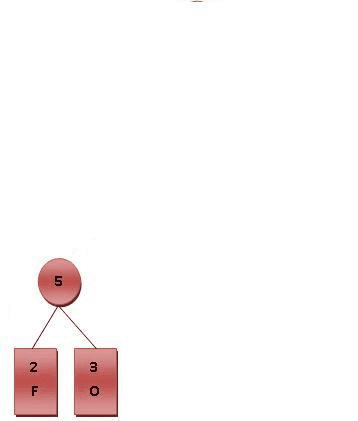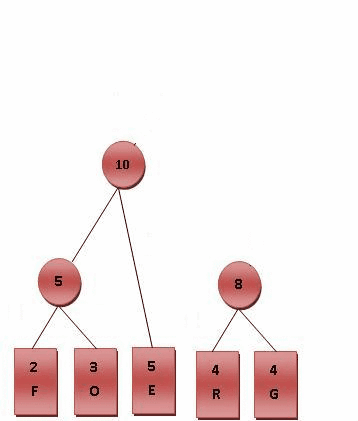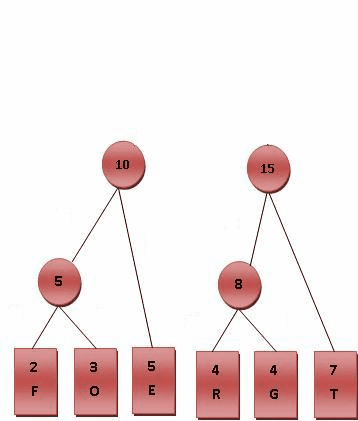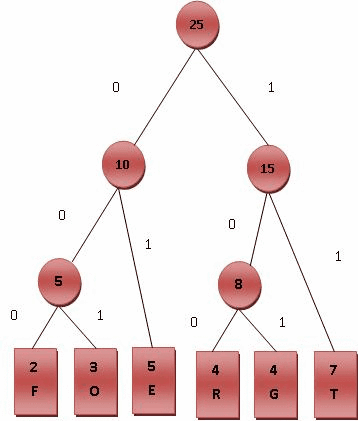
Fig.2 霍夫曼编码演算步骤, 左右树排列顺序可以加限制或不加限制

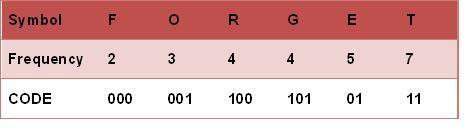
Fig.3

广义

给定

欲知

狭义

输入

输出

目标

示例

霍夫曼树常处理符号编写工作。根据整组数据中符号出现的频率高低，决定如何给符号编码。如果符号出现的频率越高，则给符号的码越短，相反符号的号码越长。假设我们要给一个英文单字 "F O R G E T" 进行霍夫曼编码，而每个英文字母出现的频率分别列在 Fig.1 。

演算过程

（一）进行霍夫曼编码前，我们先创建一个霍夫曼树。

最后产生的树状图就是霍夫曼树，参考 Fig.2 。 （二）进行编码

实现方法

数据压缩

实现霍夫曼编码的方式主要是创建一个二叉树和其节点。这些树的节点可以存储在数组里，数组的大小为符号（symbols）数的大小 n ，而节点分别是终端节点（叶节点）与非终端节点（内部节点）。

一开始，所有的节点都是终端节点，节点内有三个字段：

1.符号（Symbol）

2.权重（Weight、Probabilities、Frequency）

3.指向父节点的链接（Link to its parent node）

而非终端节点内有四个字段：

1.权重（Weight、Probabilities、Frequency）

2.指向两个子节点的链接（Links to two child node）

3.指向父节点的链接（Link to its parent node）

基本上，我们用"0"与"1"分别代表指向左子节点与右子节点，最后为完成的二叉树共有 n 个终端节点与 n-1 个非终端节点，去除了不必要的符号并产生最佳的编码长度。

过程中，每个终端节点都包含着一个权重（Weight、Probabilities、Frequency），两两终端节点结合会产生一个新节点， 新节点的权重 是由 两个权重最小的终端节点权重之总和 ，并持续进行此过程直到只剩下一个节点为止。

实现霍夫曼树的方式有很多种，可以使用优先队列（Priority Queue）简单达成这个过程，给与权重较低的符号较高的优先级（Priority），算法如下：

⒈把n个终端节点加入优先队列，则n个节点都有一个优先权Pi，1 ≤ i ≤ n

⒉如果队列内的节点数>1，则：

⒊最后在优先队列里的点为树的根节点（root）

而此算法的时间复杂度（Time Complexity）为O（ n log n ）；因为有n个终端节点，所以树总共有2n-1个节点，使用优先队列每个循环须O（log n ）。

此外，有一个更快的方式使时间复杂度降至线性时间（Linear Time）O（ n ），就是使用两个队列（Queue）创件霍夫曼树。第一个队列用来存储n个符号（即n个终端节点）的权重，第二个队列用来存储两两权重的合（即非终端节点）。此法可保证第二个队列的前端（Front）权重永远都是最小值，且方法如下：

⒈把n个终端节点加入第一个队列（依照权重大小排列，最小在前端）

⒉如果队列内的节点数>1，则：

⒊最后在第一个队列的节点为根节点

虽然使用此方法比使用优先队列的时间复杂度还低，但是注意此法的第1项，节点必须依照权重大小加入队列中，如果节点加入顺序不按大小，则需要经过排序，则至少花了O（ n log n ）的时间复杂度计算。

但是在不同的状况考量下，时间复杂度并非是最重要的，如果我们今天考虑英文字母的出现频率，变量n就是英文字母的26个字母，则使用哪一种算法时间复杂度都不会影响很大，因为n不是一笔庞大的数字。

数据解压缩

简单来说，霍夫曼码树的解压缩就是将得到的前置码（Prefix Huffman code）转换回符号，通常借由树的追踪（Traversal），将接收到的比特串（Bits stream）一步一步还原。但是要追踪树之前，必须要先重建霍夫曼树 ；某些情况下，如果每个符号的权重可以被事先预测，那么霍夫曼树就可以预先重建，并且存储并重复使用，否则，发送端必须预先发送霍夫曼树的相关信息给接收端。

最简单的方式，就是预先统计各符号的权重并加入至压缩之比特串，但是此法的运算量花费相当大，并不适合实际的应用。若是使用Canonical encoding，则可精准得知树重建的数据量只占 B 2^ B 比特（其中B为每个符号的比特数（bits））。如果简单将接收到的比特串一个比特一个比特的重建，例如："0"表示父节点，"1"表示终端节点，若每次读取到1时，下8个比特则会被解读是终端节点（假设数据为8-bit字母），则霍夫曼树则可被重建，以此方法，数据量的大小可能为2~320字节不等。虽然还有很多方法可以重建霍夫曼树，但因为压缩的数据串包含"traling bits"，所以还原时一定要考虑何时停止，不要还原到错误的值，如在数据压缩时时加上每笔数据的长度等。

数据长度

设符号集合 S = { s 1 , s 2 , ⋯ ⋯ --> , s n } {\displaystyle S=\left\{s_{1},s_{2},\cdots ,s_{n}\right\}} ， P ( s j ) {\displaystyle P\left(s_{j}\right)} 为 s j {\displaystyle s_{j}} 发生的概率 ， L ( s j ) {\displaystyle L\left(s_{j}\right)} 为 s j {\displaystyle s_{j}} 编码的长度

熵（Entropy）

霍夫曼码平均长度

霍夫曼码的长度

霍夫曼码的平均编码长度： 设 b = m e a n ( L ) N {\displaystyle b=mean\left(L\right)N} ， N {\displaystyle N} 为数据长度

示范程序

//以下為C++程式碼，在GCC下編譯通過//僅用於示範如何根據權值建構霍夫曼樹，//沒有經過性能上的優化及加上完善的異常處理。#include#include#include#includeusingnamespacestd;constintsize=10;structnode//霍夫曼樹節點結構{unsignedkey;//保存權值node*lchild;//左孩子指針node*rchild;//右孩子指針};dequeforest;dequecode;//此處也可使用bitsetnode*ptr;intfrequency[size]={0};voidprintCode(dequeptr);//用於輸出霍夫曼編碼boolcompare(node*a,node*b){returna->keykey;}intmain(intargc,char*argv[]){for(inti=0;i>frequency[i];//輸入10個權值ptr=newnode;ptr->key=frequency[i];ptr->lchild=NULL;ptr->rchild=NULL;forest.push_back(ptr);}//形成森林，森林中的每一棵樹都是一個節點//從森林構建霍夫曼樹for(inti=0;ikey=forest[0]->key+forest[1]->key;ptr->lchild=forest[0];ptr->rchild=forest[1];forest.pop_front();forest.pop_front();forest.push_back(ptr);}ptr=forest.front();//ptr是一個指向根的指針system("PAUSE");returnEXIT_SUCCESS;}voidprintCode(dequeptr){//dequefor(inti=0;i<ptr.size();i++){if(ptr[i])cout<<"1";elsecout<<"0";}}

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。