简述

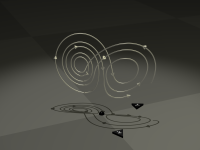
洛伦茨方程的一条轨迹被描绘成金属线，以展现方向以及三维结构

洛伦茨吸引子及其导出的方程组是由爱德华·诺顿·洛伦茨于1963年发表，最初是发表在《大气科学杂志》（ Journal of the Atmospheric Sciences ）杂志的论文《 Deterministic Nonperiodic Flow 》中提出的，是由大气方程现的对流卷方程简化得到的。

这一洛伦茨模型不只对非线性数学有重要性，对于气候和天气预报来说也有着重要的含义。行星和恒星大气可能会表现出多种不同的准周期状态，这些准周期状态虽然是完全确定的，但却容易发生突变，看起来似乎是随机变化的，而模型对此现象有明确的表述。

从技术角度看来，洛伦茨振子具有非线性、三维性和确定性。2001年，沃里克·塔克尔（Warwick Tucker）证明出在一组确定的参数下，系统会表现出混沌行为，显示出人们今天所知的奇异吸引子。这样的奇异吸引子是豪斯多夫维数在2与3之间的分形。彼得·格拉斯伯格（Peter Grassberger）已于1983年估算出豪斯多夫维数为2.06 ± 0.01，而 关联维数 （ 英语 ： correlation dimension ） 为2.05 ± 0.01。

此系统也会出现在单模激光 和发电机 的简化模型中。除此之外，闭环对流、水轮转动等物理模型也有此系统的应用。

洛伦茨方程

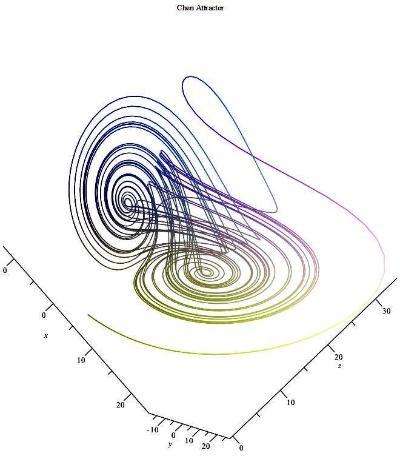
标出刻度的轨迹

洛伦茨方程是基于纳维－斯托克斯方程、热传导方程和连续性方程简化得出，最初的形式为：

v → → --> {\displaystyle {\vec {v}}} ——流速， T {\displaystyle T} ——流体温度， T 0 {\displaystyle T_{0}} ——上限温度（也可以写成 T 0 + Δ Δ --> T {\displaystyle T_{0}+\Delta T} ）， ρ ρ --> {\displaystyle \rho } ——密度， p {\displaystyle p} ——压强， g → → --> {\displaystyle {\vec {g}}} ——引力， γ γ --> {\displaystyle \gamma } 、 χ χ --> {\displaystyle \chi } 、 ν ν --> {\displaystyle \nu } ——依次为热膨胀系数、热扩散率和动黏滞系数。

简化后的形式称为 洛伦茨方程 ，是决定洛伦茨振子状态的方程为一组常微分方程：

含时间参数的形式：

σ σ --> {\displaystyle \sigma } 称为 普兰特尔数 ， ρ ρ --> {\displaystyle \rho } 称为 瑞利数 。所有的 σ σ --> {\displaystyle \sigma } ， ρ ρ --> {\displaystyle \rho } ， β β --> {\displaystyle \beta } > 0，但通常 σ σ --> {\displaystyle \sigma } = 10， β β --> {\displaystyle \beta } = 8/3， ρ ρ --> {\displaystyle \rho } 不定。若 ρ ρ --> < 1 {\displaystyle \rho <1} ，则吸引子为原点，没阻尼何其他稳定点。1≤ρ b ( ρ ρ --> − − --> 1 ) {\displaystyle ~x=\pm {\sqrt {b(\rho -1)}}} 、 y = ± ± --> b ( ρ ρ --> − − --> 1 ) {\displaystyle ~y=\pm {\sqrt {b(\rho -1)}}} 、 z = ρ ρ --> − − --> 1 {\displaystyle ~z=\rho -1} 。系统在 ρ ρ --> {\displaystyle \rho } = 28时表现出混沌特性，但 ρ ρ --> {\displaystyle \rho } 为其他值时会显示出具纽结的周期轨道。例如，当 ρ ρ --> = 99.96 {\displaystyle \rho =99.96} 时，图像变为一个 T (3,2)环面纽结。

瑞利数

源代码

GNU Octave

下面是GNU Octave模拟洛伦茨吸引子的源代码：

Borland C

#include#includevoidmain(){doublex=3.051522,y=1.582542,z=15.62388,x1,y1,z1;doubledt=0.0001;inta=5,b=15,c=1;intgd=DETECT,gm;initgraph(&gd,&gm,"C:\\BORLANDC\\BGI");do{x1=x+a*(-x+y)*dt;y1=y+(b*x-y-z*x)*dt;z1=z+(-c*z+x*y)*dt;x=x1;y=y1;z=z1;putpixel((int)(19.3*(y-x*0.292893)+320),(int)(-11*(z+x*0.292893)+392),9);}while(!kbhit());closegraph();}

Borland Pascal

ProgramLorenz;UsesCRT,Graph;Constx:Real=3.051522;y:Real=1.582542;z:Real=15.62388;dt=0.0001;a=5;b=15;c=1;Vargd,gm:Integer;x1,y1,z1:Real;Begingd:=Detect;InitGraph(gd,gm,"c:\bp\bgi");WhilenotKeyPressedDoBeginx1:=x+a*(-x+y)*dt;y1:=y+(b*x-y-z*x)*dt;z1:=z+(-c*z+x*y)*dt;x:=x1;y:=y1;z:=z1;PutPixel(Round(19.3*(y-x*0.292893)+320),Round(-11*(z+x*0.292893)+392),9);End;CloseGraph;ReadKey;End.

Fortran

program LorenzSystemreal,parameter::sigma=10real,parameter::r=28real,parameter::b=2.666666real,parameter::dt=.01integer,parameter::n=1000real x,y,zopen(1,file="result.txt",form="formatted",status="replace",action="write")x=10.;y=10.;z=10.do i=1,n,1x1=x+sigma*(y-x)*dty1=y+(r*x-x*z-y)*dtz1=z+(x*y-b*z)*dtx=x1y=y1z=z1write(1,*)x,y,zenddoprint*,"Done"close(1)end program LorenzSystem

QBASIC/FreeBASIC("fbc -lang qb")

DIMx,y,z,dt,x1,y1,z1ASSINGLEDIMa,b,cASINTEGERx=3.051522:y=1.582542:z=15.62388:dt=0.0001a=5:b=15:c=1SCREEN12PRINT"Press Esc to quit"WHILEINKEY$CHR$(27)x1=x+a*(-x+y)*dty1=y+(b*x-y-z*x)*dtz1=z+(-c*z+x*y)*dtx=x1y=y1z=z1PSET((19.3*(y-x*.292893)+300),(-11*(z+x*.292893)+360)),9WENDEND

参见

混沌映射列表

Takens定理

曼德布洛特集合

参考文献

（英文） Jonas Bergman, Knots in the Lorentz Equation , 学士毕业论文, Uppsala University 2004.

（英文） Frøyland, J., Alfsen, K. H. Lyapunov-exponent spectra for the Lorenz model. Phys. Rev. A. 1984, 29 : 2928–2931. doi:10.1103/PhysRevA.29.2928 .

（英文） P. Grassberger and I. Procaccia.Measuring the strangeness of strange attractors. Physica D. 1983, 9 : 189–208. doi:10.1016/0167-2789(83)90298-1 .

（英文） Lorenz, E. N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20 : 130–141. doi:10.1175/1520-0469(1963)0202.0.CO;2 .

（英文） Strogatz, Steven H. Nonlinear Systems and Chaos. Perseus publishing. 1994.

（英文） Tucker, W.A Rigorous ODE Solver and Smale"s 14th Problem. Found. Comp. Math. 2002, 2 : 53–117.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。