延伸阅读Chomet,S.(Ed.),D.N.A.GenesisofaDiscovery,1994,Newman-HemispherePress,London;NBafewcopiesareavailablefromNewman-Hemisphereat101SwanCourt,LondonSW35RY(phone:07092060530).Wilkins,Maurice,TheThirdManoftheDoubleHelix:TheAutobiographyofMauriceWilkinsISBN0-19-860665-6.Ridley,Matt;"FrancisCrick:DiscovereroftheGeneticCode(EminentLives)"wasfirstpublishedinJune2006intheUSAandwillbethenintheUKSeptember200...

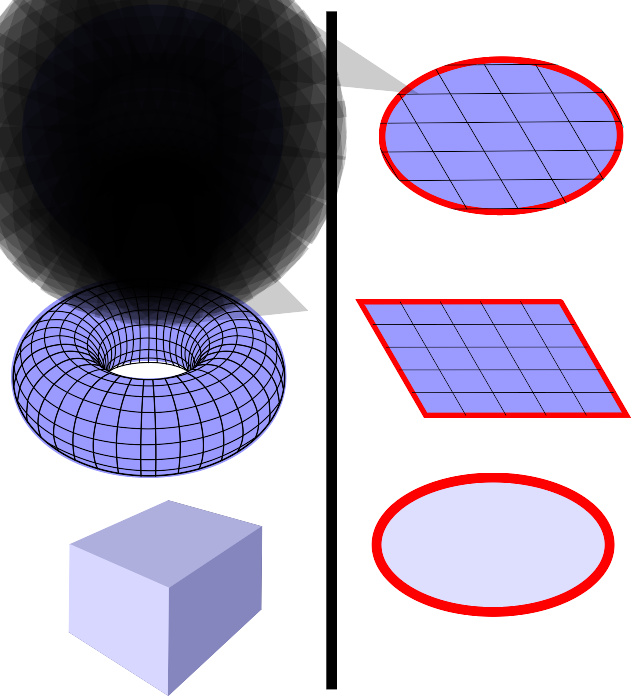
ℝ³ 上的斯托克斯公式设S是分片光滑的有向曲面，S的边界为有向闭曲线Γ，即ΓΓ-->=∂∂-->S{\displaystyle\Gamma=\partialS}，且Γ的正向与S的侧符合右手规则：函数P(x,y,z)、Q(x,y,z)、R(x,y,z)都是定义在“曲面S连同其边界Γ”上且都偏导数阶连续偏导数的函数，则有旋度定理可以用来计算穿过具有边界的曲面，例如，任何右边的曲面；旋度定理不可以用来计算穿过闭曲面的通量，例如，任何左边的曲面。在这图内，曲面以蓝色显示，边界以红色显示。这个公式叫做 ℝ³ 上的斯托克斯公式或开尔文－斯托克斯定理、旋度定理。这和函数的旋度有关，用梯度算符可写成：它将ℝ³ 空间上“向量场的旋度的曲面积分”跟“向量场在曲面边界上的线积分”之间建立联系，这是一般的斯托克斯公式（在 n=2 时）的特例，我们只需用ℝ³ 空间上的内积把向量场看作等价的1-形式。该定...

刚体若用在刚体运动时，位移这词语也可以包括刚体的旋转在内。对于这案例，刚体内部一个点（例如，质心、几何中心等等）的位移，称为线位移，而刚体的旋转则称为角位移。速度和距离位移矢量是粒子的新位置与旧位置的矢量差。这矢量差，除以所经过的时间，就是粒子的平均速度。粒子的瞬时速度则是位移矢量随着时间的导数。距离是一种标量，通常定义为位移矢量的大小（最小距离），或定义一条弯曲路径的长度（移动距离）。它不能给出运动方向。假设，从时间t=0{\displaystylet=0\,\!}开始，一个粒子的运动轨道为其中，t{\displaystylet\,\!}是时间，R{\displaystyle\mathbb{R}\,\!}是实数，Vn{\displaystyle\mathrm{V}^{n}\,\!}是n-维矢量空间。那么，粒子移动的瞬时速度v(t){\displaystyle\mathbf{v}(t)\,...

实验成果于1947年，兰姆以及罗伯特·雷瑟福（RobertRetherford）进行了一项实验，利用微波技术来刺激氢原子2S1/2{\displaystyle^{2}S_{1/2}}与2P1/2{\displaystyle^{2}P_{1/2}}能阶之间的射频跃迁（radio-frequencytransitions）。利用比光学跃迁（opticaltransitions）还要低的频率，使得多普勒谱线增宽（Dopplerbroadening）效应可以被忽略（因为多普勒谱线增宽跟频率呈正比关系）。他们两人发现如此使得2S1/2{\displaystyle^{2}S_{1/2}}能阶比2P1/2{\displaystyle^{2}P_{1/2}}能阶还高出约1000兆赫（MHz）的能量差。如此特殊的差异是量子电动力学中的单圈效应（one-loopeffect），可以解释为被原子发...

外部链接Stockton-on-TeesBoroughCouncil开放式目录计划中和蒂斯河畔斯托克顿相关的内容Stockton-on-Teesinthedevelopmentofthenorth-easterncoastHistoricaldataforStockton-on-TeesBBCTees–thelatestlocalnews,sport,entertainment,features,faith,travelandweather.