问题起源人们知道，区间的长度可以定义为端点值之差。若干个不交区间的并的长度应当是它们的长度之和。于是人们希望将长度的概念推广为比区间更复杂的集合。我们想构造一个映射m，它能将实数集的子集E映射为非负实数mE。称这样的映射（集函数）为集合E的测度。最理想的情况应该是m具有以下性质：mE对于实数集的所有子集E都有定义。对于一个区间I，mI应当等于其长度（端点数值之差）。如果{En}是一列不相交的集合，并且m在其上有定义，那么m(∪∪-->En)=∑∑-->mEn{\displaystylem(\cupE_{n})=\summE_{n}}。m具有平移不变性，即如果一个m有定义的集合E的每个元素都加一个相同的实数（定义为{x+y|x∈∈-->E}{\displaystyle\{x+y|x\inE\}}，记作E+y），那么m(E+y)=mE。遗憾的是，这样的映射（集函数）是不存在的。人们只能退而求其...

一、生平利昂·费斯廷格（LeonFestinger），美国著名社会心理学家，俄国犹太人后裔，通常称莱昂·费斯廷格、费斯汀格或费斯廷格。利昂·费斯廷格1.1早年1919年5月8日，利昂·费斯廷格出生在美国纽约布鲁克林一个俄国犹太人移民家庭。他父亲亚历克斯·费斯廷格（AlexxFestinger）是一位自学成才的刺绣制造商，母亲是萨拉·所罗门·费斯廷格。后来，利昂·费斯廷格就读于男子中学。1.2求学1939年，费斯廷格获得纽约市立学院理学士学位，大学毕业后，费斯廷格进入爱荷华大学，在社会心理学之父科特·勒温(KurtZadekLewin)的指导下，1940年获得心理学硕士学位，1942年获博士学位。科特·勒温试图建立心理学的“场论”（类似于物理学），以取代行为主义者的机械论模型。1.3任教同年，利昂·费斯廷格与女画家玛丽·奥利弗·Ballou结婚，两人生有3名子女：凯瑟琳、理查德和库尔特。之后...

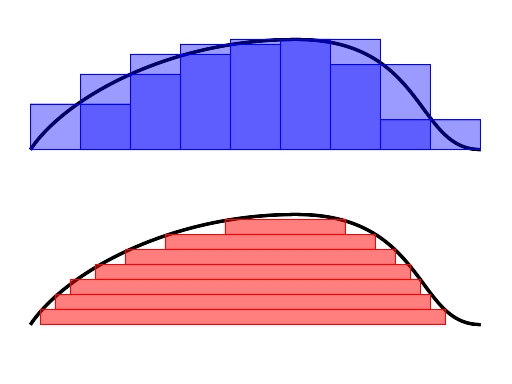
引入在闭区间a{\displaystylea}和b{\displaystyleb}之间对函数f{\displaystylef}的积分可以被看作是求f{\displaystylef}的函数图像下的面积。对于多项式这样比较常见的函数来说这个定义简而易懂。但是对于更加稀奇古怪的函数来说它是什么意思呢？广义地来说，对于什么样的函数“函数图像下的面积”这个概念有意义？这个问题的答案具有很大的理论性和实际性意义。19世纪里在数学中有把整个数学理论放到一个更加坚固的基础上的趋势。在这个过程中数学家也试图给积分计算提供一个稳固的定义。波恩哈德·黎曼提出的黎曼积分成功地为积分运算提供了一个这样的基础。黎曼积分的出发点是构造一系列容易计算的面积，这些面积最后收敛于给定的函数的积分。这个定义很成功，为许多其它问题提供了有用的答案。但是在求函数序列的极限的时候黎曼积分的效果不良，这使得这些极限过程难以分析。而这个...

辖区辖区地图利希滕贝格包括10个街区。参考文献

参考资料诺贝尔奖官方网站关于亨利·贝克勒生平介绍