历史

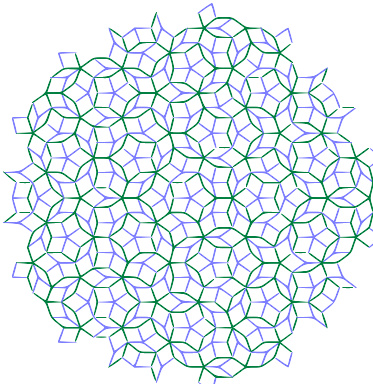
二维空间的彭罗斯拼图

准晶体的结构在20世纪之前就已经被建筑师熟知，例如在伊朗伊斯法罕的清真寺，上面瓷砖的图案就是按照准晶样式排列。

1961年，数学家王浩提出了用不同形状的拼图铺满平面的拼图问题。数学家们已经知道，可以用单一形状的拼图拼满一个平面，例如任意形状的四边形或者正六边形，但是当增加拼图单元的种类时，就能够构造出更多的拼满一个平面的方法。两年后，王浩的学生Robert Berger构造了一系列不具有周期性的拼图方法。之后铺满平面所需要的拼图种类越来越少，1976年罗杰·潘洛斯(Roger Penrose)构造了一系列只需要两种拼图的方法，这种方法拼出来的图案具有五次对称性。

之后丹尼尔·舍特曼发现了三维世界中的20面体准晶。这一准晶的拼图形式由两种不同的菱形组成。这篇文章发表于1984年，标题为“一种长程有序但是不具有平移对称性的金属相”（Metallic Phase with Long-Range Orientational Order and No Translational Symmetry）。他们发现的这一五次对称性结构产生于融化后快速冷却的Al-Mn合金中。

钬-镁-锌十二面体准晶

第二年Ishimasa等人报道了Ni-Cr颗粒中的十二次对称性。之后在V-Ni-Si和Cr-Ni-Si合金中又发现了八次对称衍射图。 多年以来已经发现了几百种具有多种组成和对称性的准晶体。最早发现的这种准晶体结构在热力学上是不稳定的，一旦加热就会重新变成规则晶体。但是1987年的时候发现了许多种稳定的准晶体，这样就可以合成更大的晶体用于进一步的结构及应用研究。

2009年，矿物学上的一个发现为准晶是否能在自然条件下形成提供了证据： 俄罗斯的一块铝锌铜矿上发现了Al 63 Cu 24 Fe 13 组成的准晶颗粒。和实验室中合成的一样，这些颗粒的结晶程度都非常好。

原理

一种典型的准晶体结构是三维空间的彭罗斯拼图（Penrose）。二维空间的彭罗斯拼图由内角为36度、144度和72度、108度的两种菱形组成，能够无缝隙无交叠地排满二维平面。这种拼图没有平移对称性，但是具有长程的有序结构，并且具有晶体所不允许的五次旋转对称性。

准晶体是其中原子的排列存在5次和6次以上对称轴的一种特殊的晶体。它既不同于非晶体，也不同于真正完整的晶体。晶体为具有平移对称的固体，即整个晶体中原子的排列都是很规则。三维晶体不可能具有5次和6次以上的对称轴，此点可由晶体学限制定理证明。而准晶体是无平移对称性但长程有序的固体，即在大范围内原子的排列是规则（有序）的，因此其电子衍射图仍具有明锐衍射斑。

参见

晶体

晶体结构

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。