玻尔模型的提出

20世纪初期，德国物理学家普朗克为解释黑体辐射现象，提出了量子论，揭开了量子物理学的序幕。19世纪末，瑞士数学教师巴耳末将氢原子的谱线表示成巴耳末公式，瑞典物理学家里德伯总结出更为普遍的光谱线公式里德伯公式：

其中 λ λ --> {\displaystyle {\lambda }} 为氢原子光谱波长，R为里德伯常数。

然而巴耳末公式和式里德伯公式都是经验公式，人们并不了解它们的物理含义。

1911年，英国物理学家卢瑟福根据1910年进行的α粒子散射实验，提出了原子结构的行星模型。在这个模型里，电子像太阳系的行星围绕太阳转一样围绕着原子核旋转。但是根据经典电磁理论，这样的电子会发射出电磁辐射，损失能量，以至瞬间坍缩到原子核里。这与实际情况不符，卢瑟福无法解释这个矛盾。

1912年，正在英国曼彻斯特大学工作的玻尔将一份被后人称作《卢瑟福备忘录》的论文提纲提交给他的导师卢瑟福。在这份提纲中，玻尔在行星模型的基础上引入了普朗克的量子概念，认为原子中的电子处在一系列分立的稳态上。回到丹麦后玻尔急于将这些思想整理成论文，可是进展不大。

1913年2月4日前后的某一天，玻尔的同事汉森拜访他，提到了1885年瑞士数学教师巴耳末的工作以及巴耳末公式，玻尔顿时受到启发。后来他回忆到“ 就在我看到巴耳末公式的那一瞬间，突然一切都清楚了， ”“ 就像是七巧板游戏中的最后一块。 ”这件事被称为玻尔的“二月转变”。

1913年7月、9月、11月，经由卢瑟福推荐，《哲学杂志》接连刊载了玻尔的三篇论文 ，标志着玻尔模型正式提出。这三篇论文成为物理学史上的经典，被称为玻尔模型的“三部曲”。

玻尔模型的主要内容

氢原子中的电子围绕原子核做圆周运动，运动的轨道是经典轨道。电子做圆周运动的向心力是由电子和原子核之间的库仑力提供的，即：

而电子的能量是动能加势能：

所以电子的轨道周期是：

因此电子的公转频率是：

而根据电磁学，电磁辐射频率是等于电子的公转频率。

但光谱中的辐射频率并不等于电子的公转频率，所以玻尔模型主要基于以下条件：

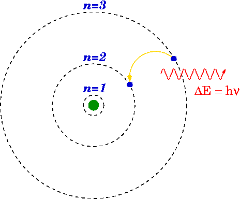
  玻尔模型的简单示意图。

定态条件

原子只能够稳定地存在于一系列的离散的能量状态之中，称为定态，原子要有任何能量的改变，都必须要在两个定态之间以跃迁的方式进行；所以电子只能处在一系列分立的定态上，并且不产生电磁辐射。

频率条件

当两个定态间的跃迁时，以电磁波的形式放出或吸收能量，其频率的值为 ν ν --> {\displaystyle \nu \,} 是唯一的并且有：

结合里德伯公式可以得到

代入电子能量的表达式可以得到电子运动的轨道半径：

结果

根据以上条件可以计算出，电子的能量：

其中α是精细结构常数，其大小约为1/137。 电子的轨道半径：

里德伯常数：

由玻尔模型可以计算出几个表征原子常用的物理量： 电子的第一轨道半径（n=1）：

通常用a 0 表示，称为 玻尔半径 。

电子在第一个轨道上运动的速度（n=1）：

称为玻尔第一速度，它表示电子在原子中的运动速度通常约为光速的1/137。

将氢原子的电子从基态移动到无限远处所需要的能量，即氢原子的电离能：

所以氢原子电子基态的能量约为-13.6eV。其余各态的能量为：

玻尔根据对应原理，结合里德伯公式提出了角动量量子化条件：

亦即是后期的玻尔-索末菲作用量量子条件的前身:

修正

英国光谱学家 亚弗列德·福勒 （ 英语 ： Alfred Fowler ） 质疑：应用玻尔模型计算出里德伯常数的数值 R = 109737.315 c m − − --> 1 {\displaystyle R=109737.315\,\mathrm {cm} ^{-1}} ；而实验值 R = 109677.58 c m − − --> 1 {\displaystyle R=109677.58\,\mathrm {cm} ^{-1}} ，二者相差大约万分之五。1914年，玻尔提出，这是因为原来的模型假设原子核静止不动而引起的。实际情况是，原子核的质量不是无穷大，它与电子绕共同的质心转动。玻尔对其理论进行了修正，用原子核和电子的折合质量 μ μ --> = m e M m e + M {\displaystyle \mu ={\frac {m_{e}M}{m_{e}+M}}} 代替了电子质量。这样的话，不同原子的里德伯常数R A 不同，

电子到质心的距离仍为原来理论中的第一轨道半径，与原子核的质量无关。

玻尔模型的实验验证

1897年，美国天文学家爱德华·皮克林在恒星弧矢增二十二的光谱中发现了一组独特的线系，称为皮克林线系。皮克林线系中有一些谱线靠近巴耳末线系，但又不完全重合，另外有一些谱线位于巴耳末线系两临近谱线之间。起初皮克林线系被认为是氢的谱线，然而玻尔提出皮克林线系是类氢离子He 发出的谱线。随后英国物理学家埃万斯在实验室中观察了He 的光谱，证实玻尔的判断完全正确。

和玻尔提出玻尔模型几乎同一时期，英国物理学家亨利·莫塞莱测定了多种元素的X射线标识谱线，发现它们具有确定的规律性，并得到了经验公式——莫塞莱定律。莫塞莱看到玻尔的论文，立刻发现这个经验公式可以由玻尔模型导出，为玻尔模型提供了有力的证据。

1914年，詹姆斯·弗兰克和古斯塔夫·赫兹进行了用电子轰击汞蒸汽的实验，即弗兰克-赫兹实验。实验结果显示，汞原子内确实存在能量为4.9eV的量子态。1920年代，弗兰克和赫兹又继续改进实验装置，发现了汞原子内部更多的量子态，有力地证实了玻尔模型的正确性。

1932年，哈罗德·尤里观察到了氢的同位素氘的光谱，测量到了氘的里德伯常数，和玻尔模型的预言符合得很好。

玻尔模型的推广

随着光谱实验水平的提高，人们发现了光谱具有精细结构。1896年，阿尔伯特·迈克耳孙和爱德华·莫雷观察到了氢光谱的H α 线是双线，随后又发现是三线。玻尔提出这可能是电子在椭圆轨道上做慢进动引起的。1916年索末菲在玻尔模型的基础上将圆轨道推广为椭圆形轨道，并且引入相对论修正，提出了索末菲模型。在考虑椭圆轨道和相对论修正后，索末菲计算出了H α 线的精细结构，与实验相符。然而进一步的研究发现，这样的解释纯属巧合。H α 线的精细结构有7条，必须彻底抛弃电子轨道的概念才能完全解释光谱的精细结构。

玻尔模型的困难

玻尔模型将经典力学的规律应用于微观的电子，不可避免地存在一系列困难。根据经典电动力学，做加速运动的电子会辐射出电磁波，致使能量不断损失，而玻尔模型无法解释为什么处于定态中的电子不发出电磁辐射。玻尔模型对跃迁的过程描写含糊。因此玻尔模型提出后并不被物理学界所欢迎，还遭到了包括卢瑟福、薛定谔在内的诸多物理学家的质疑。玻尔曾经的导师、剑桥大学的约瑟夫·汤姆孙拒绝对其发表评论。薛定谔甚至评价说是“糟透的跃迁” 。

此外，玻尔模型无法揭示氢原子光谱的强度和精细结构，也无法解释稍微复杂一些的氦原子的光谱，以及更复杂原子的光谱。因此，玻尔在领取1922年诺贝尔物理学奖时称：“这一理论还是十分初步的，许多基本问题还有待解决。”

玻尔模型引入了量子化的条件，但它仍然是一个“半经典半量子”的模型。完全解决原子光谱的问题必须彻底抛弃经典的轨道概念。尽管玻尔模型遇到了诸多困难，然而它显示出量子假说的生命力，为经典物理学矢量子物理学发展铺平了道路。

参阅

尼尔斯·玻尔

里德伯公式

惰性电子对效应可以用玻尔模型解释。

原子轨域

参考文献

^ Niels Bohr. On the Constitution of Atoms and Molecules . Phil.Mag. 26 (1913)1.

^ Niels Bohr. Systems Containing Only a Single Nucleus . Phil.Mag. 26 (1913)476.

^ Niels Bohr. Systems Containing Several Nuclei . Phil.Mag. 26 (1913)857.

^ W.Heisenberg. Physics & Beyond . Harper & Row Pub. (1972)75.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。