推导

德拜模型是普朗克黑体辐射定律的固态等价物，其中把电磁辐射视为盒中的光子气体。德拜模型把原子的振动视为盒中的声子（盒子就是固体）。大部分的计算步骤都是相同的。

考虑一个边长为 L {\displaystyle L} 的立方体。从盒中粒子一文可知，盒中的声波干扰的谐振模（现在只考虑与一个轴对齐的）具有波长：

其中 n {\displaystyle n} 是整数。一个声子的能量是：

其中 h {\displaystyle h} 是普朗克常数， ν ν --> n {\displaystyle \nu _{n}} 是声子的频率。我们估计频率与波长成反比，得出：

其中 c s {\displaystyle c_{s}} 是固体中的声速。在三维空间中，我们将使用：

频率与波长成反比的估计（意味着声速是恒定的）对于低能量声子是准确的，但对于高能量声子则不准确（参见声子）。这就是德拜模型的局限之一，对应于在中间的温度时结果的不准确，而在低温和高温时都是精确的。

现在来计算盒中的总能量：

其中 N ¯ ¯ --> ( E n ) {\displaystyle {\bar {N}}(E_{n})} 是盒中能量为 E n {\displaystyle E_{n}} 的声子数目。也就是说，总能量等于能量的和乘以具有该能量的声子的数目（在一维空间中）。在三维空间中，我们有：

现在，这就是德拜模型和普朗克黑体辐射定律不同的地方。与盒中的电磁辐射不一样，声子只有有限个能量状态，因为一个声子不能有无限的频率。它的频率由它的传播介质——固体的原子晶格所约束。考虑以下的横向声子的插图。

可以合理假设声子的最小波长是原子间距的两倍，如最下面的图所示。固体中有 N {\displaystyle N} 个原子。我们的固体是正方体，这意味着每一条边有 N 3 {\displaystyle {\sqrt[{3}]{N}}} 个原子。于是，原子间距为 L / N 3 {\displaystyle L/{\sqrt[{3}]{N}}} ，最小波长为：

使最大的模数 n {\displaystyle n} （对于光子是无限）为：

这是三重能量和的上极限：

对于缓慢变化的、表现良好的函数，求和可以用积分来代替（又称为托马斯-费米近似）：

到这里为止，还没有提到 N ¯ ¯ --> ( E ) {\displaystyle {\bar {N}}(E)} ，能量为 E {\displaystyle E\,} 的声子数目。声玻色从爱因斯坦因斯坦统计。它们的贡献由著名的玻色-爱因斯坦公式给出：

由于一个声子有三个可能的偏振态（一个纵向、两个横向，大致不影响它的能量），必须把以上的公式乘以3：

实际上我们使用了 有效声速 c s := c e f f {\displaystyle c_{s}:=c_{\rm {eff}}} ，也就是说，德拜温度 T d {\displaystyle T_{d}} （见下文）与 c e f f {\displaystyle c_{\rm {eff}}} 成正比，更加精确地 T D − − --> 3 ∝ ∝ --> c e f f − − --> 3 := ( 1 / 3 ) c l o n g − − --> 3 + ( 2 / 3 ) c t r a n s − − --> 3 {\displaystyle T_{D}^{-3}\propto c_{\rm {eff}}^{-3}:=(1/3)c_{\rm {long}}^{-3}+(2/3)c_{\rm {trans}}^{-3}} ，速度我们区分了纵向和横向的声波速度（贡献分别为1/3和2/3）。德拜温度或有效声速是晶体的硬度的一种衡量。

把此式代入能量积分，得：

这些积分之所以对于光子容易计算，是因为光的频率是无界的。如上面的图所示，这对于声子不成立。为了近似计算这个三重积分，德拜使用了球坐标系：

并大胆地用球的八分之一来近似代替立方体：

其中 R {\displaystyle R} 是球的半径，通过保持立方体和球的八分之一中的粒子数目相同来得出。立方体的体积是 N {\displaystyle N} 个单胞体积：

因此我们得到：

用球面上的积分来代替正确的积分，引入了模型的不准确性的另一个来源。

能量积分变为：

利用变量代换 x = h c s n 2 L k T {\displaystyle x={hc_{s}n \over 2LkT}} ：

为了把这个表达式简化，定义 德拜温度 T D {\displaystyle T_{D}} ——它的量纲与温度相同，因物质而异：

于是我们便得到比内能：

其中 D 3 ( x ) {\displaystyle D_{3}(x)} 是（第三）德拜函数。

对 T {\displaystyle T} 微分，我们便得到无量纲热容：

这个公式就是任何温度下德拜模型的结果。下面更基本的公式给出了低温和高温极限下的渐近表现。前面已经提到，这个表现是精确的，与中间温度的表现不同。低温时精确的根本原因，是由于德拜模型在低频率给出了精确的 色散关系 E ( ν ν --> ) {\displaystyle E(\nu )} ；高温时精确的原因，是由于对应于精确的 和规则 ( ∫ ∫ --> g ( ν ν --> ) d ν ν --> ≡ ≡ --> 3 N ) , {\displaystyle (\int g(\nu )\,{\rm {d\nu }}\equiv 3N)\,,} 关于每一个频率间隔中的振动数目。

德拜的推导

实际上，德拜用不同和更加简单的方法推出了这个方程。利用连续介质的固体力学，他发现频率小于某个特定值的振动状态的数目趋近于：

其中 V {\displaystyle V} 是体积， F {\displaystyle F} 是一个因子，他从弹性系数和密度计算。把这与温度T的量子谐振子的期望能量（已经由爱因斯坦在他的模型中使用）结合，便给出能量：

如果振动频率趋于无穷大。这个形式给出了 T 4 {\displaystyle T^{4}} 的表现，它在低温时是正确的。但德拜意识到N个原子不可能有超过 3 N {\displaystyle 3N} 个振动状态。他假设在原子固体中，振动状态的频谱将继续遵循以上的规则，到一个最大的频率 ν ν --> m {\displaystyle \nu _{m}} 为止，使得总的状态数目为 3 N {\displaystyle 3N} ：

德拜知道这个假设不是真正正确的（较高的频率比假设要更加密集），但它保证了高温时的正确表现（杜隆-珀蒂定律）。于是，能量由以下给出：

其中 T D {\displaystyle T_{D}} 是 h ν ν --> m / k {\displaystyle h\nu _{m}/k} 。

其中 D 3 {\displaystyle D_{3}} 是一个函数，后来命名为三阶德拜函数。

低温极限

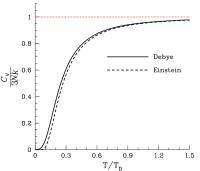
  比较德拜、爱因斯坦分别对于热容与温度之间关系的预测。

德拜固体的温度称为低的，如果 T ≪ ≪ --> T D {\displaystyle T\ll T_{D}} ，在这个情况下：

这个定积分可以精确计算：

在低温极限中，德拜模型的局限不适用，它给出了（声子）热容、温度、弹性系数，以及每个原子的体积（后面的数量是包含在德拜温度之中的）之间的正确关系。

高温极限

德拜固体的温度称为高的，如果 T ≫ ≫ --> T D {\displaystyle T\gg T_{D}} 。 e x − − --> 1 ≈ ≈ --> x {\displaystyle e^{x}-1\approx x} 如果 | x | << 1 {\displaystyle |x|<<1} ，得出：

这就是杜隆-珀蒂定律，它是相当准确的，虽然它没有考虑非谐性，这造成了热容进一步上升。如果固体是导体或半导体，那么它的总热容还可能含有电子的不可忽略的贡献。

参见

玻色气体

盒中气体

参考文献

CRC Handbook of Chemistry and Physics , 56th Edition (1975-1976)

Schroeder, Daniel V. An Introduction to Thermal Physics . Addison-Wesley, San Francisco, Calif. (2000). Section 7.5.

Kittel, Charles, Introduction to Solid State Physics , 7th Ed., Wiley, (1996)

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。