问题的提出

一笔画问题是柯尼斯堡问题经抽象化后的推广，是图遍历问题的一种。在柯尼斯堡问题中，如果将桥所连接的地区视为点，将每座桥视为一条边，那么问题将变成：对于一个有着四个顶点和七条边的连通图G(S,E){\displaystyle G(S,E)}，能否找到一个恰好包含了所有的边，并且没有重复的路径。欧拉将这个问题推广为：对于一个给定的连通图，怎样判断是否存在着一个恰好包含了所有的边，并且没有重复的路径？这就是一笔画问题。用图论的术语来说，就是判断这个图是否是一个能够遍历完所有的边而没有重复。这样的图现称为欧拉图。这时遍历的路径称作欧拉路径（一个环或者一条链），如果路径闭合（一个圈），则称为欧拉回路。

一笔画问题的推广是多笔画问题，即对于不能一笔画的图，探讨最少能用多少笔来画成。

一笔画定理

对于一笔画问题，有两个判断的准则，它们都由欧拉提出并证明。

定理一

连通的无向图 G{\displaystyle G} 有欧拉路径的充要条件是：G{\displaystyle G}中奇顶点（连接的边数量为奇数的顶点）的数目等于0或者2。

连通的无向图 G{\displaystyle G} 是欧拉环（存在欧拉回路）的充要条件是：G{\displaystyle G}中每个顶点的度都是偶数。。

证明：

连通无向图有欧拉路径的充要条件也可以写作“图中奇顶点数目不多于2个”，这是因为奇顶点数目不可能是1个。实际上，连通无向图中，奇顶点的数目总是偶数。

对于不连通的无向图，如果有两个互不连通的部分都包含至少一条边，那么显然不能一笔画。只有当此图的边全都在某一个连通部分中（即其它的连通部分都是一个个孤立的顶点，度数为0），并满足连通无向图关于一笔画的充要条件，而该图才能一笔画。也即是说，可以一笔画的（无向）图如果不是连通图，就必定是一个可以一笔画的连通图与若干个孤立顶点的组合。

除了用顶点的度数作为判定的充要条件，还可以用图中边的特性来作为欧拉回路存在的判定准则。连通的无向图 G{\displaystyle G}中存在欧拉回路，等价于图G{\displaystyle G}所有的边可以划分为若干个环的不交并。具体来说，等价于存在一系列的环C1,C2,⋯ ⋯ -->,Cm{\displaystyle C_{1},C_{2},\cdots ,C_{m}}，使得图G{\displaystyle G}里的每一条边都恰好属于某一个环。

定理二

如果连通无向图 G{\displaystyle G} 有 2k{\displaystyle 2k} 个奇顶点，那么它可以用 k{\displaystyle k} 笔画成，并且至少要用 k{\displaystyle k} 笔画成。

证明：将这 2k{\displaystyle 2k} 个奇顶点分成 k{\displaystyle k} 对后分别连起，则得到一个无奇顶点的连通图。由上知这个图是一个环，因此去掉新加的边后至多成为 k{\displaystyle k} 条欧拉路径，因此必然可以用 k{\displaystyle k} 笔画成。但是假设全图可以分为 q{\displaystyle q} 条欧拉路径，则由定理一知，每条链中只有不多于两个奇顶点，于是 2q≥ ≥ -->2k{\displaystyle 2q\geq 2k}。因此必定要 k{\displaystyle k} 笔画成。

有向图的一笔画

对有向图来说，一笔画不仅指遍历所有边，而且要遵循正确的方向。严谨地说，一个连通有向图G{\displaystyle G}有欧拉路径，指存在一个顶点，从它出发，沿着有向边的方向，可以不重复地遍历图中所有的边。有向图的欧拉回路则是指可以从某一顶点开始，沿有向边的方向不重复地遍历所有边，然后回到原来出发的顶点。用类似于定理一中证明的思路，可以得到有向图一笔画的判定准则：

一个连通的有向图可以表示为一条从顶点u{\displaystyle u}到v{\displaystyle v}的（不闭合的）欧拉路径的充要条件是：u{\displaystyle u}的出度（从这个顶点发出的有向边的数量）比入度（指向这个顶点的有向边的数量）多1，v{\displaystyle v}的出度比入度少1，而其它顶点的出度和入度都相等。

一个连通的有向图是欧拉环（存在欧拉回路）的充要条件是以下两个之一：

例子

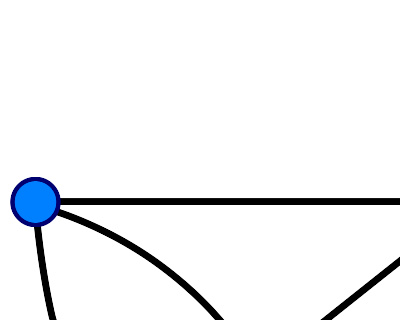
图一：无法一笔画

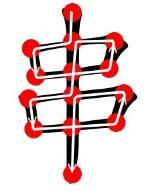
图二：尽管按照中文书写习惯“串”字不止一笔，但它可以一笔写成。

七桥问题

右图一是七桥问题抽象化后得到的模型，由四个顶点和七条边组成。注意到四个顶点全是奇顶点，由定理一可知无法一笔画成。

一个可以一笔画的例子

图二是中文“串”字抽象化后得到的模型。由于只有最上方和最下方的顶点是奇顶点，由定理一知它可以一笔画成。

一笔画问题与哈密顿问题

一笔画问题讨论的是能否不重复地遍历一个图的所有边，至于其中有否顶点的遍历或重复经过则没有要求。哈密顿问题讨论的则是顶点的遍历：能否不重复地遍历一个图的所有顶点？哈密顿问题由哈密顿在1856年首次提出，至今尚未完全解决。

参见

柯尼斯堡七桥问题

哈密尔顿问题

树 (图论)

中国邮递员问题

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。