物理学

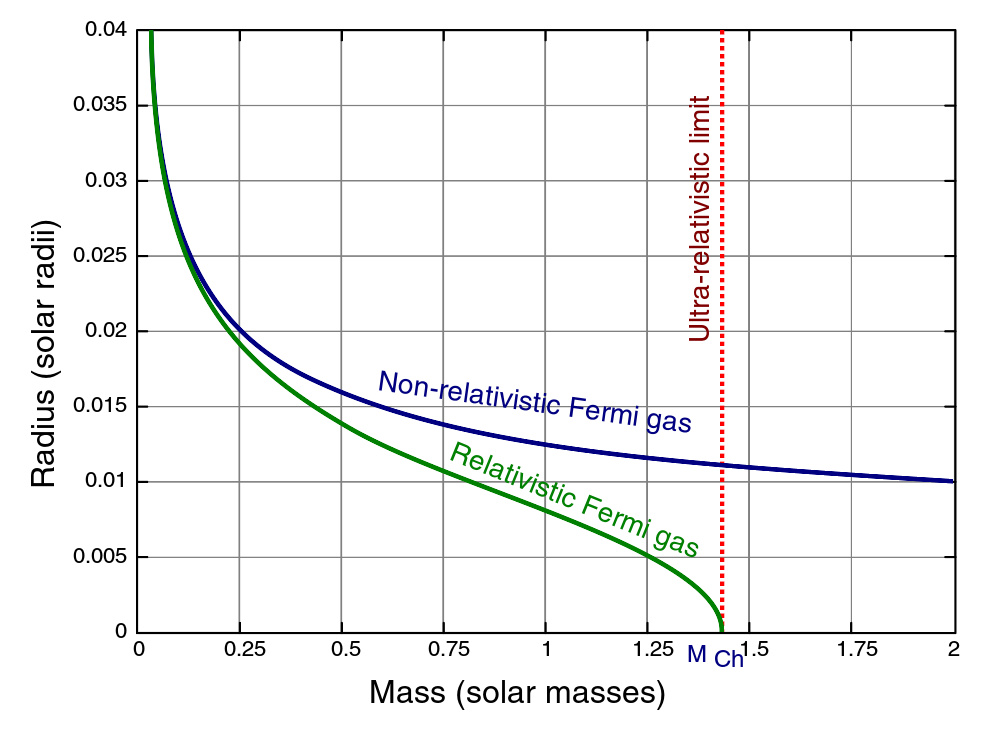
  白矮星模型的半径相对于质量图。

电子简并压力是依据量子力学的泡利不相容原理所产生的效应。因为电子是费米子，在一个原子内不能有两个电子有着相同的量子状态，所以不可能让所有的电子都在最低的能量。换言之，电子必然会占有不同的能阶。当原子被压缩时，由于电子的数量和必须占有不同的能阶，所以必然会占有一定量的体积。因此电子的能量将因为压缩而增加，电子也必须施加压力来抗拒电子云的进一步压缩。这就是电子简并压力的起源。

在非相对论的情况下，电子简并压力可以由状态方程求得，形式为P=K 1 ρ 。解白矮星多方模型的流体静力学等效方程式可以导出系数为3/2的半径反比于质量的立方，和体积反比于质量的关系。 当白矮星模型的质量增加时，电子简并压力使得特有的电子能量相对于它们的静止质量不再是微不足道的。电子的速度接近光速，因此必须考虑到狭义相对论。在强大的相对论效应下，我们发现状态方程的形式为P=K 2 ρ 。这将使多方模型的系数成为3，这会使总质量M limit 只与K 2 相关联。.

延伸读物

On Stars, Their Evolution and Their Stability, Nobel Prize lecture, Subrahmanyan Chandrasekhar, December 8, 1983.

White dwarf stars and the Chandrasekhar limit, Masters" thesis, Dave Gentile,帝博大学, 1995.

Estimating Stellar Parameters from Energy Equipartition, sciencebits.com. Discusses how to find mass-radius relations and mass limits for white dwarfs using simple energy arguments.

相关条目

简并物质

托尔曼－奥本海默－沃尔科夫方程

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。