简介

亥姆霍兹线圈是由一对完全相同的圆形导体线圈组成。采用直角坐标系，这两个半径为R{\displaystyle R}的圆形线圈的中心轴都与z-轴同轴。两个圆形线圈的z-坐标分别为h/2{\displaystyle h/2}与− − -->h/2{\displaystyle -h/2}。每一个导体线圈载有同向电流I{\displaystyle I}。

设定h=R{\displaystyle h=R}可以使得在两个线圈中心位置O（即原点）的磁场，其不均匀程度极小化。这动作促使∂ ∂ -->2B/∂ ∂ -->z2=0{\displaystyle \partial ^{2}B/\partial z^{2}=0}，也意味着领先的非零微分项目是∂ ∂ -->4B/∂ ∂ -->z4{\displaystyle \partial ^{4}B/\partial z^{4}}，稍后会对这论点做更详细解释。但是，这样做仍旧会在线圈平面跟z-轴相交处与O点之间遗留大约7%磁场数值的差别。

在某些应用中，亥姆霍兹线圈可以用来抵消地磁场，制造出接近零磁场的区域。

数学描述

在亥姆霍兹线圈的二等分面的磁场线。注意到在两个线圈之间的磁场近似均匀（在这电脑绘图里，线圈的中心轴是纵向的）。

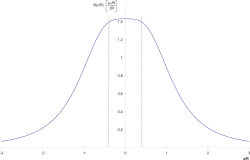
沿着线圈中心轴（z-轴）的磁场。与两个线圈同距离的中心位置的z-坐标为0。

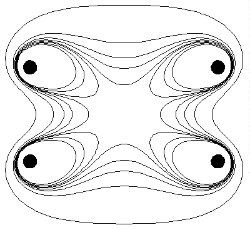
等值线图显示出在亥姆霍兹线圈的磁场的数值大小。在中央的章鱼区域内，磁场数值与中心位置的磁场数值B0{\displaystyle B_{0}}相差不超过1%。五条等值线的磁场数值分别为0.5B0{\displaystyle 0.5B_{0}}、0.8B0{\displaystyle 0.8B_{0}}、0.9B0{\displaystyle 0.9B_{0}}、0.95B0{\displaystyle 0.95B_{0}}、0.99B0{\displaystyle 0.99B_{0}}。

关于在空间任意位置的精确磁场计算，需要应用到贝索函数或椭圆函数与其相关技巧。沿着线圈的中心轴（z-轴），涉及到的计算比较简单，可以应用泰勒展开，将磁场展开为z{\displaystyle z}的幂级数。采用直角坐标系，以亥姆霍兹线圈的中心位置为z-轴的原点O。由于对于xy-平面的对称性，奇数幂项目必等于零。经过调整两个线圈之间的距离h{\displaystyle h}，可以使得O点成为拐点，则可以保证z2{\displaystyle z^{2}}级项目为零，因此领先不均匀项目是z4{\displaystyle z^{4}}级项目。

在中心位置O点，磁场为

其中，μ μ -->0{\displaystyle \mu _{0}}是磁常数。

推导

采用直角坐标系，设定单匝线圈的中心轴为z-轴，线圈平面与z-轴相交处为原点，则在z-轴的磁场以方程式表示为（这方程式可以从必欧-沙伐定律推导出来）

其中，B{\displaystyle B}是磁场数值大小，μ μ -->0{\displaystyle \mu _{0}}是磁常数，I{\displaystyle I}是电流，R{\displaystyle R}是线圈半径，z{\displaystyle z}是检验位置的z-坐标。

对于n{\displaystyle n}匝线圈，磁场为

现在改变系统为亥姆霍兹线圈，其中心位置为原点。原点与线圈平面之间的垂直距离为R/2{\displaystyle R/2}，注意到每一个亥姆霍兹线圈有一对线圈，所以，总磁场为

进阶推导

更详细地计算，沿着z-轴的磁场为两个线圈的贡献的叠加：

在原点附近的磁场，经过一番运算，可以泰勒展开成z{\displaystyle z}的幂级数：

其中，d=R2+h2/4{\displaystyle d={\sqrt {R^{2}+h^{2}/4}}}。

现在设定h=R{\displaystyle h=R}，则z2{\displaystyle z^{2}}项目为零，在原点附近的磁场更加均匀：

磁场不均匀率与z{\displaystyle z}的关系式为

在z=± ± -->R/2{\displaystyle z=\pm R/2}，线圈平面与z-轴相交处，磁场数值的差别为

参阅

麦克斯韦线圈（Maxwell coils）

亥姆霍兹共鸣（英语：Helmholtz resonance）

螺线管

磁振造影

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。