预备知识

下边的讨论要求读者熟悉概率论中的基本定义，如概率分布、概率密度函数、随机变量、数学期望等。同时，还要求读者熟悉连续实函数的基本技巧，比如使用微分来求一个函数的极值（即极大值或极小值）。

最大似然估计的原理

给定一个概率分布 D {\displaystyle D} ，已知其概率密度函数（连续分布）或概率质量函数（离散分布）为 f D {\displaystyle f_{D}} ，以及一个分布参数 θ θ --> {\displaystyle \theta } ，我们可以从这个分布中抽出一个具有 n {\displaystyle n} 个值的采样 X 1 , X 2 , … … --> , X n {\displaystyle X_{1},X_{2},\ldots ,X_{n}} ，利用 f D {\displaystyle f_{D}} 计算出其概率：

但是，我们可能不知道 θ θ --> {\displaystyle \theta } 的值，尽管我们知道这些采样数据来自于分布 D {\displaystyle D} 。那么我们如何才能估计出 θ θ --> {\displaystyle \theta } 呢？一个自然的想法是从这个分布中抽出一个具有 n {\displaystyle n} 个值的采样 X 1 , X 2 , . . . , X n {\displaystyle X_{1},X_{2},...,X_{n}} ，然后用这些采样数据来估计 θ θ --> {\displaystyle \theta } .

一旦我们获得 X 1 , X 2 , … … --> , X n {\displaystyle X_{1},X_{2},\ldots ,X_{n}} ，我们就能求得一个关于 θ θ --> {\displaystyle \theta } 的估计。最大似然估计会寻找关于 θ θ --> {\displaystyle \theta } 的最可能的值（即，在所有可能的 θ θ --> {\displaystyle \theta } 取值中，寻找一个值大化个采样的“可能性”最大化）。这种方法正好同一些其他的估计方法不同，如 θ θ --> {\displaystyle \theta } 的非偏估计，非偏估计未必会输出一个最可能的值，而是会输出一个既不高估也不低估的 θ θ --> {\displaystyle \theta } 值。

要在数学上实现最大似然估计法，我们首先要定义似然函数:

并且在 θ θ --> {\displaystyle \theta } 的所有取值上通过令一阶导数等于零，使这个函数取到最大值。这个使可能性最大的 θ θ --> ^ ^ --> {\displaystyle {\widehat {\theta }}} 值即称为 θ θ --> {\displaystyle \theta } 的 最大似然估计 。

注意

这里的似然函数是指 x 1 , x 2 , … … --> , x n {\displaystyle x_{1},x_{2},\ldots ,x_{n}} 不变时，关于 θ θ --> {\displaystyle \theta } 的一个函数。

最大似然估计函数不一定是惟一的，甚至不一定存在。

例子

离散分布，离散有限参数空间

考虑一个抛硬币的例子。假设这个硬币正面跟反面轻重不同。我们把这个硬币抛80次（即，我们获取一个采样 x 1 = H , x 2 = T , … … --> , x 80 = T {\displaystyle x_{1}={\mbox{H}},x_{2}={\mbox{T}},\ldots ,x_{80}={\mbox{T}}} 并把正面的次数记下来，正面记为H，反面记为T）。并把抛出一个正面的概率记为 p {\displaystyle p} ，抛出一个反面的概率记为 1 − − --> p {\displaystyle 1-p} （因此，这里的 p {\displaystyle p} 即相当于上边的 θ θ --> {\displaystyle \theta } ）。假设我们抛出了49个正面，31个反面，即49次H，31次T。假设这个硬币是我们从一个装了三个硬币的盒子里头取出的。这三个硬币抛出正面的概率分别为 p = 1 / 3 {\displaystyle p=1/3} , p = 1 / 2 {\displaystyle p=1/2} , p = 2 / 3 {\displaystyle p=2/3} .这些硬币没有标记，所以我们无法知道哪个是哪个。使用 最大似然估计 ，通过这些试验数据（即采样数据），我们可以计算出哪个硬币的可能性最大。这个似然函数取以下三个值中的一个：

我们可以看到当 p ^ ^ --> = 2 / 3 {\displaystyle {\widehat {p}}=2/3} 时，似然函数取得最大值。这就是 p {\displaystyle p} 的最大似然估计。

离散分布，连续参数空间

现在假设例子1中的盒子中有无数个硬币，对于 0 ≤ ≤ --> p ≤ ≤ --> 1 {\displaystyle 0\leq p\leq 1} 中的任何一个 p {\displaystyle p} ， 都有一个抛出正面概率为 p {\displaystyle p} 的硬币对应，我们来求其似然函数的最大值：

其中 0 ≤ ≤ --> p ≤ ≤ --> 1 {\displaystyle 0\leq p\leq 1} . 我们可以使用微分法来求最值。方程两边同时对 p {\displaystyle p} 取微分，并使其为零。

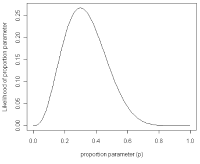
在不同比例参数值下一个二项式过程的可能性曲线 t = 3, n = 10；其最大似然估计值发生在其众数并在曲线的最大值处。

其解为 p = 0 {\displaystyle p=0} , p = 1 {\displaystyle p=1} ，以及 p = 49 / 80 {\displaystyle p=49/80} .使可能性最大的解显然是 p = 49 / 80 {\displaystyle p=49/80} （因为 p = 0 {\displaystyle p=0} 和 p = 1 {\displaystyle p=1} 这两个解会使可能性为零）。因此我们说 最大似然估计值 为 p ^ ^ --> = 49 / 80 {\displaystyle {\widehat {p}}=49/80} .

这个结果很容易一般化。只需要用一个字母 t {\displaystyle t} 代替49用以表达伯努利试验中的被观察数据（即样本）的“成功”次数，用另一个字母 n {\displaystyle n} 代表伯努利试验的次数即可。使用完全同样的方法即可以得到 最大似然估计值 :

对于任何成功次数为 t {\displaystyle t} ，试验总数为 n {\displaystyle n} 的伯努利试验。

连续分布，连续参数空间

最常见的连续概率分布是正态分布，其概率密度函数如下：

现在有 n {\displaystyle n} 个正态随机变量的采样点，要求的是一个这样的正态分布，这些采样点分布到这个正态分布可能性最大（也就是概率密度积最大，每个点更靠近中心点），其 n {\displaystyle n} 个正态随机变量的采样的对应密度函数（假设其独立并服从同一分布）为：

或：

这个分布有两个参数： μ μ --> , σ σ --> 2 {\displaystyle \mu ,\sigma ^{2}} .有人可能会担心两个参数与上边的讨论的例子不同，上边的例子都只是在一个参数上对可能性进行最大化。实际上，在两个参数上的求最大值的方法也差不多：只需要分别把可能性 lik ( μ μ --> , σ σ --> ) = f ( x 1 , , … … --> , x n ∣ ∣ --> μ μ --> , σ σ --> 2 ) {\displaystyle {\mbox{lik}}(\mu ,\sigma )=f(x_{1},,\ldots ,x_{n}\mid \mu ,\sigma ^{2})} 在两个参数上最大化即可。当然这比一个参数麻烦一些，但是一点也不复杂。使用上边例子同样的符号，我们有 θ θ --> = ( μ μ --> , σ σ --> 2 ) {\displaystyle \theta =(\mu ,\sigma ^{2})} .

最大化一个似然函数同最大化它的自然对数是等价的。因为自然对数log是一个连续且在似然函数的值域内严格递增的上凸函数。[注意：可能性函数（似然函数）的自然对数跟信息熵以及Fisher信息联系紧密。]求对数通常能够一定程度上简化运算，比如在这个例子中可以看到：

这个方程的解是 μ μ --> ^ ^ --> = x ¯ ¯ --> = ∑ ∑ --> i = 1 n x i / n {\displaystyle {\widehat {\mu }}={\bar {x}}=\sum _{i=1}^{n}x_{i}/n} .这的确是这个函数的最大值，因为它是 μ μ --> {\displaystyle \mu } 里头惟一的一阶导数等于零的点并且二阶导数严格小于零。

同理，我们对 σ σ --> {\displaystyle \sigma } 求导，并使其为零。

这个方程的解是 σ σ --> ^ ^ --> 2 = ∑ ∑ --> i = 1 n ( x i − − --> μ μ --> ^ ^ --> ) 2 / n {\displaystyle {\widehat {\sigma }}^{2}=\sum _{i=1}^{n}(x_{i}-{\widehat {\mu }})^{2}/n} .

因此，其关于 θ θ --> = ( μ μ --> , σ σ --> 2 ) {\displaystyle \theta =(\mu ,\sigma ^{2})} 的 最大似然估计 为：

性质

泛函不变性（Functional invariance）

如果 θ θ --> ^ ^ --> {\displaystyle {\widehat {\theta }}} 是 θ θ --> {\displaystyle \theta } 的一个最大似然估计，那么 α α --> = g ( θ θ --> ) {\displaystyle \alpha =g(\theta )} 的最大似然估计是 α α --> ^ ^ --> = g ( θ θ --> ^ ^ --> ) {\displaystyle {\widehat {\alpha }}=g({\widehat {\theta }})} .函数 g 无需是一个一一映射。请参见George Casella与Roger L. Berger所著的 Statistical Infer中国ce 定理Theorem 7.2.10的证明。（出版的大部分教材上也可以找到这个证明。）

渐近线行为

最大似然估计函数在采样样本总数趋于无穷的时候达到最小方差（其证明可见于Cramer-Rao lower bound）。当最大似然估计非偏时，等价的，在极限的情况下我们可以称其有最小的均方差。 对于独立的观察来说，最大似然估计函数经常趋于正态分布。

偏差

最大似然估计的偏差是非常重要的。考虑这样一个例子，标有 1 到 n 的 n 张票放在一个盒子中。从盒子中随机抽取票。如果 n 是未知的话，那么 n 的最大似然估计值就是抽出的票上标有的 n ，尽管其期望值的只有 ( n + 1 ) / 2 {\displaystyle (n+1)/2} .为了估计出最高的 n 值，我们能确定的只能是 n 值不小于抽出来的票上的值。

历史

最大似然估计最早是由罗纳德·费雪在1912年至1922年间推荐、分析并大范围推广的。 （虽然以前高斯、拉普拉斯、T. N. Thiele和 F. Y. 埃奇沃思 （ 英语 ： Francis Ysidro Edgeworth ） 也使用过）。 许多作者都提供了最大似然估计发展的回顾。

大部分的最大似然估计理论都在贝叶斯统计中第一次得到发展，并被后来的作者简化。

参见

均方差是衡量一个估计函数的好坏的一个量。

关于Rao-Blackwell定理（Rao-Blackwell theorem）的文章里头讨论到如何利用Rao-Blackwellisation过程寻找最佳非偏估计（即使均方差最小）的方法。而最大似然估计通常是一个好的起点。

读者可能会对最大似然估计（如果存在）总是一个关于参数的充分统计（sufficient statistic）的函数感兴趣。

最大似然估计跟一般化矩方法（generalized method of moments）有关。

外部资源

关于最大似然估计的历史的一篇论文，作者John Aldrich

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。