性质

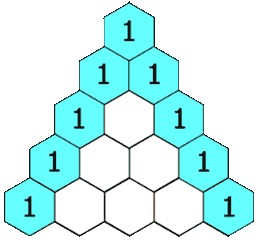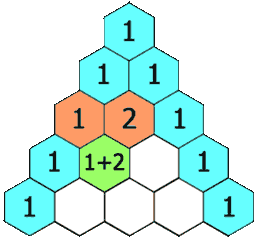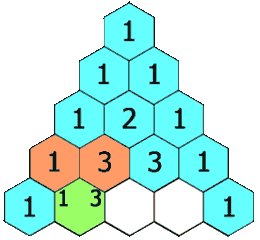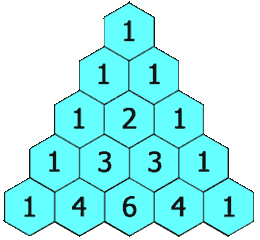
  每个数是它左上方和右上方的数的和

杨辉三角以正整数构成，数字左右对称，每行由1开始逐渐变大，然后变小，回到1。

第 n {\displaystyle n} 行的数字个数为 n {\displaystyle n} 个。

第 n {\displaystyle n} 行的第 k {\displaystyle k} 个数字为组合数 C n − − --> 1 k − − --> 1 {\displaystyle C_{n-1}^{k-1}} 。

第 n {\displaystyle n} 行数字和为 2 n − − --> 1 {\displaystyle 2^{n-1}} 。

除每行最左侧与最右侧的数字以外，每个数字等于它的左上方与右上方两个数字之和（也就是说，第 n {\displaystyle n} 行第 k {\displaystyle k} 个数字等于第 n − − --> 1 {\displaystyle n-1} 行的第 k − − --> 1 {\displaystyle k-1} 个数字与第 k {\displaystyle k} 个数字的和）。这是因为有组合恒等式： C n i = C n − − --> 1 i − − --> 1 + C n − − --> 1 i {\displaystyle C_{n}^{i}=C_{n-1}^{i-1}+C_{n-1}^{i}} 。可用此性质写出整个杨辉三角形。

历史

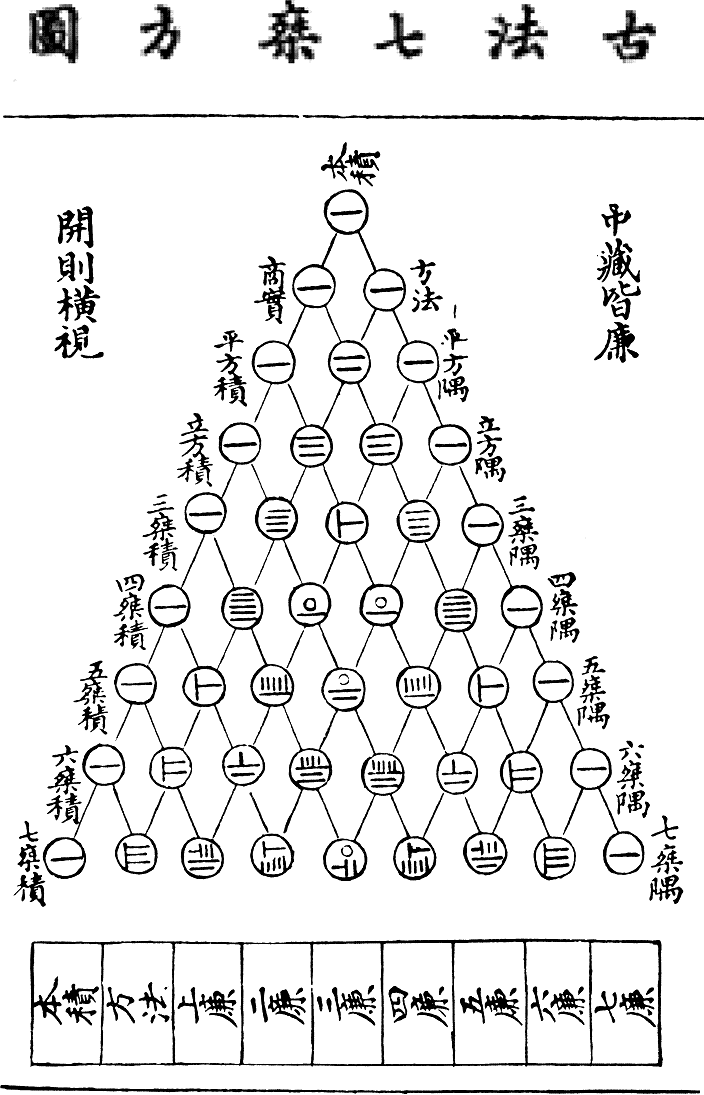
  朱世杰《四元玉鉴》中的“古法七乘方图”

波斯数学家Karaji和天文学家兼诗人欧玛尔·海亚姆（عمر خیام,Omar Khayyám）在10世纪都发现了这个三角形，而且还知道可以借助这个三角形找 n {\displaystyle n} 次根，和它跟二项式的关系。但他们的著作已不存。

11世纪北宋数学家贾宪发明了贾宪三角，并发明了增乘方造表法，可以求任意高次方的展开式系数。贾宪还对贾宪三角表（古代称数字表为“立成”）的构造进行描述。 。贾宪的三角表图和文字描写，仍保存在大英博物馆所藏《永乐大典》卷一万六千三百四十四。

13世纪中国南宋数学家杨辉在《详解九章算术》里解释这种形式的数表，并说明此表引自11世纪前半贾宪的《释锁算术》 。

1303年元代数学家朱世杰在《四元玉鉴》卷首绘制《古法七乘方图》 。

意大利人称之为“塔塔利亚三角形”（Triangolo di Tartaglia）以纪念在16世纪发现一元三次方程解的塔塔利亚。

布莱士·帕斯卡的著作 Traité du triangle arithmétique （1655年）介绍了这个三角形。帕斯卡搜集了几个关于它的结果，并以此解决一些概率论上的问题，影响面广泛，Pierre Raymond de Montmort（1708年）和亚伯拉罕·棣莫弗（1730年）都用帕斯卡来称呼这个三角形。

历史上曾经独立绘制过这种图表的数学家：

Karaji 和 Omar Khayyám 波斯 10世纪（图文无存）

贾宪 中国北宋 11世纪 《释锁算术》 （图文现存大英博物馆所藏《永乐大典》）

杨辉 中国南宋 1261《详解九章算法》记载之功（图文现存大英博物馆所藏《永乐大典》）

朱世杰 中国元代 1299《四元玉鉴》级数求和公式

阿尔·卡西 阿拉伯 1427《算术的钥匙》 （现存图文）

阿皮亚纳斯 德国 1527

施蒂费尔 德国 1544《综合算术》二项式展开式系数

薛贝尔 法国 1545

B·帕斯卡 法国 1654《论算术三角形》

中国数学家的研究

中国贾宪是 贾宪三角 的发明人，贾宪/杨辉称之为“释锁求廉本源”，朱世杰称之为“古法七乘方图”(1303年），明代数学家吴敬《九章详注比类算法大全》称之为“开方作法本源”（1450年）；明王文素《算学宝鉴》称之为“开方本源图”（1524年）；明代程大位《算法统宗》称之为“开方求廉率作法本源图”（1592年）。 清代梅文鼎《少广拾遗》称之为“七乘府算法”（1692年）；清代孔广森《少广正负术》称之为“诸乘方乘率表”；焦循《加减乘除释》称之为“古开方本原图”；刘衡《筹表开诸乘方捷法》称之为“开方求廉率图”；项名达《象数一原》称之为“递加图”。伟烈亚力《数学启蒙》称之为“倍廉法表”；李善兰《垛积比类》称之为“三角垛表”。近代中算史家李俨称之为“巴斯噶三角形”，但根据《永乐大典》指出“巴斯噶三角形”最早由贾宪使用。 。著名数学家华罗庚，在1956年写的一本通俗读物《从杨辉三角谈起》 ，将贾宪的《开方作法本源》称为“杨辉三角”，首次将“巴斯噶三角形”回归宋代数学家名下；此后的中学数学教科书和许多数学科普读物都跟随之 。另一方面，专业的中国数学史著作，都用“贾宪三角”这个称呼。 。

一个数在杨辉三角出现的次数

由1开始，正整数在杨辉三角形出现的次数为：∞,1, 2, 2, 2, 3, 2, 2, 2, 4, 2, 2, 2, 2, 4, ... （OEIS:A003016）。最小而又大于1的数在贾宪三角形至少出现n次的数为2, 3, 6, 10, 120, 120, 3003, 3003, ... （OEIS:A062527）

除了1之外，所有正整数都出现有限次。

只有2出现刚好一次。

6,20,70等出现三次。

出现两次和四次的数很多。

还未能找到出现刚好五次或七次的数。

120,210,1540等出现刚好六次。（OEIS:A098565）

3003是第一个出现八次的数。

参见

贾宪、杨辉

莱布尼茨三角形

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。