定义

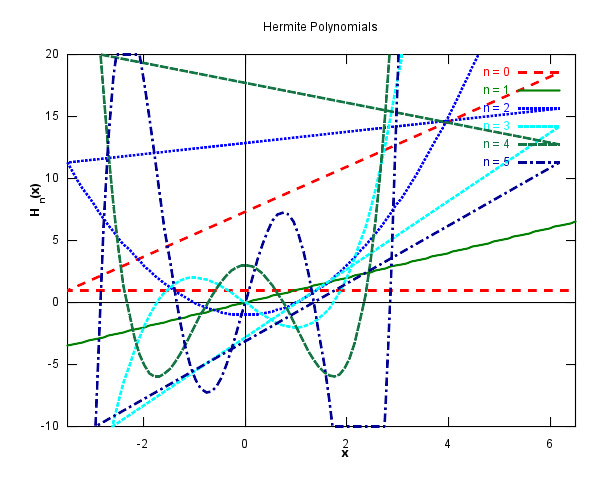
前六个（概率论中的）埃尔米特多项式的图像。

埃尔米特多项式有两种常见定义。

第一种是概率论中较为常用的形式（又记作：Hnprob(x){\displaystyle H_{n}^{\mathrm {prob} }(x)}）：

另一种是物理学中较为常用的形式（又记作：Hnphys(x){\displaystyle H_{n}^{\mathrm {phys} }(x)}）：

这两种定义并不是完全等价的。它们之间的关系是：

概率论中常用第一种定义，因为e− − -->x2/22π π -->{\displaystyle {\frac {e^{-x^{2}/2}}{\sqrt {2\pi }}}}是标准正态分布函数（数学标准差于0，标准差等于1）的概率密度函数。

前六个（物理学中的）埃尔米特多项式的图像。

性质

多项式Hn 是一个n次的多项式。概率论的埃尔米特多项式是首一多项式（最高次项系数等于1），而物理学的埃尔米特多项式的最高次项系数等于2。

正交性

多项式Hn 的次数与序号n 相同，所以不同的埃尔米特多项式的次数不一样。对于给定的权函数w，埃尔米特多项式的序列将会是正交序列。

也就是说，当m ≠ n 时：

除此之外，还有：

其中δ δ -->mn{\displaystyle \delta _{mn}}是克罗内克函数。

从上式可以看到，概率论中的埃尔米特多项式与标准正态分布正交。

完备性

在所有满足

的函数所构成的完备空间中，埃尔米特多项式序列构成一组基。其中的内积定义如下：

埃尔米特微分方程

概率论中的埃尔米特多项式是以下微分方程的解:

方程的的边界条件为：u{\displaystyle u}应在无穷远处有界。

其中λ λ -->{\displaystyle \lambda }是这个方程的本征值，是一个常数。要满足上述边界条件，应取λ λ -->{\displaystyle \lambda }∈N{\displaystyle \mathbb {N} }。对于一个特定的本征值λ λ -->{\displaystyle \lambda }，对应着一个特定的本征函数解，即Hλ λ -->prob(x){\displaystyle H_{\lambda }^{prob}(x)}。

而物理学中的埃尔米特多项式则是以下微分方程的解:

其本征值同样为λ λ -->{\displaystyle \lambda }∈N{\displaystyle \mathbb {N} }，对应的本征函数解为Hλ λ -->phys(x){\displaystyle H_{\lambda }^{phys}(x)}。

以上两个微分方程都称为埃尔米特方程。

参考文献

Arfken, Mathematical Methods for Physicists

B Spain, M G Smith, Functions of mathematical physics, Van Nostrand Reinhold Company, London, 1970. Chapter 11 deals with Hermite polynomials.

Bayin, S.S. (2006) Mathematical Methods in Science and Engineering, Wiley, Chapter 4.

Courant, Richard; Hilbert, David, Methods of Mathematical Physics, Volume I, Wiley-Interscience, 1953 .

Erdélyi, Arthur; Magnus, Wilhelm; Oberhettinger, Fritz; Tricomi, Francesco G., Higher transcendental functions. Vol. II, McGraw-Hill, 1955 

Fedoryuk, M.V.,H/h046980, (编) Hazewinkel, Michiel,数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4 .

Szegő, Gábor, Orthogonal Polynomials, American Mathematical Society, 1939, 1955 

Wiener, Norbert, The Fourier Integral and Certain of its Applications, New York: Dover Publications, 1958, ISBN 0-486-60272-9 

Whittaker, E. T.; Watson, G. N. A Course of Modern Analysis 4th Edition. London: Cambridge University Press. 1962. 引文格式1维护：冗余文本 (link)

Temme, Nico, Special Functions: An Introduction to the Classical Functions of Mathematical Physics, Wiley, New York, 1996

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。