作品尽管尼波斯在生前便受到不少赞誉，但其作品几乎全部失佚了。因此对于尼波斯作品的了解几乎全都来源于其他罗马作家的引用和提及。其中一个重要的例子是格利乌斯的《阿提卡之夜》。尼波斯现知的作品包括：《事纪》（Chronica）。有观点认为卡图卢斯在其开卷诗中提到的就是此作；奥索尼乌斯也在其信件中提及此书；格利乌斯也曾在《阿提卡之夜》中提及。《名人传》（DeVirisIllustribus）。格利乌斯引用了此书的一个关于老卡托的事迹。《西塞罗传》（DeVitaCiceronis）。格利乌斯曾纠正其一个错误。致西塞罗的书信（EpistulaeadCiceronem）。其中一部分因为拉克坦尼乌斯的引用而保留下来。小普林尼曾提及其诗歌作品。尼波斯本人也在《迪昂传》（Dion）中提到了自己的作品《论历史家》（DeHistoricis）尼波斯唯一的现存作品是《伟人传》（ExcellentiumImperat...

出演作品电影WelcometotheDollhouse(1995)IShotAndyWarhol(1996)LawnDogs（1997）TheMinusMan(1999)CruelIntentions(1999)TheCrow:Salvation(2000)Tempted(2001)生化危机(电影)(2002)TheJob(2003)生化危机2：启示录(2004)VeniceUnderground(2005)电视剧芝加哥希望ChicagoHope(1997)犯罪现场调查：迈阿密CSI:Miami(2002)色欲L世代TheLWord(2004-2006)橘郡风云TheO.C.(2005)丑女贝蒂UglyBetty(2006-)参考资料

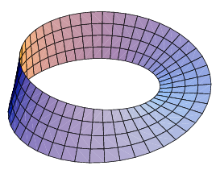
几何学与拓扑学结构用Matlab描绘的莫比乌斯带一个利用参数方程式创造出立体莫比乌斯带的方法：这个方程组可以创造一个边长为1半径为1的莫比乌斯带，所处位置为x-y面，中心为（0，0，0）。参数u在v从一个边移动到另一边的时候环绕整个带子。如果用圆柱坐标系（r,θ,z）表示的话，一个无边界的莫比乌斯带可以表示为：从拓扑学上来讲，莫比乌斯带可以定义为矩阵[0,1]×[0,1]，边由在0≤x≤1的时候（x,0）~（1-x,1）决定，如右图所示。莫比乌斯带是一个二维的紧致流形（即一个有边界的面），可以嵌入到三维或更高维的流形中。它是一个不可定向的的标准范例，可以看作RP#RP。同时也是数学上描绘纤维丛的例子之一。特别地，它是一个有一纤维单位区间，I=[0,1]的圆S上的非平凡丛。仅从莫比乌斯带的边缘看去给出S上一个非平凡的两个点（或Z2）的从。有关的物体和莫比乌斯带非常近似的一个几何学物体叫做克莱...

简介莫比乌斯变换是定义在扩充复平面上的（扩充复平面是指在普通的复平面加入无穷远点构成的集合）扩充复平面可以看做是一个球面，它的另一个名称就是黎曼球面。每个莫比乌斯变换都是从黎曼球面到它自身的一一对应的共形变换。事实上，所有这样的变换都是莫比乌斯变换。所有莫比乌斯变换的集合在函数复合作用下构成一个群，称为“莫比乌斯群”，记作M(C^^-->){\displaystyle{\mathcal{M}}({\widehat{\mathbb{C}}})}。这个群是黎曼球面（作为一个黎曼曲面）的自同构群，因此有时也被记作：莫比乌斯群同构于三维双曲空间中的保向等距同构群，因此在三维双曲空间中的子流形的研究中占有重要地位。定义莫比乌斯变换的常见形式为：其中a、b、c、d是任何满足ad−bc≠0的复数（当ad=bc的时候这个表达式退化成一个常数，通常约定常数函数不是莫比乌斯变换）。当c≠0时，定义这样便将莫比...

定义假设对于数论函数f(n)和F(n)，有以下关系式：F(n)=∑∑-->d|nf(d){\displaystyleF(n)=\sum_{d|n}f(d)}则将其默比乌斯反转公式定义为：f(n)=∑∑-->d|nμμ-->(d)F(nd){\displaystylef(n)=\sum_{d|n}\mu(d)F\left({\frac{n}{d}}\right)}一般形式设F(x){\displaystyleF(x)}及G(x){\displaystyleG(x)}为定义在[1,∞∞-->){\displaystyle[1,\infty)}上的复值函数并且G(x)=∑∑-->1⩽⩽-->n⩽⩽-->xF(xn){\displaystyleG(x)=\sum_{1\leqslantn\leqslantx}F\left({\frac{x}{n}}\rig...