内容

《测圆海镜》由卷一的 圆城图式 、说明各个长度名称的 总率名号 、给出各个长度数值的 今问正数 、囊括了各个量之间关系的公式总集 识别杂记 ；卷二至卷十二，共一百七十个问题及其解答所组成。书中一共有148问，182种方法是以天元术列出方程以求解，其中列出一次方程31个，二次方程106个，三次方程24个，四次方程20个，六次方程1个

卷一

圆城图式

圆城图式（右图）是全书的总括图解，由一个直角三角形（古时称为勾股形）、它的内切圆以及一些特定的点和直线组成。其中的顶点、圆心和交点都用某个汉字来指代。最大的三角形的三个顶点分别是 天 、 地 、 干 ， 天地干 三角形的内切圆圆心称为 心 。过 心 的垂直线从上至下分别和三角形、内切圆交于 日 、 南 、 北 三点。过 心 的水平线从左至右分别和三角形、内切圆交于 川 、 东 、 西 三点。过 东 的垂直线和过 南 的水平线都是内切圆的切线，它们分别交 天地干 三角形于 艮 、 坤 、 山 、 月 四点，而相交于 巽 点。 乾坤巽艮 构成一个正方形。过 月 的垂直线交 东西 水平线于 青 点，交 地干 边于 泉 点。过 山 的水平线交 南北 垂直线于 朱 点，交 天干 边于 金 点。而这两条线相交于 泛 点。最后过 日 的水平线交 天干 边于 旦 点，过 川 的垂直线交 地干 边于 夕 点。总共22个点。

总率名号

全书所研究的三角形一共有15个，全部是以 天地 线之间的线段为弦（斜边）的直角三角形。总率名号给出了这些三角形和线段的名称。它们分别是：

其中弦是三角形斜边，股是三角形的长直角边（这里是竖直的），勾是三角形短直角边（这里是水平的）。（ a 1 {\displaystyle a_{1}} 代表通勾， b 1 {\displaystyle b_{1}} 代表通股， c 1 {\displaystyle c_{1}} 代表通弦，余类推）。

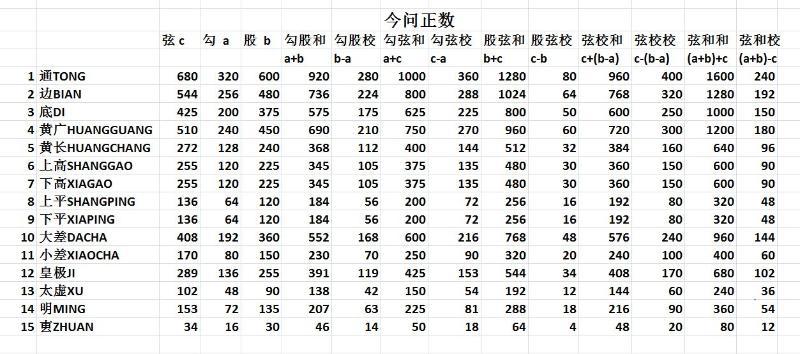
今问正数

今问正数一节给出了圆城图式中每个线段的长度。其中以内切圆的半径为120步，作为标准。

:弦

:勾

:股

:勾股和：a+b

:勾股校：b-a

:勾弦和：a+c

:勾弦校：c-a

:股弦和：b+c

:股弦校：c-b

:弦校和：c+(b-a)

:弦校校：c-(b-a)

:弦和和：（a+b)+c

:弦和校：（a+b)-c

例子:“通弦六百八十，勾三百二十，股六百；勾股和九百二十，较（两者的差）二百八十；勾弦和一千，较三百六十；股弦和一千二百八十，较八十；弦较和九百六十，较四百；弦和和一千六百，较二百四十。”

15个勾股形中上高 = 下高；上平=下平，因此，15个勾股形中，只有13个勾股形是相异的。

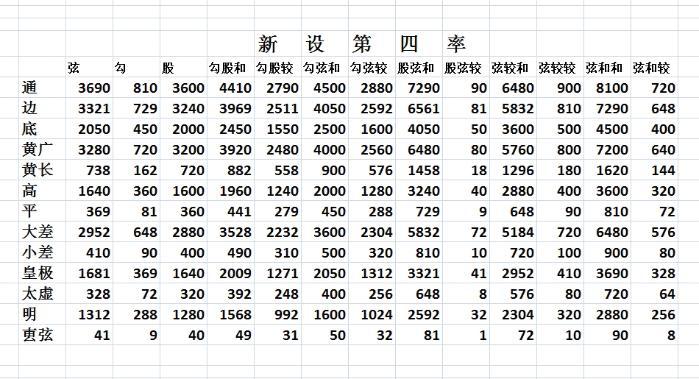
《今问正数》共15个勾股形×13项=195项 。 ，列表如下。

识别杂记

识别杂记都是关于不同线段之间的几何关系式。一共给出了692个公式。是全书的纲领。

识别杂记包含八项：

诸杂名目：是全书的总纲，列出各项定义，例如虚勾虚股相得名为虚率，高股平勾差名为角差，又名远差等等。诸杂名目中还列出三十余项定理，如凡大差小差相乘为半段径幂，大差勾小差股相乘同上、黄广股黄长勾相乘为经幂等等。

名目

杂用公式

( c 1 − − --> a 1 ) ∗ ∗ --> ( c 1 ∗ ∗ --> b 1 ) {\displaystyle (c_{1}-a_{1})*(c_{1}*b_{1})} = 1 2 {\displaystyle 1 \over 2} * ( d 1 ) 2 {\displaystyle (d_{1})^{2}}

a 10 ∗ ∗ --> b 11 {\displaystyle a_{10}*b_{11}} = 1 2 {\displaystyle 1 \over 2} ( d 1 ) 2 {\displaystyle (d_{1})^{2}}

a 13 ∗ ∗ --> b 1 {\displaystyle a_{13}*b_{1}} = 1 2 {\displaystyle 1 \over 2} ( d 1 ) 2 {\displaystyle (d_{1})^{2}}

a 1 ∗ ∗ --> b 13 {\displaystyle a_{1}*b_{13}} = 1 2 {\displaystyle 1 \over 2} ( d 1 ) 2 {\displaystyle (d_{1})^{2}}

b 2 ∗ ∗ --> b 15 {\displaystyle b_{2}*b_{15}} = ( r 1 ) 2 {\displaystyle (r_{1})^{2}}

a 14 ∗ ∗ --> a 3 {\displaystyle a_{14}*a_{3}} = ( r 1 ) 2 {\displaystyle (r_{1})^{2}}

a 5 ∗ ∗ --> b 4 {\displaystyle a_{5}*b_{4}} = ( d 1 ) 2 {\displaystyle (d_{1})^{2}}

a 8 ∗ ∗ --> b 6 {\displaystyle a_{8}*b_{6}} = a 9 ∗ ∗ --> b 7 {\displaystyle a_{9}*b_{7}} = ( r 1 ) 2 {\displaystyle =(r_{1})^{2}}

( b 14 ∗ ∗ --> c 14 ) ∗ ∗ --> ( a 15 + c 15 ) {\displaystyle (b_{14}*c_{14})*(a_{15}+c_{15})} = ( r 1 ) 2 {\displaystyle (r_{1})^{2}}

c 6 ∗ ∗ --> c 8 {\displaystyle c_{6}*c_{8}} = c 7 ∗ ∗ --> c 9 ) {\displaystyle c_{7}*c_{9})} = a 13 ∗ ∗ --> b 13 {\displaystyle a_{13}*b_{13}}

五和五较

a 2 + b 2 + c 2 = b 1 + c 1 {\displaystyle a_{2}+b_{2}+c_{2}=b_{1}+c_{1}}

a 3 + b 3 + c 3 = a 1 + c 1 {\displaystyle a_{3}+b_{3}+c_{3}=a_{1}+c_{1}}

a 4 + b 4 + c 4 = 2 b 1 {\displaystyle a_{4}+b_{4}+c_{4}=2b_{1}}

a 5 + b 5 + c 5 = 2 a 1 {\displaystyle a_{5}+b_{5}+c_{5}=2a_{1}}

a 6 + b 6 + c 6 = b 1 {\displaystyle a_{6}+b_{6}+c_{6}=b_{1}}

a 7 + b 7 + c 7 = b 1 {\displaystyle a_{7}+b_{7}+c_{7}=b_{1}}

a 8 + b 8 + c 8 = a 1 {\displaystyle a_{8}+b_{8}+c_{8}=a_{1}}

a 9 + b 9 + c 9 = a 1 {\displaystyle a_{9}+b_{9}+c_{9}=a_{1}}

a 10 + b 10 + c 10 = b 1 + c 1 − − --> a 1 {\displaystyle a_{10}+b_{10}+c_{10}=b_{1}+c_{1}-a_{1}}

a 11 + b 11 + c 11 = c 1 − − --> b 1 + a 1 {\displaystyle a_{11}+b_{11}+c_{11}=c_{1}-b_{1}+a_{1}}

a 12 + b 12 + c 12 = c 1 {\displaystyle a_{12}+b_{12}+c_{12}=c_{1}}

a 13 + b 13 + c 13 = a 1 + b 1 − − --> c 1 {\displaystyle a_{13}+b_{13}+c_{13}=a_{1}+b_{1}-c_{1}}

a 14 + b 14 + c 14 = c 1 − − --> a 1 {\displaystyle a_{14}+b_{14}+c_{14}=c_{1}-a_{1}}

a 15 + b 15 + c 15 = c 1 − − --> c 1 {\displaystyle a_{15}+b_{15}+c_{15}=c_{1}-c_{1}}

此外还有诸弦，大小差，诸差，诸率互见，四位拾遗，拾遗。

一共692关系式，这些关系式完全是几何定理，与具体数值无关。

举例：第三条中“勾股和即弦黄和”一句就是：三角形两直角边之和等于斜边加上内切圆直径（“黄”指内切圆直径）。这个命题可以由直角三角形的勾股定理推出：

后面出现的各问题，都根据这些公式中的相等关系而列出方程，然后求解。

李冶的692个公式中，有8个是错误的，只是因为数值吻合而被误认为成立。

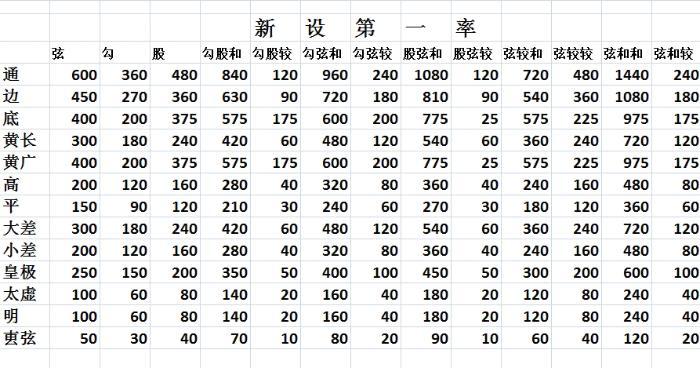
新设第一率

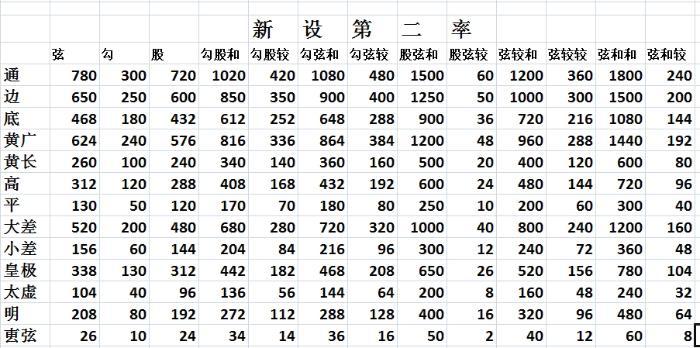
新设第二率

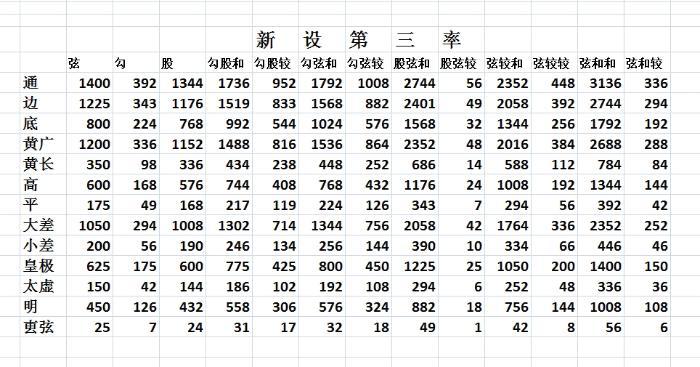
新设第三率

新设第四率

第二卷

测圆海镜卷二 正率

从第二卷开始，《测圆海镜》中一共出现了一百七十个问题，它们都是围绕着同一个题设背景而展开。 在第二卷开头，李冶作出了以后题目公用的总假设：

这里的圆城就是指 天地干 三角形的内切圆，其方向按照圆城图式里面 东南西北 四个点的位置而定（注意北在下方，东在左边，与现在通用的方位相反），所谓的“干地”、“坤地”则是指圆城图式里面出现的 干 点、 坤 点等等。以后的每个问题中要求的长度都是圆城的半径或直径。

接下来的问题都是已知某些线段的长度，问圆城的半径或直径。李冶在每一题的题目之后都先写出解法（代数演算），再给出演草（代入数值的计算）。

开头十个问题，不需要天元方程。清代数学李善兰认为，第一个问题和《九章算术》的勾股容圆题目一样，第二问至第十问就是《自序》中提到的“洞渊九容” 。但李冶原书或《四库全书》 李锐 较本都没有这九个问题的细草，李善兰在《天算或问》一书中根据相似三角形原理求得各式，并以第二问为例阐明如下 ：

又因：

所以

其余类推。 。

勾股容圆 d = 2 a 1 × × --> b 1 a 1 + b 1 + c 1 {\displaystyle d={2a_{1}\times b_{1} \over a_{1}+b_{1}+c_{1}}}

2 a 2 × × --> b 2 a 2 + b 2 + c 2 = d {\displaystyle {2a_{2}\times b_{2} \over a_{2}+b_{2}+c_{2}}=d}

2 a 3 × × --> b 3 a 3 + b 3 + c 3 = d {\displaystyle {2a_{3}\times b_{3} \over a_{3}+b_{3}+c_{3}}=d}

2 a 12 × × --> b 12 c 12 = d {\displaystyle {2a_{12}\times b_{12} \over c_{12}}=d}

2 a × × --> b a + b = d {\displaystyle {2a\times b \over a+b}=d}

2 a 10 × × --> b 10 b 10 − − --> a 10 + c 10 = d {\displaystyle {2a_{10}\times b_{10} \over b_{10}-a_{10}+c_{10}}=d}

2 a 11 × × --> b 11 b 11 − − --> a 11 + c 11 = d {\displaystyle {2a_{11}\times b_{11} \over b_{11}-a_{11}+c_{11}}=d}

2 a 13 × × --> b 13 b 13 + a 13 − − --> c 13 = d {\displaystyle {2a_{13}\times b_{13} \over b_{13}+a_{13}-c_{13}}=d}

2 a 14 × × --> b 14 c 14 − − --> a 14 = d {\displaystyle {2a_{14}\times b_{14} \over c_{14}-a_{14}}=d}

2 a 15 × × --> b 15 c 15 − − --> b 15 = d {\displaystyle {2a_{15}\times b_{15} \over c_{15}-b_{15}}=d}

测圆海镜细草 卷二 第十四问 草曰

从第十四题开始，引入 天元术 ，将所求的未知量设为“ 天元 ”，然后根据 识别杂记 中给出的公式构造出两个天元式，另其相等，然后解方程得出答案。《测圆海镜》中天元式的次序，高次幂在常数项之上，和《益古演段》，《四元玉鉴》的相反。

“或问出西门南行四百八十步有树，出北门东行二百步见之。问答同前”。

内减天元半径得股圆差： 480 − − --> x {\displaystyle 480-x}

又置乙东行步在地，内减天元，得勾圆差： 200 − − --> x {\displaystyle 200-x}

以勾圆差增乘股圆差得半段黄方幂： x 2 − − --> 680 x + 96000 {\displaystyle x^{2}-680x+96000}

又置天元幂以倍之，也为半段黄方幂；

因此，得 x 2 − − --> 680 x + 96000 = 2 x 2 {\displaystyle x^{2}-680x+96000=2x^{2}}

相消得： − − --> x 2 − − --> 680 x + 96000 = 0 {\displaystyle -x^{2}-680x+96000=0}

解方程，得半径 r = 120 {\displaystyle r=120} 。

第三卷

第四卷

。

第三卷边股问与第四卷同次第底勾问成对偶。

第五卷

大股18问：已知 b 1 {\displaystyle b_{1}} 。

第六卷

大勾18问：

第七卷

明叀前18问；求直径d。

第八卷

第十四问

草曰：

已知

9604 ∗ ∗ --> x 2 + 1546244 ∗ ∗ --> x − − --> 138297600 = 0 {\displaystyle 9604*x^{2}+1546244*x-138297600=0}

第九卷上

：大斜四问

第九卷下

：大和8问

第十卷

：三事和8问

第十一卷

第十七问，十八问取自《洞渊算书》。

第十二卷

版本

天元术并非李冶的独创，而是从金代起便在中国北方开始萌芽。据祖颐在《四元玉鉴后序》中的记载，李冶以前研究天元术的学者有北宋蒋周撰《益古集》、李文一撰《照胆》，石信道撰《钤经》、刘汝谐撰《如积释锁》等书，世人才知道有天元。此外朱世杰《四元玉鉴》引用北宋《洞渊九容细草》两道题，其中有“立天元一” 。后来李德载撰《两仪群英集臻》兼有地元。1306年元刻本《阴阳备用三元节要》三卷下有天元，地元 。但是这些早期天元术的著作已经失传。宋代《杨辉算法》保留蒋周《益古集》的一些条段法的题目，没保留天元术的内容。现存元刻本《阴阳备用三元节要》只有一条二元术题，《测圆海镜》是现存最早的系统地讲述天元术的著作。

到了明代，天元术因为艰深难懂而少人研究，几近失传。明代唐顺抄录过《测圆海镜》，但不懂天元术；顾应祥曾经撰写《测圆海镜分类释术》，但完全没有明白天元术中天元为未知数的含义，因而将《测圆海镜》中关于立天元列方程的演算全部删去，只留下用开方术解方程的过程，以便后人学习 。李俨认为宋金元发展起来的天元术至此已被遗忘 。《测圆海镜分类释术》一书，虽然删除了天元术内容，但保存了全部算题，也补入正确的几何学解法，使得几近失传的《测圆海镜》，得以从新流传 。

十八世纪时，随着西洋算学传入中国，李冶等人的天元术著作才被后来的数学家重新发现。戴东原从《永乐大典》中辑录出李冶《测圆海镜》 ；清朝梅瑴成（梅文鼎之孙）曾经研读元学士李冶的《测圆海镜》，对其中的天元之术感到不解，后来在研习西方的“借根方”法时发现所谓的“借根”就是“立天元”（都是设未知数），方才重新开始认识天元术 。之后，《四元玉鉴》等其它天元术著作也被重新认识。孔广森曾校对《测圆海镜》中的四章。乾隆三十八年（1773年），《四库全书》收录了李潢家藏本的《测圆海镜》。1798年，清代大藏书家鲍廷博刊印的《知不足斋丛书》中收录了 李锐 校勘的《测圆海镜细草》十二卷 。之后又有焦循和 李锐 在研究了《测圆海镜》、《益古演段》和《数书九章》后写的《天元一释》和《开方通释》两书，用较为明白的语言详细解释了李冶的天元术和秦九韶的正负开方术。1873年，张楚钟发表《测圆海镜通释》对《识别杂记》中的几百条定理，用几何方法逐条证明。

清代研究

1896年刘岳云出版《测圆海镜解》，发现《圆城图式》中各线段的简单加减关系，发表《诸率加减表》，此后李善兰出版《测圆海镜解》等 。他在另一篇著作《天算或问》中给出勾股容圆各公式的统一公式。其后陈维祺发表《各率及较泛积表》将《识别杂记》用“泛积”概念统一表示 。王季同在《九容公式》中进一步发展了陈维祺的成果，发现

国际研究

19世纪初，朝鲜数学家南秉哲著《海镜细草解》。

1913年，法国学者L.van Hoe 介绍《测圆海镜》。1982年，法国林力娜（K. Chemla)作论文 Etude du Livre Reflects des Mesuers du Cercle sur la mer de Li Ye，获得博士学位。1983年，新加坡大学教授蓝丽蓉发表 Chinese Polynomial Equations in the Thirteenth Century,论述《测圆海镜》。

评价

清代数学家对《测圆海镜》给予很高评价。阮元认为《测圆海镜》是“中土数学之宝书”，李善兰称赞它是“中华算书，无有胜于此者”。白尚恕说，《测圆海镜》的成就，超过同时期的印度，阿拉伯和欧洲，“处于世界数学里遥遥领先的地位”

参考文献

来源

李人言. 《中国算学史》. 台湾商务印书馆. 1965.

孔国平. 《李冶朱世杰与金元数学》. 河北科学技术出版社. 2000. ISBN 978-7-537-51884-0.

参见

李冶《益古演段》

朱世杰《四元玉鉴》

李善兰

秦九韶算法

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。