重差理论的历史

重差理论起源于《周髀算经》的《日高图》“以表高乘两表相去为黄甲之实。以影差为黄乙之广而一，所得则变为黄乙之袤，上与日齐。”

刘徽在《九章算术·序》中，进一步发展了重差术：“凡望极高、测绝深，而兼知其远者必用重差、句股，则必以重差为率，故曰 重差 也。立两表于洛阳之城，令高八尺。南北各尽平地，同日度其正中之时，以景差为法，表高乘表间为实，实如法而一。所得加表高，即日去地也。以南表之景乘表间为实，实如法而一，即为从南表至南戴日下也。以南戴日下及日去地为句、股，为之求弦，即日去人也。”

内容

《海岛算经》共九问。都是用表尺重复从不同位置测望，取测量所得的差数，进行计算从而求得山高或谷深，这就是刘徽的重差理论。《海岛算经》中，从题目文字可知所有计算都是用筹算进行的。“为实”指作为一个分数的分子，“为法”指作为分数的分母。所用的长度单位有里、丈、步、尺、寸；１里＝180丈=1800尺；1丈=10尺：1步=6尺，1尺=10寸。

望海岛

今有望海岛，立两表，齐高三丈，前后相去千步，令后表与前表三相直。从前表却行一百二十三步，人目着地取望岛峰，与表末三合。从后表却行一百二十七步，人目着地取望岛峰，亦与表末三合。问岛高及去表各几何？ 答曰：岛高四里五十五步；去表一百二里一百五十步。 术曰：以表高乘表间为实；相多为法，除之。所得加表高，即得岛高。求前表去岛远近者：以前表却行乘表间为实；相多为法。除之，得岛去表里数。

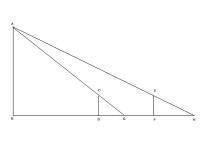
望海岛二次测量示意图

由于前表去岛的距离不能直接测量，刘徽用同样高度的表杆前后测量，表杆与地面垂直，人眼贴地，望表杆顶和岛上山顶对齐，这时测得人眼和前表杆的水平距离叫“前表却行”DG=123步；再将表杆往后移动，两表杆间距称为“表间”=1000步，依法测出“后表却行”FH=127步。

依法得岛高 AB= C D × × --> D F F H − − --> D G + C D {\displaystyle {\tfrac {CD\times DF}{FH-DG}}+CD}

依法得前表去岛远近 BD= D G × × --> D F F H − − --> D G {\displaystyle {\tfrac {DG\times DF}{FH-DG}}}

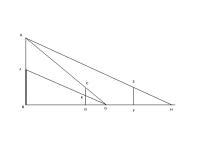
松生山上三次测量示意图

望松生山上

今有望松生山上，不知高下。立两表齐，高二丈，前后相去五十步，令后表与前表三相直。从前表却行七步四尺，薄地遥望松末，与表端三合。又望松本，入表二尺八寸。复从后表却行八步五尺，薄地遥望松末，亦与表端三合。问松高及山去表各几何？ 答曰：松高一十二丈二尺八寸；山去表一里二十八步、七分步之四。术曰：以入表乘表间为实。相多为法，除之。加入表，即得松高。求表去山远近者：置表间，以前表却行乘之为实。相多为法，除之，得山去表。

CD EF 表示前后两支表杆，前表杆有刻度，用作两次测量，第一次从G点瞄准A、C两点成直线，第二次从G点校准树根J，读出前表杆上度数（入表）。

松高=AJ= C K × × --> D F ( F H − − --> D G ) + C K {\displaystyle {\tfrac {CK\times DF}{(FH-DG)}}+CK}

前表去山远近=BD= D F × × --> D G ( F H − − --> D G ) {\displaystyle {\tfrac {DF\times DG}{(FH-DG)}}}

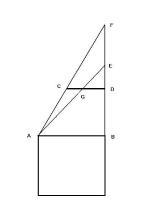
《海岛算经》今有南望方邑示意图

南望方邑

今有南望方邑，不知大小。立两表东、西去六丈，齐人目，以索连之。令东表与邑东南隅及东北隅三相直。当东表之北却行五步，遥望邑西北隅，入索东端二丈二尺六寸半。又却北行去表一十三步二尺，遥望邑西北隅，适与西表相三合。问邑方及邑去表各几何？ 答曰：邑方三里四十三步、四分步之三；邑去表四里四十五步。 术曰：以入索乘后去表，以两表相去除之，所得为景差；以前去表减之，不尽以为法。置后去表，以前去表减之，余以乘入索为实。实如法而一，得邑方。求去表远近者：置后去表，以景差减之，余以乘前去表为实。实如法而一，得邑去表。

由于待测的方城宽度AB，在东西方向，与地面平行，因此两支在C点D点插入地面与地面垂直的表杆，在此不用作直接测量，测量是依靠一根拴在C、D两根垂直表杆中间的一条水平测量绳索CD完成的。此题中一根水平测量绳作两次测量用。

望深谷

今有望深谷，偃矩岸上，令勾高六尺。从勾端望谷底，入下股九尺一寸。又设重矩于上，其矩间相去三丈。更从勾端望谷底，入上股八尺五寸。问谷深几何？答曰：四十一丈九尺。术曰：置矩间，以上股乘之，为实。上、下股相减，余为法，除之。所得以勾高减之，即得谷深。

登山望楼

今有登山望楼，楼在平地。偃矩山上，令句高六尺。从句端斜望楼足，入下股一丈二尺。又设重矩于上，令其间相去三丈。更从句端斜望楼足，入上股一丈一尺四寸。又立小表于入股之会，复从句端斜望楼岑端，入小表八寸。问楼高几何？ 答曰：八丈。 术曰：上下股相减，余为法；置矩闲，以下股乘之，如句高而一。所得，以入小表乘之，为实。实如法而一，即是楼高。 楼高=（距间 * 下股）* （入小表）/句高/（下股-上股）。

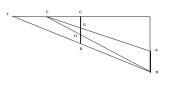
《海岛算经》东南望波口示意图

南望波口

今有东南望波口，立两表南、北相去九丈，以索薄地连之。当北表之西却行去表六丈，薄地遥望波口南岸，入索北端四丈二寸。以望北岸，入前所望表里一丈二尺。又却后行1去表一十三丈五尺。薄地遥望波口南岸，与南表三合。问波口广几何？答曰：一里二百步。 术曰：以后去表乘入索，如表相去而一。所得，以前去表减之，余以为法；复以前去表减后去表，余以乘入所望表里为实，实如法而一，得波口广。

此题中一根水平测量绳，作三次测量用。

望清渊

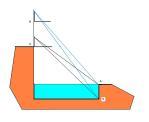
望清渊示意图

今有望清渊，渊下有白石。偃矩岸上，令句高三尺。斜望水岸，入下股四尺五寸。望白石，入下股二尺四寸。又设重矩于上，其间相去四尺。更从句端斜望水岸，入上股四尺。以望白石，入上股二尺二寸。问水深几何？ 答曰：一丈二尺。 术曰：置望水上下股相减，余以乘望石上股为上率。又以望石上下股相减，余以乘望水上股为下率。两率相减，余以乘矩间为实；以二差相乘为法。实如法而一，得水深。又术：列望水上下股及望石上下股，相减，余为法。以望石下股减望水下股，余以乘矩间为实，实如法而一，得水深。

A标志水岸，S标志白石，C标志岸边；句是古代测量用具之一，有两个边成直角（如今三角板）：使用时句的一边务必与地面垂直。此题用两个句，一个在C，一个在D，各测量水岸和水底白石。此题用四次测望术。

登山望津

今有登山望津，津在山南。偃矩山上，令句高一丈二尺。从句端斜望津南岸，入下股二丈三尺一寸。又望津北岸，入前望股里一丈八寸。更登高岩北，却行二十二步，上登五十一步，偃矩山上。更从句端斜望津南岸，入上股二丈二尺。问津广几何？ 答曰：二里一百二步。 术曰：以句高乘下股，如上股而一。所得以句高减之，余为法；置北行，以句高乘之，如上股而一。所得以减上登，余以乘入股里为实。实 如法而一，即得津广。

登山临邑

今有登山临邑，邑在山南。偃矩山上，令勾高三尺五寸。令勾端与邑东南隅及东北隅三相直。从勾端遥望东北隅，入下股一丈二尺。又施横勾于入股之会，从立勾端望西北隅，入横勾五尺。望东南隅，入下股一丈八尺。又设重矩于上，令矩间相去四丈。更从立勾端望东南隅，入上股一丈七尺五寸。问邑广长各几何？ 答曰：南北长一里一百步；东西广一里三十三步、少半步。术曰：以勾高乘东南隅入下股，如上股而一，所得减勾高，余为法；以东北隅下股减东南隅下股，余以乘矩间为实。实如法而一，得邑南北长也。求邑广：以入横勾乘矩间为实。实如法而一，即得邑东西广。

此题用四次测望术

历代研究

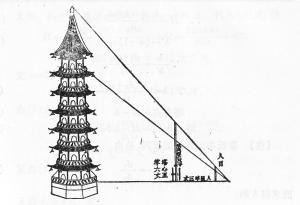
秦九韶 《数书九章》《表望浮屠》

南北朝数学家祖冲之曾为《九章重差图》作注。唐朝将《九章重差图》从《刘徽九章算术注》中分离出来单独成书，以第一题“今有望海岛”取名为《海岛算经》。唐高宗显庆元年（656年）数学家李淳风等注释《算经十书》，作为国子监学习和考试用书，《海岛算经》就是《算经十书》之一，并且规定《海岛算经》的学习期限为三年，是其他算经学习期限的三倍 ，可见《海岛算经》在唐代受重视的程度。北宋元丰七年（1084年）和南宋宁宗嘉定六年（1213年）先后刻印两次。但宋刻本《海岛算经》后来遗失。南宋秦九韶研究过类似于海岛算经的测量书题目《表望浮屠》，南宋数学家杨辉《续古摘奇算法》讨论了四种测量问题，包括来自《海岛算经》海岛题，并指出“登高望松，遥望波口，非三望之术乎？清渊白石、登山临邑，非四望之术乎？”。明永乐年间收入《永乐大典》，但只存刘徽文字和李淳风注，刘徽原图和刘徽所作的注释已不存。元朝数学家朱世杰《四元玉鉴》《勾股测望》门第四，六，七，八等四问用天元术阐述《海岛算经》的《望海岛》，《望深谷》，《南望方邑》，《望清渊》。清乾隆时代，经学家戴震将《海岛算经》文字，从《永乐大典》中辑录出来收入《四库全书》 。 清代数学家李潢著《海岛算经细草图说》，沈钦裴著《重差图说》，均以欧几里德几何学论证，已失刘徽原意 。 李镠著《海岛算经纬笔》。到民国时期，中算史家李俨《重差术流源及其新注》 和《中国古代中算家的测绘术》 ，《海岛算经新注》 都对《海岛算经》有所论述。

近年中国数学家白尚恕 对海岛算经有较详细的论证。吴文俊院士论文《我国古代测望之学重差理论评介兼评数学史研究中的某些方法问题》 与《海岛算经古证探源》 两篇论文对《海岛算经》有详细的论证，前文批评一些前人对《海岛算经》的论证中添加欧几里德几何的平行线或利用相似形理论或后代的代数论证的方法，颠倒历史，都是错误的方法，并提出正确的论证，必须以刘徽时代的出入相补原理为基础，才能还原《海岛算经》的。

传播

《海岛算经》在唐代传入朝鲜、日本。最早向西方介绍《海岛算经》的是19世纪来华传教士伟烈亚力。他1852年在《北华捷报》（North China Herald，《字林西报》前身）发表的论文：《中国数学科学札记》（Jottings on the Sciences of Chinese Mathematics）。伟烈亚力在文中介绍了《海岛算经》，说此书是“一部关于实用三角学的九个问题”。1913年日本数学史家三上义夫在其英文著作《中国与日本数学的发展》 第五章《海岛算经》 中译出头三则问题，1932年法国数学家 L·van·Hee 翻译《海岛算经》全文 。1986年澳大利亚华人数学家洪天赐和美国数学家弗兰克·斯委特兹将《海岛算经》全文翻译成英文。此外还有日文翻译本和俄文翻译本。

评价

3世纪刘徽《海岛算经》运用二次、三次、四次测望法，是测量学历史上领先的创造。中外学者对《海岛算经》的成就，给予很高的评价。《海岛算经》的英译者和研究者，美国数学家弗兰克·斯委特兹，在比较西欧测量学从古代希腊、罗马直到文艺复兴时期的发展，认为希腊测量术，重点在测量器具的运用，而其数学水准远不如刘徽《海岛算经》，直到文艺复兴时代，才差强达到《海岛算经》水准。他还指出17世纪初意大利来华传教士利玛窦和中国徐光启合著的《测量法义》十五题，并未能达到或超越《海岛算经》。他结论；“简而言之，在测量数学领域，中国人的成就，超越西方世界约一千年。 ”

《中国数学大系》一书中评价《海岛算经》：“使中国测量学达到登峰造极的地步。在西欧直到16，17世纪，才出现二次测量术的记载，到18世纪，才有了三、四次测量之术，可见中国古代测量学的意境之深，功用之广” 。刘徽《海岛算经》的测量术，实比欧洲早一千三百至一千五百年。

翻译本

（法）L. van Hee: Le Classique de l"Île Maritime: Ouvrage Chinois de III siècle 1932。

（美）Frank J. Swetz: The Sea Island Mathematical Manual, The Pennsylvania State University Press, 1992 ISBN 0-271-00799-0

（日）川原秀成译 《海岛算经》

（俄）别辽姿金娜译 《海岛算经》 1974年

参考文献

^ 引自吴文俊主编 《中国数学史大系》第三卷 248页 ISBN 7-303-04557-0/O

^ "Quite Simply, in the endeavors of mathematical surveying, China"s accomplishments exceeded those realized in the West by about one thousand years", 见 弗兰克·斯委特兹: 《海岛算经:古代中国的测量学和数学》第四章第二节 比较回顾： 中国测量学的成就。（Frank J. Swetz: The Sea Island Mathematical Manual,Surveying and Mathematics in Ancient China 4.2 Chinese Surveying Accomplishments, A Comparative Retrospection 第63页 The Pennsylvania State University Press, 1992 ISBN 0-271-00799-0 ）

^ 关于此题的讨论详见吴文俊主编 《中国数学大系》第三卷 247-248 ISBN 7-303-04557-0/O

^ Frank J. Swetz: The Sea Island Mathematical Manual, P9 The Pennsylvania State University Press, 1992 ISBN 0-271-00799-0

^ Frank J. Swetz: The Sea Island Mathematical Manual, P13 The Pennsylvania State University Press, 1992 ISBN 0-271-00799-0

^ 吴文俊 《我国古代测望之学重差理论评介兼评数学史研究中的某些方法问题》 《吴文俊文集》 12-73 山东教育出版社 1986

^ 李俨《[重差术流源及其新注》《李俨.钱宝琮科学史全集》卷10

^ 李俨《中国古代中算家的测绘术》《李俨.钱宝琮科学史全集》卷10

^ 李俨 《海岛算经新注》 《中国古代数学史料》 中国科学图书仪器公司 1954

^ 白尚恕 《刘徽海岛算经造术的探讨》 《白尚恕文集 中国数学史研究》 73-82 北京师范大学出版社 2008 ISBN 978-7-303-09242-0

^ 吴文俊 《我国古代测望之学重差理论评介兼评数学史研究中的某些方法问题》 《吴文俊文集》 12-73 山东教育出版社 1986

^ 吴文俊 《海岛算经古证探源》 《吴文俊文集》 54-72

^ Mikami, Yoshio: The Development of Mathematics in China and Japan 1913

^ L. van Hee: Le Classique de l"Île Maritime: Ouvrage Chinois de III siècle 1932

^ Frank J. Swetz: The Sea Island Mathematical Manual, The Pennsylvania State University Press, p63 1992 ISBN 0-271-00799-0

^ 引自吴文俊主编 《中国数学大系》第三卷 东汉三国 243-248 ISBN 7-303-04557-0/O

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。