简单应用

圆柱体

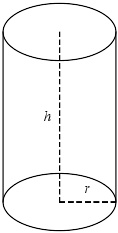
圆柱体

如果垂直转轴切开圆柱体，设r{\displaystyle r}为半径，可以得到横切面面积为π π -->r2{\displaystyle \pi r^{2}}的圆形。根据祖暅原理，圆柱体的体积相等于底面积相等于圆面积π π -->r2{\displaystyle \pi r^{2}}、高为h{\displaystyle h}的长方体，所以半径为r{\displaystyle r}和高为h{\displaystyle h}的圆柱体体积是π π -->r2⋅ ⋅ -->h{\displaystyle \pi r^{2}\cdot h}。

半球体

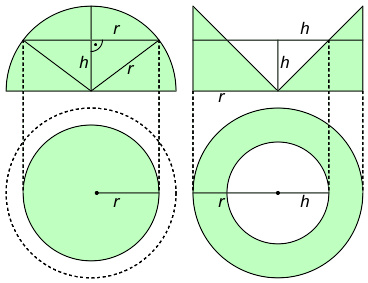
垂直（上）以及水平（下）切开半球体和对照立体

从其中一层以垂直表面的高h{\displaystyle h}横切半径为r{\displaystyle r}的半球体，根据勾股定理，半径为：

所以横切面面积是：

对照立体是一个拥有与半球体相同横切面积和高的立体，中间有一个圆锥体。高h{\displaystyle h}的对照立体环形切面有内圆周r{\displaystyle r}以及外圆周h{\displaystyle h}，其面积如下：

因此两个立体都满足祖暅原理并且有相同体积。对照立体的体积便是圆柱体和圆锥体体积之差，所以

成功利用这条有名的方程计算出半球体体积，从而导出球体体积公式。

微积分

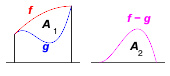
两条方程式积分后的差与两条方程式之差的积分

祖暅原理背后的概念经常出现在微积分中。作为维度的一个例子，因此两条方程式在两个交点间的面积可以利用以下方程获得：

实质上表示了函数图形f{\displaystyle f}和g{\displaystyle g}之间的A1{\displaystyle A_{1}}面积与函数图形x↦ ↦ -->f(x)− − -->g(x){\displaystyle x\mapsto f(x)-g(x)}下的A2{\displaystyle A_{2}}相同，而后者的交点距离与前者相等。由于现代数学中的积分和面积的互相关系，而体积可以通过微分计算，使祖暅原理变得更为少用。

参考文献

（英文）伽利略计划：卡瓦列里

（英文）

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。