正式定义

一个纤维丛由四元组（E, B, π, F）组成，其中E, B, F　是拓扑空间而π : E → B　是一个连续满射，满足下面给出的局部平凡（local triviality）条件。B 称为丛的基空间（base space），E 称为总空间（total space）,而F 称为纤维（fiber）。映射π 称为投影映射.下面我们假定基空间B 是连通的。

我们要求对于B 中的每个点 x,存在一个在 B 中 包含 x 的开邻域U，并有一个同胚映射 φ:π（U）→ U × F (显然　U × F　是一个乘积空间) ，φ 并且要满足 π π -->(y)=proj1∘ ∘ -->φ φ -->(y),∀ ∀ -->y∈ ∈ -->π π -->− − -->1(U){\displaystyle \textstyle \pi (y)=\operatorname {proj} _{1}\circ \varphi (y),\,\forall y\in \pi ^{-1}(U)}，也就是下图是可交换的：

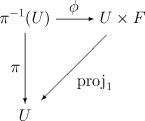
其中 proj1 : U × F → U 是自然投影而 φ : π(U) → U × F 是一个同胚（这里的局部平凡条件有些书会定义为 x=π π -->∘ ∘ -->φ φ -->− − -->1(x,f),∀ ∀ -->x∈ ∈ -->U,f∈ ∈ -->F{\displaystyle \textstyle x=\pi \circ \varphi ^{-1}(x,f),\,\forall x\in U,f\in F}）。所有{(Ui, φi)} 的集合称为丛的局部平凡化。

对于 B 中每点 p，原象（preimage）π(p) 和 F 同胚并称为点 p 上的纤维.一个纤维丛（E, B, π, F）经常记为

以引入一个空间的短恰当序列。注意每个纤维丛 π : E → B 都是一个开映射，因为积空间的投影是开映射。所以 B 有由映射π决定的商拓扑(quotient topology).

一个光滑纤维丛是一个在光滑流形的范畴内的纤维丛。也就是，E, B, F都必须是光滑流形且所有上面用到的函数都必须是光滑映射。

例子

令E = B × F并令π : E → B为对第一个因子的投影，则E是B上的丛.这里E不仅是局部的积而且是整体的积。任何这样的纤维丛称为平凡丛.

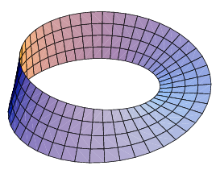
莫比乌斯带是圆上的非平凡丛。

最简单的非平凡丛的例子可能要算莫比乌斯带（Möbius strip）.莫比乌斯带是一个以圆为基空间B并以线段为纤维F的丛。对于一点x∈ ∈ -->B{\displaystyle x\in B}的邻域是一段圆弧；在图中，就是其中一个方块的长。原象π π -->− − -->1(U){\displaystyle \pi ^{-1}(U)}在图中是个（有些扭转的）切片，4个方块宽一个方块长。同胚φ把U的原象映到柱面的一块：弯曲但不扭转.

相应的平凡丛B × F看起来像一个圆柱，但是莫比乌斯带有个整体上的扭转。注意这个扭转只有整体上才能看出来；局部看来莫比乌斯带和圆柱完全一样（在其中任何一个竖直的切一刀会产生同样的空间）。

一个类似的非平凡丛是克莱因瓶，它可以看作是一个"扭转"的圆在另一个圆上的丛。相应的平凡丛是一个环，S × S。

一个覆盖空间是一个以离散空间为纤维的纤维丛。

纤维丛的一个特例，叫做向量丛,是那些纤维为向量空间的丛（要成为一个向量丛，丛的结构群—见下面—必须是一个线性群）。向量丛的重要实例包括光滑流形的切丛和余切丛。

另一个纤维丛的特例叫做主丛。更多的例子参看该条目。

一个球丛是一个纤维为n维球面的纤维丛。给定一个有度量的向量丛（例如黎曼流形的切丛），可以构造一个相应的单位球丛,其在一点x的纤维是所有Ex的单位向量的集合.

截面

纤维丛的截面（section或者cross section）是一个连续映射f : B → E使得π(f(x))=x对于所有B中的x成立。因为丛通常没有全局有定义的截面，理论的一个重要作用就是检验和证明他们的存在性。这导致了代数拓扑的示性类理论。

截面经常只被局部的定义（特别是当全局截面不存在时）。纤维丛的局部截面是一个连续映射f : U → E其中U是一个B中的开集而π(f(x))=x对所有U中的x成立。若（U, φ）是一个局部平凡化图，则局部截面在 U上总是存在的。这种截面和连续映射U → F有1-1对应。截面的集合组成一个层（sheaf）。

结构群和转移函数

纤维丛经常有一个对称群描述重叠的图之间的相容条件。特别的，令G为一个拓扑群，它连续的从左边作用在纤维空间F上。不失一般性的，我们可以要求G有效的作用在F上，以便把它看成是F的同胚群。纤维丛的一个G-图册（E, B, π, F）是之前定义过的局部平凡化并且满足：对任何两个重叠的局部平凡化中的元素也就是图（Ui, φi）和（Uj, φj）且 Ui∩ ∩ -->Uj≠ ≠ -->∅ ∅ -->{\displaystyle U_{i}\cap U_{j}\neq \emptyset }，则函数

是由以下方式给出：

其中 tij:Ui∩ ∩ -->Uj→ → -->G{\displaystyle t_{ij}:U_{i}\cap U_{j}\to G} 是一个称为转移函数（transition function）的连续映射。两个G-图册是等价的如果他们的并集也是G-图册。一个G-丛是有G-图册等价类的纤维丛。群G称为该丛的结构群（structure group）。

在光滑范畴中，一个G-丛是一个光滑纤维丛，其中G是一个李群而相应的在F上的作用是光滑的并且变换函数都是光滑映射。

转移函数tij满足以下条件

tii(x)=1{\displaystyle t_{ii}(x)=1}

tij(x)=tji(x)− − -->1{\displaystyle t_{ij}(x)=t_{ji}(x)^{-1}}

tik(x)=tij(x)tjk(x){\displaystyle t_{ik}(x)=t_{ij}(x)t_{jk}(x)}

第三个条件用到三个相交的 Ui∩ ∩ -->Uj∩ ∩ -->Uk{\displaystyle U_{i}\cap U_{j}\cap U_{k}}上叫做上链条件（cocycle condition，见Čech上同调）。

一个主丛是一个G-丛，其纤维可以认为是G本身，并且有一个在全空间上的G的右作用保持纤维不变。

参见

向量丛

主丛

拉回丛（pullback bundle）

纤维化

覆盖映射

规范场论

参考

Norman Steenrod, The Topology of Fiber Bundles, Princeton University Press (1951). ISBN 0-691-00548-6.

David Bleecker, Gauge Theory and Variational Principles, Addison-Wesley publishing, Reading, Mass (1981). ISBN 0-201-10096-7. See chapter one.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。