定义

设 n {\displaystyle n} 是一个正整数， r {\displaystyle r} 是正整数或 ∞ ∞ --> {\displaystyle \infty } ， I {\displaystyle I} 是实数非空区间， t {\displaystyle t} 属于 I {\displaystyle I} 。一个 C r {\displaystyle C^{r}} 类（即 γ γ --> {\displaystyle \gamma } 为 r {\displaystyle r} 次连续可微）向量值函数

称为一条 C r {\displaystyle C^{r}} 类参数曲线 或曲线 γ γ --> {\displaystyle \gamma } 的一个 C r {\displaystyle C^{r}} 参数化， t {\displaystyle t} 称为曲线 γ γ --> {\displaystyle \gamma } 的参数， γ γ --> ( I ) {\displaystyle \gamma (I)} 称为曲线的 像 。将曲线 γ γ --> {\displaystyle \gamma } 和曲线的像 γ γ --> ( I ) {\displaystyle \gamma (I)} 区别开来非常重要，曲线是一个映射，而像是一个集合。一个给定的像可以描述为许多不同的 C r {\displaystyle C^{r}} 曲线。

可以想象参数 t {\displaystyle t} 代表时间，而曲线 γ γ --> ( t ) {\displaystyle \gamma (t)} 作为空间中一个运轨迹子轨迹。

如果 I 是闭区间 [ a , b ]，我们称 γ( a ) 为曲线 γ 的 起点 而 γ( b ) 为 终点 。

如果 γ γ --> ( a ) = γ γ --> ( b ) {\displaystyle \gamma (a)=\gamma (b)} ，我们说 γ 是 闭的 或是一个 环路 。进一步，我们称 γ 是一条 闭 C -曲线 ，如果 γ (a) = γ ( b ) 对所有 k ≤ r 。

如果 γ γ --> : ( a , b ) → → --> R n {\displaystyle \gamma :(a,b)\to \mathbb {R} ^{n}} 为单射，我们称为 简单 曲线。

如果参数曲线 γ γ --> {\displaystyle \gamma } 局部可写成幂级数，我们称曲线 解析 或是 C ω ω --> {\displaystyle C^{\omega }} 类。

记号 - γ γ --> {\displaystyle \gamma } 表示朝相反的方向运动的曲线。

一条 C k {\displaystyle C^{k}} -曲线

称为 m {\displaystyle m} 阶正则 当且仅当对任何 t {\displaystyle t} 属于 I {\displaystyle I}

在 R n {\displaystyle \mathbb {R} ^{n}} 中线性无关。

特别地，一条 C 1 {\displaystyle C^{1}} -曲线 γ γ --> {\displaystyle \gamma } 是 正则 的如果

重新参数化与等价关系

给定一条曲线的像我们可以定义曲线的许多不同的参数化。微分几何旨在描述在一定的参数化下不变的性质。所以我们需在所有参数曲线集合上定义一种合适的等价关系。曲线的微分几何性质（长度，Frenet 标架和广义曲率）在重新参数化下不变从而满足等价类性质。这个等价类称为 C 曲线 ，是曲线的微分几何研究的中心。

两个 C 参数曲线

与

要称为 等价 ，就要存在一个 C 双射

使得

和

γ 2 称为 γ 1 的 重新参数化 。这种 γ 1 的重新参数化在所有参数 C 曲线的集合上定义了一种等价关系，其等价类称为 C 曲线 。

对 定向 C 曲线 ，我们可以定义一种“加细”的等价关系，要求 φ 满足 φ"( t ) > 0。

等价的 C 曲线有相同的像；等价的定向 C 曲线有相同的运动方向。

长度与自然参数化

C 曲线 γ : [ a , b ] → R 的长度 l 可以定义为

曲线的长度在重参数化下保持不变，从而是曲线的一个微分几何性质。

对任何正则 C （ r 至少为 1）曲线 γ: [ a , b ] → R 我们可以定义一个函数

写成

这里 t ( s ) 是 s ( t ) 的逆函数，我们得到 γ 的一个新参数化 γ γ --> ¯ ¯ --> {\displaystyle {\bar {\gamma }}} ，称为 自然 、 弧长 速度 单位速度 参数化；参数 s ( t ) 称为 γ 的 自然参数 。

我们偏爱这个参数，因为自然参数 s ( t ) 以单位速度转动 γ 的像，所以

在实际中常常很难计算出一条曲线的自然参数，但在理论讨论中很有用。

给定一条参数化曲线 γ( t ) 的自然参数化是在差一个参数移动的意义下是惟一的。

数量

经常称为曲线的 能量 或作用量；这个名称是有理由的，因为测地线方程是这个作用量的欧拉-拉格朗日运动方程。

Frenet 标架

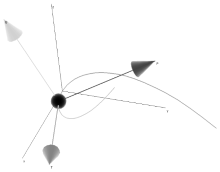
空间曲线一点的 Frenet 标架示意图。 T 是单位切向量， P 为单位法向量， B 是次法向量。

一个 Frenet 标架 是一个移动的参考标架，由描述曲线在每一点 γ( t ) 局部性质的 n 个正交向量 e i ( t ) 组成。这是微分几何处理曲线的主要工具，因为在这个局部参考系中，远比使用欧几里得那样的整体坐标系更容易和自然地描述局部性质（如曲率、挠率）。

给定 R 中一条 n 阶正则 C -曲线 γ，曲线的 Frenet 标架 是一组正交向量

称为 Frenet 向量 。它们是通过对 γ( t ) 的各阶导数使用格拉姆-施密特正交化算法得到的：

实值函数 χ i ( t ) 称为 广义曲率 ，定义为

Frenet 标架和广义曲率在重新参数化下是不变的，故它们是曲线的微分几何性质。

特殊 Frenet 向量和广义曲率

最初三个 Frenet 向量和广义曲率可以在三维空间中看到。它们有额外的名字以及与名称相关更多信息。

切向量

如果曲线 γ 表示一个质点的轨迹，那么质点在给定点 P 的瞬时速度用一个向量表示，称为曲线在 P 的 切向量 。

数学表述为，给定一条曲线 γ = γ( t )，对参数 t 的任何值： t = t 0 ， 向量：

是点 P = γ( t 0 ) 的切向量。一般说，切向量可以为零向量。

切向量的长度：

是在时间 t 0 的速率。

第一个 Frenet 向量 e 1 ( t ) 是在同一方向的 单位切向量 ，在 γ 的每个正则点有定义：

如果 t = s 是自然参数则切向量有单位长，从而公式化简为：

单位切向量确定了曲线的 定向 ，或随着参数增长的前进方向。

法向量

法向量 ，有时也称为 曲率向量 ，表明曲线和一条直线的偏离程度。

法向量定义为

其正规形式 单位法向量 ，是 Frenet 向量 e 2 ( t )，定义为

t 点的切向量和法向量张成 t 点的 密切平面 。

曲率

第一个广义曲率 χ 1 ( t ) 称为 曲率 ，度量了曲线 γ 偏离密切平面上一条直线的程度。定义为

称为 γ 在点 t 的曲率。

曲率的倒数

称为 曲率半径 。

半径为 r 的圆周有常曲率

但一条直线的曲率是 0 。

次法向量

次法向量 是第三个 Frenet 向量 e 3 ( t ) ， 总是正交于 t 点的 单位 切向量和单位法向量。其定义为

在 3 维空间中等式简化为

挠率

第二广义曲率 χ 2 ( t ) 称为 挠率 ，度量了 γ 和一条平面曲线的偏离程度。或者说，如果挠率为 0 则曲线完全在某平面内（任何 t 都在这一个平面内）。

称为 γ 在点 t 的挠率。

曲线论主要定理

给定 n 个函数

满足

那么存在 惟一的 （在差一个欧几里得群作用的意义下） n 阶正则 C -曲线 γ，具有如下性质

这里集合

是曲面的 Frenet 标架。

再附加起始 t 0 ∈ I ，起始点 p 0 ∈ R 以及一个初始正交标架 { e 1 , ..., e n -1 } 满足

那么我们可以排除欧几里得作用得到惟一的曲线 γ。

Frenet-Serret 公式

Frenet-Serret 公式是一组一阶常微分方程。其解为由广义曲率函数 χ i 所刻画的曲线的 Frenet 向量组。

2-维

3-维

n 维一般公式

参考文献

Erwin Kreyszig, Differential Geometry , Dover Publications, New York, 1991, ISBN 9780484667218. Chapter II is is a classical treatment of Theory of Curves in 3-dimensions.

陈维桓，微分几何，北京大学出版社，北京，2006年，ISBN 7-301-10709/O.0696.

另见

曲线论题列表

曲线的仿射几何

弧

切线、切点、次切距

密切圆

包络线、转迹线

四顶点定理

测地线

等周问题

环绕数

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。