隐函数定理-族谱新闻-族谱网

隐函数定理

2020-10-16

出处：族谱网

作者：阿族小谱

浏览:227次

转发:0次

评论:0

例子定义了函数f(x,y)=x2+y2{displaystylef(x,y)=x^{2}+y^{2}}之后，单位圆就可以写成满足f(x,y)=1{displaystylef(x,y)=1}的点的集合。在圆上的每一点，比如点A上，y都可以表示成关于x的函数y(x)=1−−-->x2{displa

例子

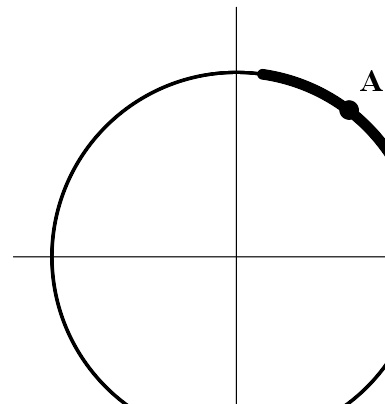
定义了函数f(x,y)=x2+y2{\displaystyle f(x,y)=x^{2}+y^{2}}之后，单位圆就可以写成满足f(x,y)=1{\displaystyle f(x,y)=1}的点的集合。在圆上的每一点，比如点A上，y都可以表示成关于x的函数y(x)=1− − -->x2{\displaystyle y(x)={\sqrt {1-x^{2}}}},除了点B以外。

定义函数f(x,y)=x2+y2{\displaystyle f(x,y)=x^{2}+y^{2}}，那么方程f(x,y)=1{\displaystyle f(x,y)=1}的所有解的集合构成单位圆（{(x,y)|f(x,y)=1}={(x,y)|x2+y2=1}{\displaystyle \{(x,y)|f(x,y)=1\}=\{(x,y)|x^{2}+y^{2}=1\}}）。圆上的点是无法用统一的方法表示成y=g(x){\displaystyle y=g(x)}的形式的，因为每个x∈ ∈ -->(− − -->1,1),{\displaystyle x\in (-1,1),}都有两个y{\displaystyle y}的值与之对应，即± ± -->1− − -->x2{\displaystyle \pm {\sqrt {1-x^{2}}}}。

然而，局部地用x{\displaystyle x}来表示y{\displaystyle y}是可以的。给定圆上一点(x,y){\displaystyle (x,y)}，如果y>0{\displaystyle y>0}，也就是说这点在圆的上半部分的话，在这一点附近y{\displaystyle y}可以写成关于x{\displaystyle x}的函数：y=1− − -->x2{\displaystyle y={\sqrt {1-x^{2}}}}。如果y<0{\displaystyle y1− − -->x2{\displaystyle y=-{\sqrt {1-x^{2}}}}。

但是，在点(1,0){\displaystyle (1,0)}的附近，y{\displaystyle y}无法写成关于x{\displaystyle x}的函数，因为(1,0){\displaystyle (1,0)}的每一个邻域中都包含了上半圆和下半圆的点，于是对于附近的每一个x{\displaystyle x}，都有两个y{\displaystyle y}的值与之对应。

定理的叙述：欧几里得空间的情况

设f : R → R为一个连续可微函数。这里R被看作是两个空间的直积：R×R，于是R中的一个元素写成 (x,y) = (x1, ..., xn, y1, ..., ym)的形式。

对于任意一点(a,b) = (a1, ..., an, b1, ..., bm)使得f(a, b) = 0，隐函数定理给出了能否在(a,b)附近定义一个y关于x的函数g，使得只要：f(x,y)=0，就有y = g( x )的充分条件。这样的函数g存在的话，严格来说，就是说存在a和b的邻域U和V，使得g的定义域是：g : U → V，并且g的函数图像满足：

隐函数定理说明，要使的这样的函数g存在，函数f{\displaystyle f}的雅可比矩阵一定要满足一定的性质。对于给定的一点 (a,b)，f{\displaystyle f}的雅可比矩阵写作：

其中的矩阵X{\displaystyle X}是f{\displaystyle f}关于x{\displaystyle x}的偏微分，而Y{\displaystyle Y}是f{\displaystyle f}关于y{\displaystyle y}的偏微分。隐函数定理说明了：如果Y{\displaystyle Y}是一个可逆的矩阵的话，那么满足前面性质的U{\displaystyle U}、V{\displaystyle V}和函数g{\displaystyle g}就会存在。概括地写出来，就是：

设f : R → R为连续可微函数，并令R中的坐标记为 (x, y)。给定一点 (a1,...,an,b1,...,bm) = (a,b)使得f(a,b)=c，其中c∈ R。如果矩阵[(∂fi/∂yj)(a,b)]是可逆矩阵的话，那么存在a的邻域U、b的邻域V以及同样是连续可微的函数g:U → V，满足{(x,g(x))}={(x,y)|f(x,y)=c}∩ ∩ -->(U× × -->V).{\displaystyle \{(\mathbf {x} ,g(\mathbf {x} ))\}=\{(\mathbf {x} ,\mathbf {y} )|f(\mathbf {x} ,\mathbf {y} )=\mathbf {c} \}\cap (U\times V).}

一般情形

设E1{\displaystyle E_{1}}、E2{\displaystyle E_{2}}和F{\displaystyle F}是三个巴拿赫空间，而U{\displaystyle U}、V{\displaystyle V}分别是E1{\displaystyle E_{1}}、E2{\displaystyle E_{2}}上的两个开集。设函数：

是一个Ck{\displaystyle C^{k}}的函数（见光滑函数），其中k≥ ≥ -->1{\displaystyle k\geq 1}，并且对于E1× × -->E2{\displaystyle E_{1}\times E_{2}}中的一点(x0,y0){\displaystyle (x_{0},y_{0})}，满足：

那么有如下结论：

存在x0{\displaystyle x_{0}}的邻域U0⊂ ⊂ -->U{\displaystyle U_{0}\subset U}以及y0{\displaystyle y_{0}}的邻域V0⊂ ⊂ -->V{\displaystyle V_{0}\subset V}；

存在一个Ck{\displaystyle C^{k}}的函数：φ φ -->:U0→ → -->V0{\displaystyle \varphi :U_{0}\rightarrow V_{0}}，使得对任意(x,y)∈ ∈ -->U0× × -->V0{\displaystyle (x,y)\in U_{0}\times V_{0}}，只要f(x,y)=0{\displaystyle f(x,y)=0}，就有

参见

反函数定理

不动点定理

压缩映射定理

微分

参考来源

（英文）Arne Hallam.The implicite function theorem(PDF). Iowa State University.

Chiang, Alpha C. Fundamental Methods of Mathematical Economics 3rd. McGraw-Hill. 1984.

Danilov, V.I.,Implicit function (in algebraic geometry), (编) Hazewinkel, Michiel,数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4 .

Edwards, Charles Henry. Advanced Calculus of Several Variables. Mineola, New York: Dover Publications. 1994 [1973]. ISBN 978-0-486-68336-2.

Fritzsche, K.; Grauert, H.From Holomorphic Functions to Complex Manifolds. Springer. 2002.

Jittorntrum, K. An Implicit Function Theorem. Journal of Optimization Theory and Applications. 1978, 25 (4). doi:10.1007/BF00933522.