理论方程形式

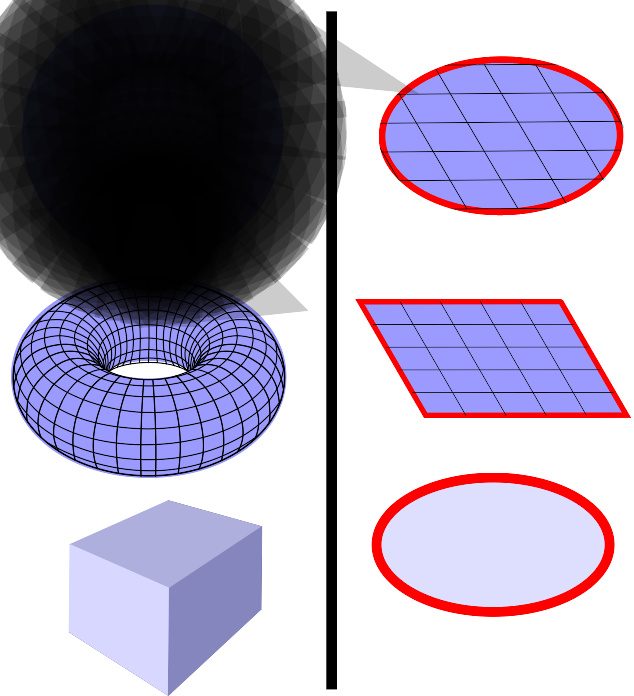
闭曲面与开放曲面示意图。左边是闭曲面例子，包括球面、环面和立方体面；穿过这些曲面的磁通量等于零。右边是开放曲面，包括圆盘面、正方形面和半球面；都具有边界（以红色显示），不完全围入三维体积。穿过这些曲面的磁通量不一定等于零。

高斯磁定律的方程可以写为两种形式：微分形式和积分形式。根据散度定理，这两种形式为等价的。

高斯磁定律的微分形式为

其中， B {\displaystyle \mathbf {B} \,\!} 是磁场。

这是麦克斯韦方程组中的一个方程。

高斯磁定律的积分形式为

其中， S {\displaystyle \mathbb {S} \,\!} 是一个闭曲面， d a {\displaystyle \mathrm {d} \mathbf {a} \,\!} 是微小面积分（请参阅曲面积分）。

这方程的左手边项目，称为通过闭曲面的净磁通量。高斯磁定律阐明这净磁通量永远等于零。

磁矢势

根据亥姆霍兹分解（ Helmholtz decomposition ），因为磁场的散度等于零，必定存在有矢量场 A {\displaystyle \mathbf {A} \,\!} 满足条件

这矢量场 A {\displaystyle \mathbf {A} \,\!} 称为 磁矢势 。

请注意并不是只有一个矢量场 A {\displaystyle \mathbf {A} \,\!} 满足这条件。实际上，有无限多个解答。应用一项矢量恒等式，

给予任意函数 ϕ ϕ --> {\displaystyle \phi \,\!} ，那么， A = A + ∇ ∇ --> ϕ ϕ --> {\displaystyle \mathbb {A} =\mathbf {A} +\nabla \phi \,\!} 也是一个解答。磁矢势的自由特性，称为规范自由。

磁场线

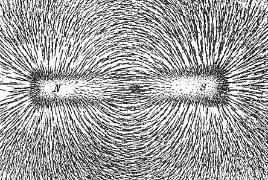
透过铁粉显示出的磁场线。将条状磁铁放在白纸下面，铺洒一堆铁粉在白纸上面，这些铁粉会依著磁场线的方向排列，形成一条条的曲线，在曲线的每一点显示出磁场线的方向。

磁场，就像任何矢量场，可以用场线来描绘其轨迹。磁场线是一组曲线，其方向对应于磁场的方向，其面密度与磁场的大小成正比。因为磁场的散度等于零，磁场线没有初始点，也没有终结点。磁场线或者形成一个闭循环，或者两个端点都延伸至无穷远。

磁单极子

假若，有科学家发现磁单极子存在于宇宙，则高斯磁定律不正确，必须修正。磁场的散度会与磁荷密度 ρ ρ --> m {\displaystyle \rho _{m}\,\!} 成正比 ：

其中， μ μ --> 0 {\displaystyle \mu _{0}\,\!} 是磁常数。

毕奥-萨伐尔定律

从毕奥-萨伐尔定律，可以推导出高斯磁定律。毕奥-萨伐尔定律阐明，设定电流密度 J ( r ′ ) {\displaystyle \mathbf {J} (\mathbf {r} ")\,\!} ，则磁场为

其中， r ′ {\displaystyle \mathbf {r} "\,\!} 是源位置， r {\displaystyle \mathbf {r} \,\!} 是场位置， V ′ {\displaystyle \mathbb {V} "\,\!} 是积分的体积， d 3 r ′ {\displaystyle d^{3}r"\,\!} 是微小体积元素。

应用一项矢量恒等式，

将这恒等式带入毕奥-沙伐方程。由于梯度只作用于无单撇号的坐标，可以移到积分外，改为旋度：

应用一项矢量恒等式，

所以，高斯磁定律成立：

参阅

磁矩

安培力定律

毕奥-萨伐尔定律

电磁场的数学表述

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。