更多文章
更多精彩文章

数值解
杜芬方程没有解析解,但可用龙格-库塔法求得数值解。
当γ>0,杜芬振子呈现极限环振动;
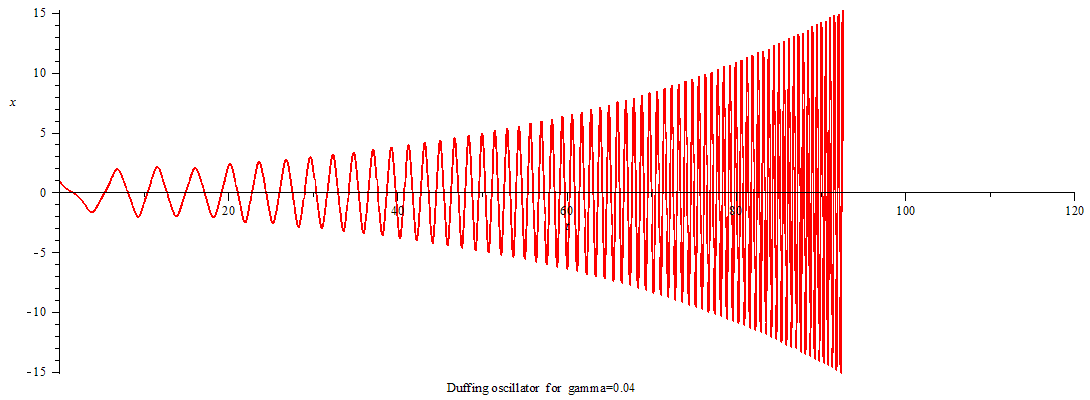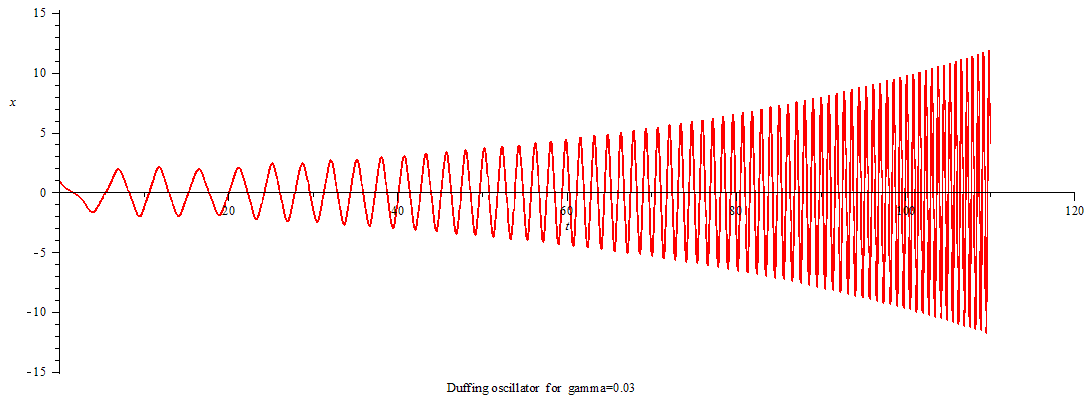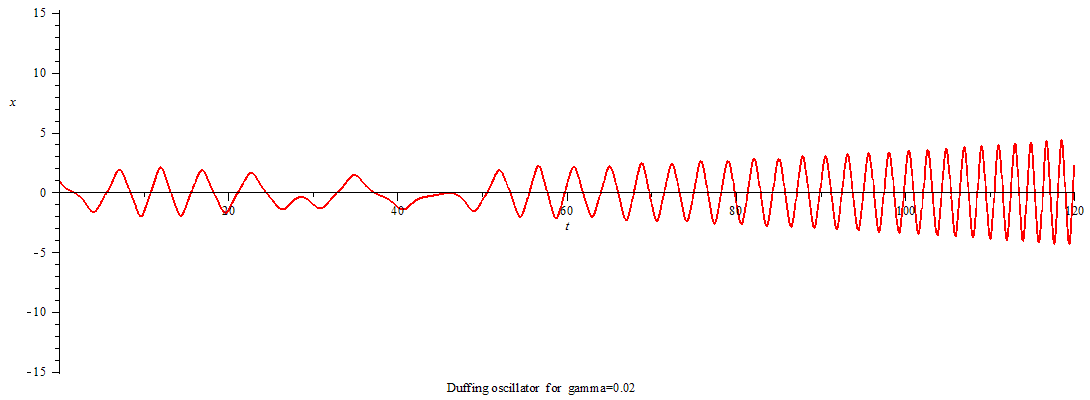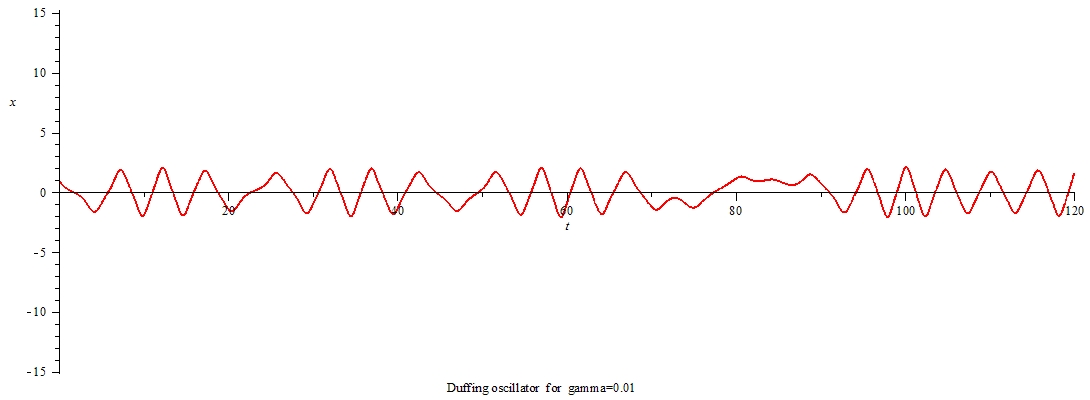
Duffing oscillator limit cycle
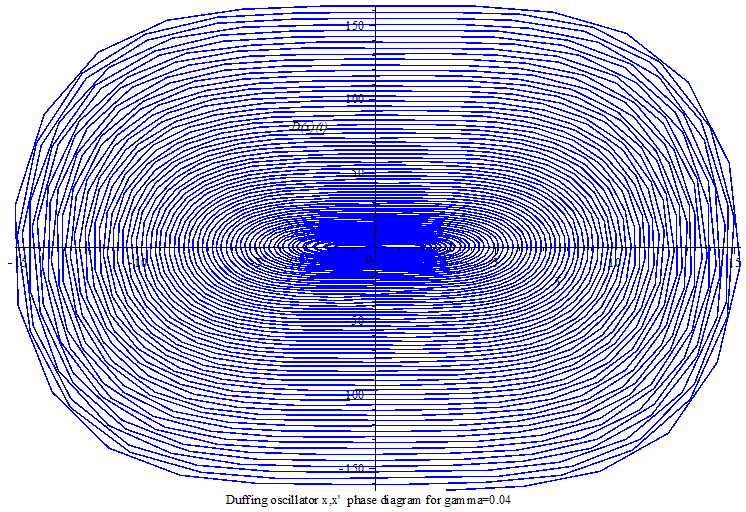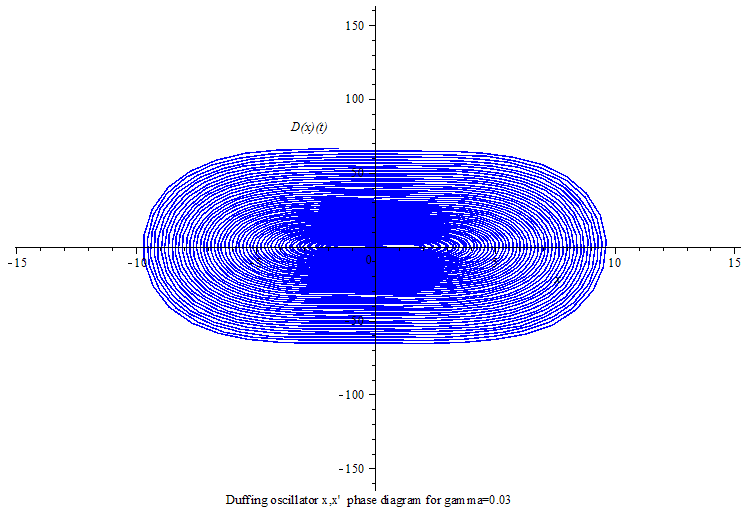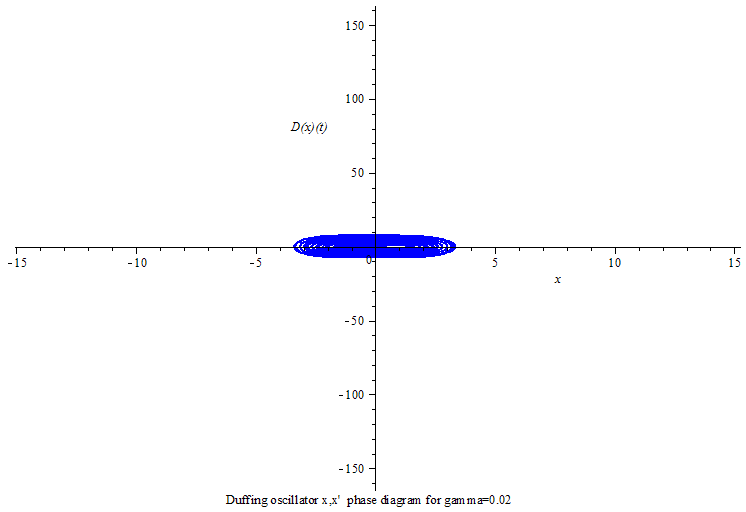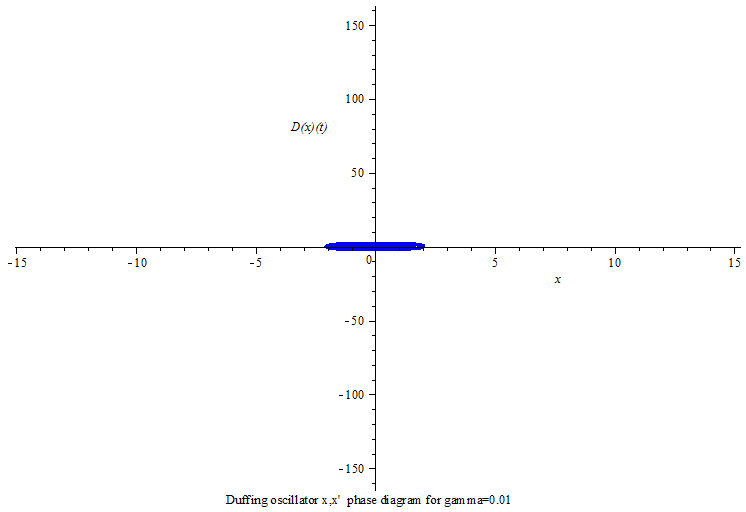
Duffing oscillator limit cycle phase animation
当γ<0,系统进入混沌态,相图呈吸引子形态。
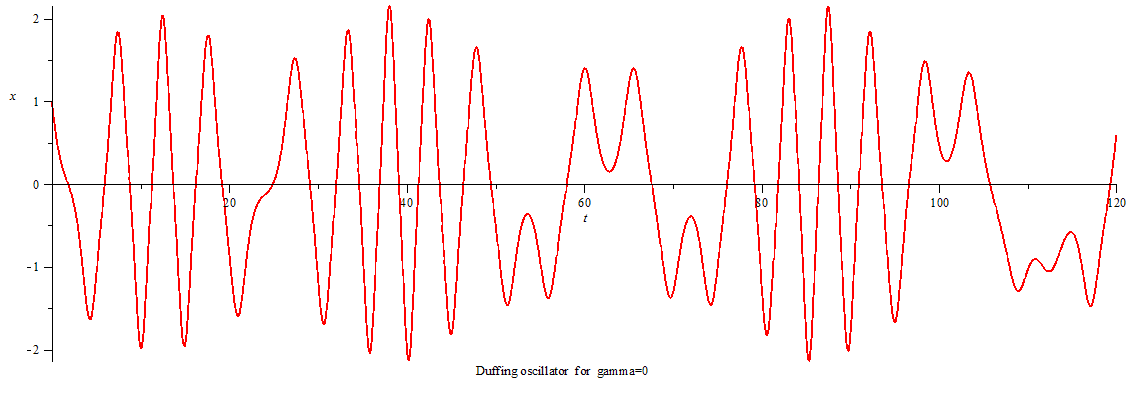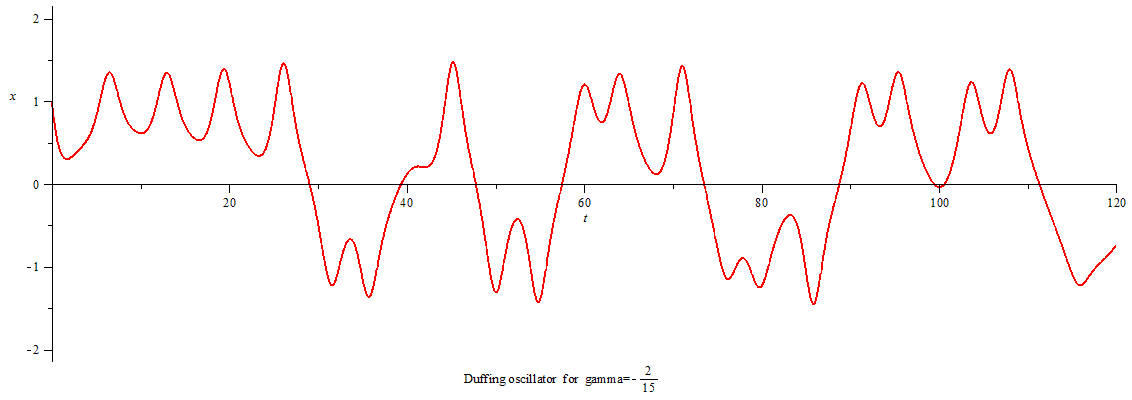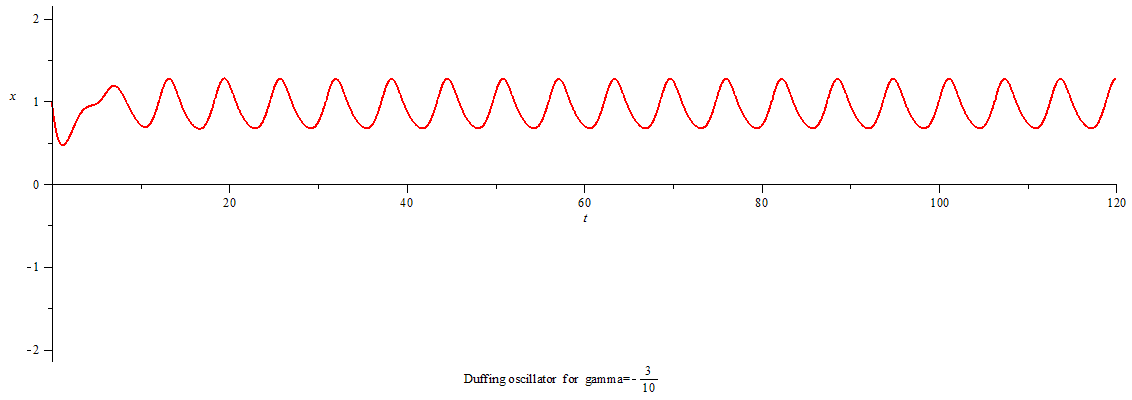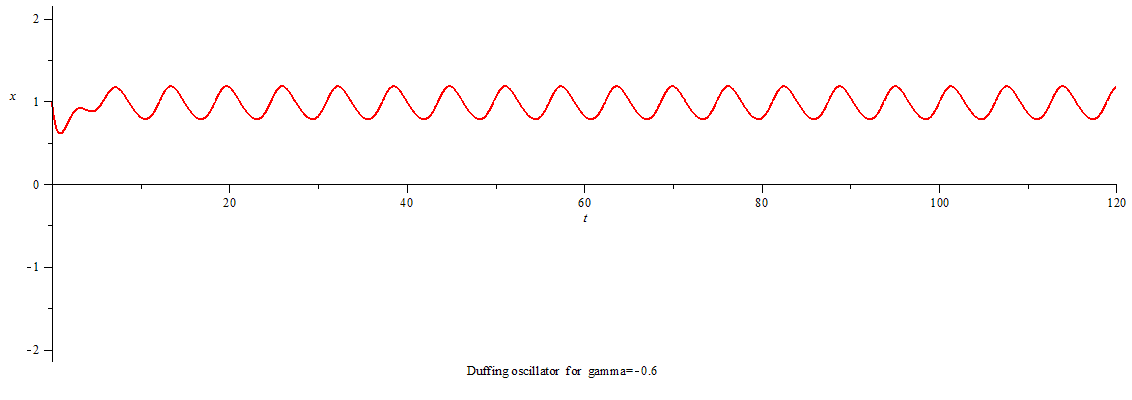
Duffing oscillator chaos

Duffing oscillator attractors animation
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。













{{item.time}} {{item.replyListShow ? '收起' : '展开'}}评论 {{curReplyId == item.id ? '取消回复' : '回复'}}