莫塞莱定律
历史
应用 1910 年代的X-射线衍射科技,亨利·莫塞莱发现一个元素的 X-射线谱内,强度最高的短波长谱线,与元素的原子序数 Z{\displaystyle Z\,\!} 有关。他辨明这条谱线为 K-α 谱线,并且发现这关系可以用一个简单的公式表达,后来称为莫塞莱定律 :
其中,ν ν -->{\displaystyle \nu \,\!} 是频率,主谱线壳层K壳层X-射线发射谱线的频率,k1{\displaystyle k_{1}\,\!} 和 k2{\displaystyle k_{2}\,\!} 是依不同种类的谱线而设定的常数。
例如,每一条 K-α 谱线(西格巴恩标记 (Siegbahn notation))都有相同的 k1{\displaystyle k_{1}\,\!} 和 k2{\displaystyle k_{2}\,\!} 值。所以,公式可以重写为
莫塞莱本人选择不用 k1{\displaystyle k_{1}\,\!} ,而采用标准里德伯格式来表达。根据里德伯公式,K-α 谱线的 k1{\displaystyle k_{1}\,\!} 是 1− − -->1/4=3/4{\displaystyle 1-1/4=3/4\,\!} 乘以里德伯频率(3.29∗ ∗ -->1015{\displaystyle 3.29*10^{15}\,\!} )。L-α 谱线的 k1{\displaystyle k_{1}\,\!} 是 1/4− − -->1/9=5/36{\displaystyle 1/4-1/9=5/36\,\!} 乘以里德伯频率。
莫塞莱的 k2{\displaystyle k_{2}\,\!} 值是一个一般性实验常数,专门用来配合 K-α 跃迁谱线或 L-α 跃迁谱线(后面系列谱线的强度比较弱,频率比较低,修正 Z{\displaystyle Z\,\!} 的 k2{\displaystyle k_{2}\,\!} 值比较大)。莫塞莱计算出 L-α 跃迁的整个项目是 (Z− − -->7.4)2{\displaystyle (Z-7.4)^{2}\,\!} ,与实验数据的配合相当接近。K-α 谱线的配合更接近,其 k2{\displaystyle k_{2}\,\!} 值是 1{\displaystyle 1\,\!} 。
这样,采用原本里德伯格式标记,莫塞莱的 K-α 谱线和 L-α 谱线的公式可以表达为:
本来,莫塞莱很可能会因为莫塞莱定律的重大贡献而得到诺贝尔物理奖。1914 年,第一次世界大战爆发,莫塞莱自愿入伍从军。很不幸地,1915 年,战死于加里波利之战,年仅 27 岁。
导引与论证
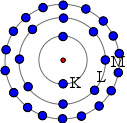
原子的 K 、L 、M 电子层,和它们最多能够容纳的电子数目。
1913 年,从点绘 X-射线频率的平方根 对 原子序数的曲线,莫塞莱找到了他的经验公式。同年,尼尔斯·玻尔也发表了玻尔模型。很快地,于 1914 年,莫塞莱发觉,假若能再加入一些关于原子结构的合理的额外假设,就可以用玻尔模型来解释他的公式。可是,在莫塞莱找到他的公式那时,他和玻尔都无法给出假设的形式。
用玻尔模型解释,十九世纪经验导引出来的里德伯公式,描述了氢原子的电子从一个能级移至另一个能级的跃迁行为。在这同时,一个光子被发射出来。从这几个能级的数值,可以求出来氢原子发射的光子的频率。
根据玻尔模型,假设最初能级大于最终能级,氢原子发射的光子的频率乘以普朗克常数,等于最初能级减去最终能级的差值。采用普朗克单位制,经过一番运算,可以得到里德伯公式的玻尔形式,称为玻尔公式:
其中,h{\displaystyle h\,\!} 是普朗克常数,me{\displaystyle m_{e}\,\!} 是电子的质量,qe{\displaystyle q_{e}\,\!} 是电子的电荷量( − − -->1.60× × -->10− − -->19{\displaystyle -1.60\times 10^{-19}\,\!}库仑),qZ=Zqe{\displaystyle q_{Z}=Zq_{e}\,\!} 是原子核的电荷量,ϵ ϵ -->0{\displaystyle \epsilon _{0}\,\!} 是真空电容率,nf{\displaystyle n_{f}\,\!} 是最终能级量子数,ni{\displaystyle n_{i}\,\!} 是最初能级量子数。
1914 年,莫塞莱发觉,给予两个假设,他可以从玻尔公式里改写出他的公式。第一个假设是,每一个原子光谱的最明亮的谱线 ( K-α 谱线),是由电子从 L 壳层跃迁至 K 壳层的同时发射出的谱线。 L 壳层和 K 壳层的能量量子数分别为 2 和 1 。第二个假设是,在玻尔公式里的 Z{\displaystyle Z\,\!} 必须减去 1 ,才能正确地计算出 K-α 谱线(许多年以后,物理学家了解这修正乃由屏蔽效应(screening effect) 所造成的。首先,原子 K 壳层内两个电子中间的一个电子被散射出原子。这造成了 K 壳层内有一个空位.立刻,在其它壳层,能级较高的电子会跃迁入这空位,因而发射出能量等于能级差值的射线。这能级差值与屏蔽效应有关。整个原子核的单位电荷数目 Z{\displaystyle Z\,\!} 被 K 壳层剩余的电子所屏蔽。由于在这过程中, K 壳层只有一个 {\displaystyle \,\!} 电子,原子核的有效单位电荷数目是 Z− − -->1{\displaystyle Z-1\,\!} )。这样,莫塞莱的 K-α 谱线的玻尔公式成为
所以,频率是
这答案的 2.48∗ ∗ -->1015{\displaystyle 2.48*10^{15}\,\!} Hz 与莫塞莱的实验得到的结果 2.47∗ ∗ -->1015{\displaystyle 2.47*10^{15}\,\!} Hz 相吻合。这个基本频率与氢原子来曼-α谱线的频率相同。因为,氢原子的 {\displaystyle \,\!} 至 2p{\displaystyle 2p\,\!} 跃迁是来曼-α 谱线和 K-α 谱线的物理机制。莫塞莱很清楚地知道,他的基本频率是莱曼-α 谱线频率。他也很有把握地断定,原子核最内层的 K 壳层只能容纳两个电子。
但是,对于较重元素(铝以上)的 K-α 谱线,原子序数 Z{\displaystyle Z\,\!} 减去 1 的必要,完全是由莫塞莱从实验中得到的。在论文中,他并没有讨论到任何理论方面的问题,因为在 1913 年,电子层和其原子轨域的观念,还没有稳固地建立起来。特别地,一直到 1926 年以前,薛定谔方程和其计算出来的轨域,包括 {\displaystyle \,\!} 轨域和其两个电子,都还没有被正式提出及完全了解。在 1913 年,莫塞莱和玻尔都被这 Z− − -->1{\displaystyle Z-1\,\!} 项目的物理诠释深深地困惑著。
至于莫塞莱的 L-α 跃迁,现代的观点给予每一个电子层一个主量子数 n{\displaystyle n\,\!} 。假若电子层的主量子数是 n{\displaystyle n\,\!} ,则这电子层可以包含 2n2{\displaystyle 2n^{2}\,\!} 个电子。这样, n=1{\displaystyle n=1\,\!} 壳层有两个电子;而 n=2{\displaystyle n=2\,\!} 壳层则有八个电子。L-α 跃迁是从 M 壳层跃迁至 L 壳层。而 K 壳层和 L 壳层总共可容纳十个电子。莫塞莱的 K2{\displaystyle K_{2}\,\!} 的实验值是 7.4 ,应该是电子的屏蔽效应所造成的。
历史重要性
莫塞莱公式不只建立了原子序是一个可测量的实验数值,而且还给予了原子序一个物理意义,那就是,原子序是原子核的单位电荷数目(后来的科学家发觉是质子数目)。因为莫塞莱对于 X-射线的研究成果,在周期表,可以依照原子序来排列各个元素,而不是依照原子量。这个新的排列方法使得镍元素( Z=28,58.7amu{\displaystyle Z=28,58.7amu\,\!} )与钴元素( Z=27,58.9amu{\displaystyle Z=27,58.9amu\,\!} )的排列位置相互对易。
这研究成果也使得科学家能够计算出谱线的数值方面的预测,核对半量子的玻尔模型。根据玻尔模型,从一个能级跃迁到另一个能级的能量差值,可以用来计算,在周期表内,从铝元素到金元素的 X-射线谱线,而且这些计算结果确实地跟原子序有关。这事实使得卢瑟福/玻尔派的原子论得到广泛的接受。后来发展成功的量子理论基本上也得回了玻尔公式的谱线能量。莫塞莱定律被并入整个量子力学的原子观。在一个 K 壳层电子被弹出后,单独剩余在 K 壳层的另一个 {\displaystyle \,\!} 电子所扮演的角色,可以用薛定谔方程给予完整地合理解释。
参阅
玻尔模型
卢瑟福散射
弗兰克-赫兹实验
参考文献
牛津大学物理教学 – 历史档案, "展览 12 - 莫塞莱的曲线图" 复制的莫塞莱曲线图,显示出频率的平方根相关性。
Whitaker, M A B. The Bohr-Moseley synthesis and a simple model for atomic x-ray energies. European Journal of Physics. May 1999, 20 (3): pp.213–220. doi:10.1088/0143-0807/20/3/312. 引文格式1维护:冗余文本 (link) 对于莫塞莱的屏蔽效应分析,作者 M A B Whitake 在这篇论文里,有详尽的评论。
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。

- 有价值
- 一般般
- 没价值








24小时热门
推荐阅读
知识互答
关于我们

APP下载


























{{item.time}} {{item.replyListShow ? '收起' : '展开'}}评论 {{curReplyId == item.id ? '取消回复' : '回复'}}